модели тренда параметров тренда

10. Запомнить (или записать в конспект) величину R² = 0,8871 для линейной модели.

11. Запомнить (записать) значение R² = 0,8467 для логарифмической модели.

12. Повторить п. 10 и 11 для других типов тренда: Полиномиальная (по умолчанию применяется полином 2 степени), Степенная и Экс­поненциальная, за исключением Линейная фильтрация.

13. Лучшим в нашем примере является тренд типа Экспоненци­альная, т.к. его величина (R² = 0,9519) является максимальной среди ос­тальных.

Величина R² является критерием выбора наилучшего типа тренда, наиболее подходящего к анализируемым данным. Чем ближе его значение приближается к 1, тем лучше выбранная модель тренда подходит для вы­ражения тенденций исследуемых данных.

14. Полученное уравнение регрессии можно увидеть на диаграмме в верхнем правом углу (рис. 24). Уравнение имеет вид: у = 50,169 е ^0.0009х.

Полученное уравнение регрессионной зависимости можно использо­вать в дальнейшем для решения некоторых задач прогнозирования. На­пример, задавшись известным значением независимой переменной X (ко­личество безработных) и подставив его в найденное уравнение регрессии, можно рассчитать неизвестное значение зависимой переменной - Y (коли­чество преступлений).

15. Для определения прогнозных значений преступности на 2011 г. используем уравнение полученной регрессии: у = 50,169 е ^0.0009х , где y - ко­личество преступлений,
а х - количество безработных.

16. Используя технологию подстановки независимой переменной в уравнение, описанную выше, подставим вместо х- 1850, получим искомое значение преступности - 265 преступлений (в строке формул: f_x =50,169*ЕХР(0 0009*1850)).

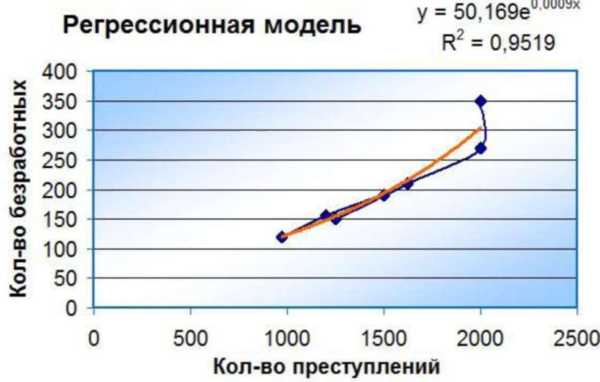
Рис. 24. Регрессионная модель зависимости между количеством безработных и количеством преступлений

Таким образом, в результате прогнозирования методом моделирова­ния (на основе регрессионной модели) количество преступлений в 2011 г. составит число 265.

Безусловно, такой способ прогнозирования на основе простой рег­рессии, без совместного применения с другими способами, может иметь значительную ошибку. Но для уточнения прогнозных значений некоторых переменных, полученных методом экстраполяции, в случае изменения факторов внешней среды на прогнозном горизонте, он может быть исполь­зован достаточно эффективно