Использование таблиц с постоянным шагом

Наиболее простой вид принимают формулы численного дифференцирования при использовании таблиц y_i=f(x_i) с постоянным шагом. В тех случаях, когда значение производной необходимо вычислять в крайних для таблицы точках x₀ и x_n, используются односторонние формулы численного дифференцирования 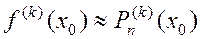и .

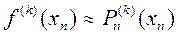Например, при n=2, дифференцируя многочлен Ньютона, получим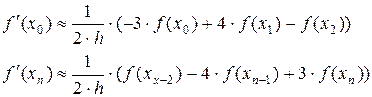

имеющие второй порядок точности.

Другие подходы

Применение формулы (13) для вычисления производной f^(k) фактически основано на кусочно-полиномиальной интерполяции. Полученная таким образом производная в точке «стыка» двух соседних многочленов может иметь разрыв. Поэтому, если требуется глобально на отрезке [a, b] аппроксимировать производную гладкой функцией, то целесообразно использовать сплайны.

Сплайном называется функция, которая вместе с несколькими производными непрерывна на всем заданном отрезке [a, b], а на частичном отрезке [x_i, x_i+1] в отдельности является некоторым алгебраическим многочленом. При этом отрезок [a, b] разбит на N равных частичных отрезков [x_i, x_i+1], где x_i=a+ih, i=0,1,...,N-1, x_N=b, h=(b-a)/N.

Максимальная по всем частичным отрезкам степень многочленов называется степенью сплайна, а разность между степенью сплайна и порядком наивысшей непрерывной на [a, b] производной – дефектом сплайна.

Производная 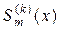сплайна 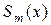при 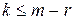, где r- дефект сплайна, дает гладкую глобальную аппроксимацию для .

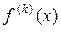Когда значения функции сильно «зашумлены» случайными ошибками, полезным может оказаться использование метода наименьших квадратов.