Интерполяции алгебраическими многочленами

Пусть P_n(x) – интерполяционный многочлен степени n с узлами интерполяции 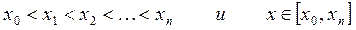. В этом случае формула (12) принимает вид 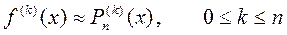(13)

При этом справедлива оценка погрешности формулы (13) 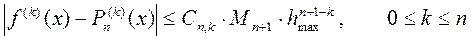(14),

где С_n,k - положительные числа,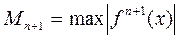

Замечание 1.

Порядок точности формулы (13) относительно h_max равен разности между числом узлов интерполяции и порядком вычисляемой производной.

Замечание 2.

Если формулы (13) применяется для вычисления производной в точке, относительно которой узлы таблицы расположены симметрично, и число n-k четно, то порядок точности формулы повышается на единицу по сравнению с порядком n+1-k, который гарантирует оценка (14). Таковы, например, формулы (6), (8), (9), (11).

Из формулы интерполяционного многочлена Ньютон следует, что .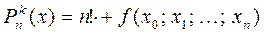

Таким образом, справедлива приближенная формула 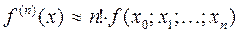, (15)

имеющая, по крайней мере, один первый порядок точности.

/*Формула (15) следует из свойства разделенных разностей, а именно: функция f имеет на отрезке [a,b] , содержащем точки x_i,x_i+1,...,x_i+k производную порядка k. Тогда справедливо равенство 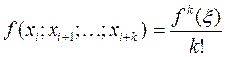, где 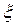- некоторая точка, расположенная на (a, b)*/

Частным случаем формулы (15) является формулы: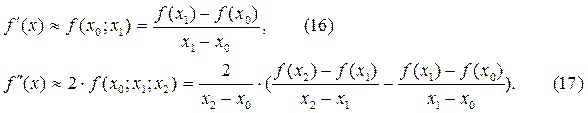

При выборе в качестве узлов интерполяции значений x₀=x, x₁=x+h формула (16) превращается в формулу (1). При выборе x₀=x-h, x₁=x из (16) получается (2), а при x₀=x-h, x₁=x+h – формула (6). Аналогично из формулы (17) получается формула (9).