Определение расчетной нагрузки

Вся нагрузка, действующая на ферму, обыч­но прикладывается к узлам фермы, к которым прикрепляются элементы поперечной конструкции (например, прогоны кровли или подвесного потолка), передающие на­грузку на ферму. Если нагрузка приложена непосредственно в панели, то в основной расчетной схеме она также распределяется между ближайшими узлами, но дополни­тельно учитывается местный изгиб пояса от расположенной на нем нагрузки. Пояс фермы при этом рассматривается как неразрезная балка с опорами в узлах.

Рекомендуется определять усилия в стержнях ферм отдельно для каждого вида на­грузки. Так, в стропильных фермах усилия следует определять для следующих нагрузок:

- постоянной, в которую входит собственная масса фермы и всей поддерживаемой конструкции (кровли с утеплением, фонарей и т.п.);

- временной - нагрузки от подвесного подъемно-транспортного оборудования, по­лезной нагрузки, действующей на подвешенное к ферме чердачное перекрытие, и т.п.;

- кратковременной (например, атмосферной) - снег, ветер.

Расчетная постоянная нагрузка, действующая на любой узел стропильной фермы, зависит от грузовой площади, с которой она собирается (заштрихована на рис. 8.13), и определяется по формуле

F_gi = (g _ф + g _кр /cosα)b[(d_i-1 + d_i)/2) γ_g], (8.2)

где g _ф - собственная масса фермы и связей, кН/м², горизонтальной проекции кровли; g_кр - масса кровли, кН/м²; α - угол наклона верхнего пояса к горизонту; b - рассто­яние между фермами; d_i-1 и d_i - примыкающие к узлу панели; γ_g - коэффициент надежности для постоянных нагрузок.

В отдельных узлах к нагрузке, получаемой по формуле (8.2), прибавляется нагрузка от массы фонаря.

Снег - нагрузка временная, она может загружать ферму лишь частично. Загружение снегом одной половины фермы может ока­заться невыгодным для средних раскосов.

Расчетную узловую нагрузку от снега определяют по формуле

F_si= S_g b[(d_i-1 + d_i)/2)], (8.3)

где S_g - масса снегового покрова на 1 м² горизонтальной проекции кровли.

Значение S_g должно определяться с учетом возможного неравномерного рас­пределения снегового покрова около фо­нарей или перепадов высот.

Давление ветра учитывается только на вертикальные поверхности, а также на по­верхности с углом наклона к горизонту более 30°, что бывает в башнях, мачтах, эстакадах, а также в крутых треугольных стропильных фермах и фонарях. Ветровая нагрузка, как и другие виды нагрузок, приводится к узловой. Горизонтальная на­грузка от ветра на фонарь при расчете стро­пильной фермы, как правило, не учиты­вается, так как ее влияние на работу фер­мы незначительно.

8.4.2. Определение усилий в стержнях ферм.При расчете ферм со стержнями из уголков или тавров предполагается, что в узлах системы - идеальные шарниры, оси всех стержней прямолинейны, расположены в одной плоскости и пересекаются в цент­рах узлов (рис. 9.3). Стержни такой идеальной системы работают только на осевые усилия: напряжения найденные по этим усилиям, являются основными. В связи с факти­ческой жесткостью узловых соединений в стержнях фермы возникают дополнительные напряжения, которые при отношении высоты сечения стержня к его длине h/l<1/15 расчетом не учитываются, так как они мало влияют на несущую способность конструкции.

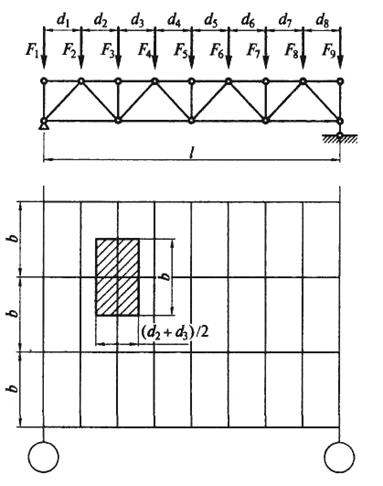
Рис. 8.13. Расчетная схема фермы

В фермах со стержнями, имеющими повышенную жесткость на изгиб, влияние же­сткости соединений в узлах более значительно. Кроме того, моменты в узлах приводят к более раннему возникновению пластических деформаций в сечениях элементов, что снижает хрупкую прочность стали. Поэтому для двутавровых, трубчатых и Н-образных сечений стержней расчет ферм по шарнирной схеме допускается при отношении высо­ты сечения к длине не более 1/10 для конструкций, эксплуатируемых при расчетной температуре ниже -40°С. При превышении этих отношений следует учитывать допол­нительные изгибающие моменты в стержнях от жесткости узлов. При этом осевые уси­лия можно определять по шарнирной схеме, а дополнительные моменты определять приближенно.

В верхних поясах ферм при непрерывном опирании на них настилов (равномерное распределение нагрузки на поясе фермы) допускается вычислять моменты по следую­щим формулам:

пролетный момент в крайней панели

М₁ = qd₁²/10; (8.4)

пролетный момент промежуточных панелей

М_i = qd₁²/12; (8.5)

момент в узле (опорный)

М_оп = qd₁²/18, (8.6)

где q - распределенная нагрузка на ферму; d - длина панели.

Кроме того, в стержнях фермы возникают напряжения от моментов в результате неполного центрирования стержней в узлах. Эти напряжения, не являющиеся основ­ными, как правило, расчетом не учитываются, так как допускаемые в фермах эксцен­триситеты малы и незначительно влияют на их несущую способность.

Смещение оси поясов ферм при изменении сечений не учитывается, если оно не превышает 1,5% высоты пояса.

Расчет ферм следует выполнять на ЭВМ, что позволяет рассчитать любую схему фермы на статические и динамические нагрузки с учетом, если надо, моментов от жесткости узлов и смещения осей стержней.

Существующие программы расчета позволяют получать расчетные усилия в стерж­нях с учетом требуемых сочетаний нагрузок и выполнять подбор сечений стержней из наиболее распространенных сварных и прокатных профилей.

Использование ЭВМ позволяет также оптимизировать конструкцию, т.е. найти оп­тимальные схему фермы, материал стержней, тип сечений, что позволяет получить наиболее экономичное проектное решение.

При отсутствии ЭВМ усилия в стержнях ферм удобнее всего определять графичес­ким методом, т.е. построением диаграмм Максвелла - Кремоны, причем для каждо­го вида нагрузки (нагрузки от покрытия, от подвесного транспорта и т.п.) строят свою диаграмму. Для ферм с несложными схемами (например, для ферм с параллель­ными поясами) и небольшим числом стержней более простым может оказаться ана­литическое определение усилий. Если фермы работают на подвижную нагрузку, то максимальные усилия в стержнях фермы от подвижной нагрузки определяют по ли­ниям влияния.

В соответствии с классификацией сочетаний нагрузок (основные и особые) усилия определяют отдельно для каждого вида сочетаний и несущую способность стержней проверяют по окончательному расчетному наибольшему усилию.

Рекомендуется результаты статического расчета записывать в таблицу, в которой должны быть приведены значения усилий от постоянной нагрузки, от возможных ком­бинаций временных нагрузок (например, от одностороннего загружения снегом), а также расчетные усилия как результат суммирования усилий при невыгоднейшем загружении для всех возможных сочетаний нагрузок.

8.4.3. Определение расчетной длины стержней.В момент потери устойчивости сжа­тый стержень выпучивается, поворачивается вокруг центров соответствующих узлов и вследствие жесткости фасонок заставляет поворачиваться и изгибаться в плоскости фермы остальные стержни, примыкающие к этим узлам (рис. 8.14).

Примыкающие стержни сопротивляются изгибу и повороту узла и этим препятству­ют свободному изгибу стержня, теряющего устойчивость. Наибольшее сопротивление повороту узла оказывают растянутые стержни, поскольку их деформация от изгиба ведет к сокращению расстояния между узлами, между тем как от основного усилия это расстояние должно увеличиваться. Сжатые же стержни слабо сопротивляются изгибу, так как деформации от поворота и осевого усилия направлены у них в одну сторону, кроме того, они могут терять устойчивость одновременно.

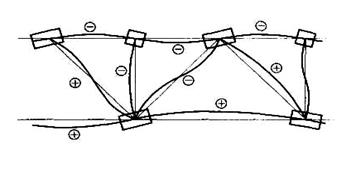
Рис. 8.14. Схема деформаций стержней при потере устойчивости сжатого стержня

Таким образом, чем больше растянутых стержней примыкает к сжатому стержню и чем они мощнее, т.е. чем больше их погонная жесткость, тем выше степень защемле­ния стержня и меньше его расчетная длина; влиянием сжатых стержней на защемление можно пренебречь.

Поэтому в качестве степени защемления сжатого стержня в узлах может быть при­нято отношение

τ = i/∑i_р, (8.7)

где i - погонный момент инерции рассматриваемого стержня в плоскости фермы; ∑i_р - сумма погонных моментов инерции растянутых стержней, примыкающих к рассматри­ваемому стержню с обоих его концов.

Чем меньше отношение τ, тем больше степень защемления и меньше расчетная длина стержня фермы

L_ef =μl, (8.8)

где μ - коэффициент приведения длины, зависящий от степени защемления; l - рас­стояние между центрами узлов.

Сжатый пояс оказывается слабо защемленным в узлах, так как с каждой стороны к нему примыкает только по одному растянутому раскосу, погонная жесткость которых значительно меньше погонной жесткости пояса. Поэтому защемлением сжатого пояса можно в запас устойчивости пренебречь и принимать его расчетную длину равной рас­стоянию между смежными узлами.

К сжатым стержням решетки в верх­нем узле примыкает растянутый раскос, а в нижнем узле - растянутые панели ниж­него пояса и раскос (рис. 8.14). Здесь степень защемления значительно больше и отношение τ получается небольшим, близким к 0,5, что дает значение коэф­фициента μ = 0,77.

По нормам коэффициент приведения длины μ элементов решетки из уголков в плоскости фермы установлен равным 0,8.

Таким образом, расчетная длина l_x = 0,8l в плоскости фермы определяется с некоторым запасом, в особенности для средних раскосов, жесткость которых по сравнению с при­мыкающими стержнями невелика.

Исключение составляет опорный восходящий раскос, условия работы которого в плос­кости фермы такие же, как и у верхнего пояса, вследствие чего расчетная длина опорно­го раскоса в плоскости фермы принимается равной расстоянию между центрами узлов.

Расчетная длина пояса в плоскости, перпендикулярной плоскости фермы, прини­мается равной расстоянию между узлами, закрепленными связями от смещения из плоскости фермы.

В беспрогонных покрытиях верхний пояс стропильных ферм закреплен в плоскости кровли жесткими плитами или панелями настила, прикрепленными к поясам ферм в каждом узле. В этом случае за расчетную длину пояса из плоскости фермы можно при­нимать ширину одной плиты.

Расчетная длина стержней решетки при выгибе их из плоскости фермы принимает­ся равной расстоянию между геометрическими центрами узлов, так как фасонки весь­ма гибки из плоскости фермы и должны рассматриваться как листовые шарниры.

В трубчатых фермах с бесфасоночными узлами расчетная длина раскоса как в плос­кости, так и из плоскости фермы с учетом повышенной крутильной жесткости замкну­тых сечений может приниматься равной 0,9l.

В других случаях расчетные длины элементов ферм принимаются по нормам.

8.4.4. Предельные гибкости стержней.Элементы конструкций, как правило, должны проектироваться из жестких стержней. Особенно существенное значение гибкость λ имеет для сжатых стержней, теряющих устойчивость при продольном изгибе.

Даже при незначительных сжимающих усилиях гибкость сжатых стержней не долж­на быть слишком большой. Очень гибкие стержни легко искривляются от случайных воздействий, провисают от собственной массы, в них появляются нежелательные экс­центриситеты, они вибрируют при динамических нагрузках. Поэтому для сжатых стер­жней устанавливается предельная наибольшая гибкость, которая является такой же нормативной величиной, как и расчетное сопротивление.

Значение предельной гибкости [λ],установленное в нормах, зависит от назначения стержня и степени его загруженности α

α = N/(φAR_γy_c), (8.9)

где N- расчетное усилие;

φAR_γy- несущая способность стержня.

Предельная гибкость стержней [λ]

Сжатые пояса, опорные стойки и раскосы ………………….………180 - 60 α

Прочие сжатые стержни ферм ………………………………… …….210- 60 α

Сжатые стержни связей............................................... ………… ….. 200

При этом αпринимается не менее 0,5.

Растянутые стержни конструкции также не должны быть слишком гибкими, так как они могут погнуться при транспортировании и монтаже.

Особенно важно, чтобы стержни имели достаточную жесткость в конструкциях, подверженных динамическим воздействиям (для предотвращения вибрации стержней).

Для растянутых стержней ферм, подвергающихся непосредственному действию ди­намической нагрузки, установлены следующие значения предельной гибкости [λ]:

Растянутые пояса и опорные раскосы............................ …………….250

Прочие растянутые стержни ферм ................................. …………….350

Растянутые стержни связей ............................................. …………….400

В конструкциях, не подвергающихся динамическим воздействиям, гибкость растя­нутых стержней ограничивают только в вертикальной плоскости (чтобы предотвратить чрезмерное их провисание), установив для всех растянутых стержней предельную гиб­кость [λ] = 400.