Устойчивость стоек со сплошными поперечными сечениями

Расчет на прочность и устойчивость стоек, работающих при центральном сжатии, производится по формуле

σ = N/F <= [σ]_р· φ. (7.5)

При введении в расчетную формулу коэффициента φ<1 обеспечивается расчетная устойчивость сжатого элемента при продоль­ном изгибе. Величина φ зависит от гибкости сжатого элемента. Гибкостью λ называют отношение свободной длины элемента L к радиусу инерции r поперечного сечения гибкого элемента:

λ=L/r. (7.6)

Радиус инерции равен:

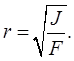(7.7)

В направлении, где радиус инерции имеет наименьшее значение, гибкость элемента наибольшая. Для конструкции, шарнирно закрепленной по концам (табл. 7.2), свободная длина L₀ прини­мается равной длине стойки L. При этом гибкость стойки определя­ется формулой (7.6). Примерами подобных конструкций могут служить элементы сжатых поясов ферм.

Таблица 7.2

Расчетные длины сжатых стержней

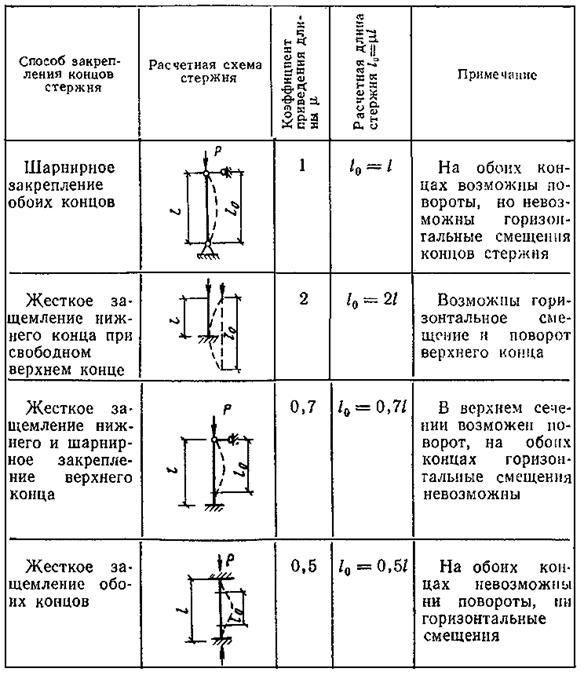
В конструкции, имеющей один конец защемленный (табл. 7.2), гибкость равна:

λ =2 L/r. (7.8)

У стоек с жестким защемлением обоих концов стержня (табл. 7.2), гибкость определяется:

λ =0,5L/r. (7.9)

Значения коэффициентов φ, установленные на основе исследований, приведены выше в табл. 7.1.

Во избежание местной потери устойчивости стенку стойки подкрепляют продольными ребрами жесткости.

Часто напряжения в сжатых элементах проверяют по преобразованной формуле

σ = N/(F·φ). (7.10)

При этом произведение F·φ называют приведенной площадью сжатого элемента.

Трудность подбора сечения сжатого элемента при заданном значении си­лы N состоит в том, что допускаемое напряжение является функцией коэф­фициента φ, а последний зависит от поперечного сечения, которое еще не подобрано. Поэтому для подбора поперечного сечения стоек пользуются методом последовательного приближе­ния. Первоначально задаются коэффициентом φ =0,5-0,8 в зависимости от рода конструкции. Можно принять среднее значение φ₁=0,65. С учетом коэффициента φ₁ определяют тре­буемую площадь поперечного сечения элемента по формуле:

F₁ = N/([σ_р] φ₁). (7.11)

Затем проектируют сечение, которое обозначим F₂, находят в нем наименьшее значение момента инерции I_min, наименьший радиус инерции r_min = √ I_min/F₂, наибольшую гибкость λ_max=L/r_min и коэффициент φ₂, соот­ветствующий значению λ_max. Опреде­ляют напряжение в спроектированном сечении σ = N/(F·φ₂), ко­торое должно быть близким к [σ]_р. Допустимы отклонения σ от [σ]_р в пределах ±5%. В противном случае размеры поперечных сечений элементов изменяют в требуемом направлении. Обычно на второй или третьей итерации (повторении) подбора сечения результаты оказы­ваются удовлетворительными.

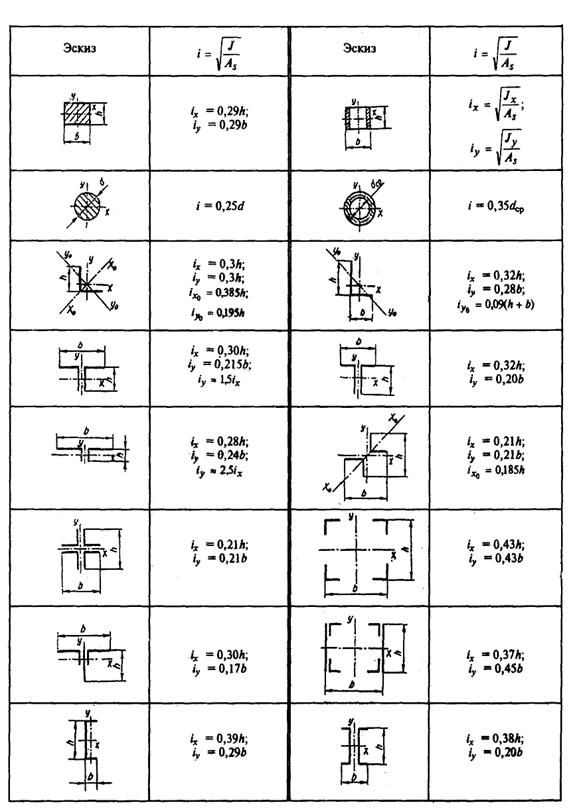
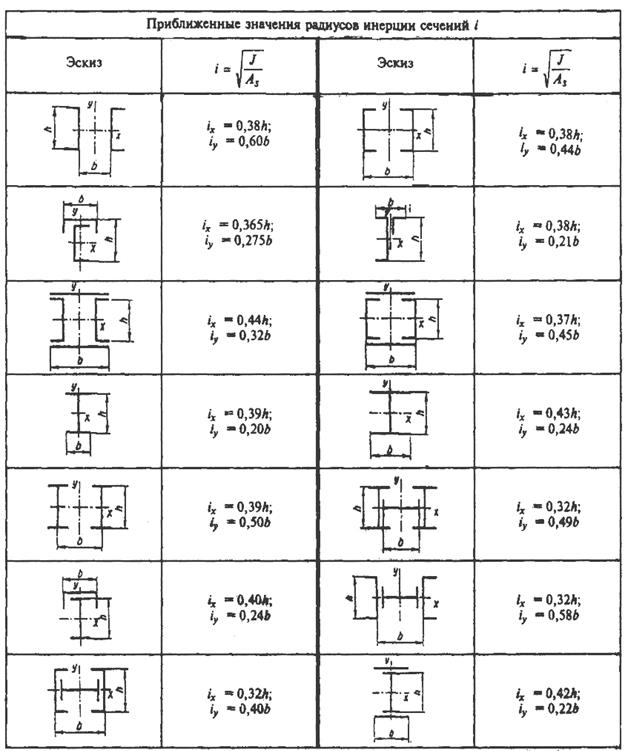
Приближенные значения радиусов инерции составных сечений стоек и колонн приведены в табл. 7.4

Гибкость как сжатых, так и растянутых элементов конструкций в методиках проектирования и СНиП различных конструкций обычно ограничивается предельной величиной, при превышении которой наблюдаются недопустимые в эксплуатации прогибы и деформации. Значения предельной гибкости элементов приведены в табл. 7.3

Таблица 7.3

Предельная гибкость λ_пр для элементов конструкций из стали и алюминия

Таблица 7.4

Приближенные значения радиусов инерции сечений i

Продолжение табл. 7.4

Пример расчета

Требуется подобрать поперечное сечение стой­ки; ее длина L = 8 м, продольная сжимающая сила Р = -940 кН; концы стойки закреплены шарнирно; материал - сталь класса С345 ([σ]р=240 МПа). Задаемся в первом приближении коэффициентом φ₁=0,6. Требуемая площадь поперечного сечения стойки по формуле (8.11) F_тр =0,940/(240·0,6)=0,00652 м² = 65,2 см².

Принимаем, что сечение сконструировано в форме сварного двутавра из двух листов 280х10 мм и одного 200x8 мм (вариант 1): F=72 см². Моменты инерции относительно осей х и y:

I_x=2(1³·28/12 +28·10,5²)+20³ ·0,8/12=6711 см⁴;

I_y =2·28³·1/12+0,8³·20/12= 3659 см⁴. Наименьший радиус инерции находим по формуле :

r_y= √3659/72= 7,13 cм;

гибкость по формуле (9.6): λ_y =800/7,13=112.

По табл.8.2 определяем, что при λ_y =112 для стали класса С345, φ=0,46 и подставляем в формулу (8.10):

σ = - 0,94/(0,46·72·10^-4)= -284 МПа.

Напряжение больше допустимого [σ]_p = 240 МПа. Увеличиваем размеры элементов стойки, чтобы возросла не только площадь, но и радиус инерции r_y. Для этого принимаем размеры листов полок 320x10 мм и стенки 250x8 мм (вариант 2).Тогда F=84 см².

Определяем момент инерции относительно оси у:

I_y=2·32³·1/12+25·0,8³/12=5462 см⁴.

Радиус инерции равен

r_y=√5462/82= 8,1 см.

Гибкость λ=800/8.1=100; φ=0,482. Затем находим напряжение сжатия:

σ=-0,940/(0,482·84·10^-4)=-232 МПа.

Стойка недогружена на 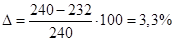. Сечение подобрано хорошо.