Устойчивость сжатых стержней
Если прямой стержень сжимать центрально приложенной силой Р, то вначале стержень будет оставаться прямым, и это состояние равновесия его будет устойчивым. Устойчивое состояние равновесия упругого стержня характеризуется тем, что при незначительном отклонении под влиянием какого-либо воздействия (малое возмущение) он возвращается в первоначальное состояние после прекращения этого воздействия, совершив незначительные затухающие колебания. Объяснить это можно так: внешняя сжимающая сила не может преодолеть сопротивление стержня тому незначительному изгибу, которому он подвергался при отклонении оси, а внутренняя упругая работа деформации изгиба стержня, полученная вследствие отклонения оси (потенциальная энергия изгиба ∆Е), больше внешней работы (∆А), которую совершила сжимающая сила в результате сближения концов стержня при его изгибе: ∆Е > ∆А (рис. 7.7 а). При дальнейшем увеличении сжимающая сила может достигнуть такого значения, что ее работа будет равна работе деформации изгиба, вызванного любым достаточно малым возмущающим фактором. В этом случае ∆Е = ∆А, и сжимающая сила достигает своего критического значения Ркр. Таким образом, прямой стержень при нагрузке его до критического состояния имеет прямолинейную форму устойчивого состояния равновесия.
При достижении силой критического значения его прямолинейная форма равновесия перестает быть устойчивой, стержень может изогнуться в плоскости наименьшей жесткости, и устойчивой формой равновесия у него уже будет криволинейная форма.
Если стержень имеет небольшую первоначальную кривизну (или незначительную внецентренность сжимающей силы), то при возрастании нагрузки он сразу же отклоняется от прямой. Это отклонение вначале мало, и только тогда, когда сжимающая сила приближается к критической (отличаясь от нее в пределах 1%), отклонения становятся значительными, что и означает переход в неустойчивое состояние.
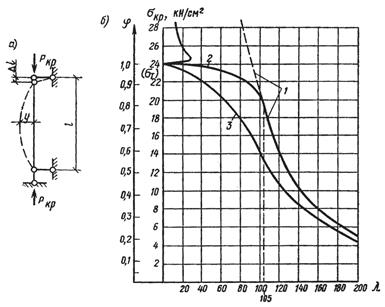
Рис. 7.7. Продольный изгиб центрально-сжатых стержней:
а - стержень с шарнирными соединениями; б - кривые критических напряжений и коэффициента продольного изгиба стали Ст3; 1- кривая Эйлера; 2 - кривая критических напряжений с учетом пластической работы материала; 3 - кривая коэффициента φ
Таким образом, неустойчивое состояние равновесия характеризуется тем, что уже при малом увеличении сил происходят большие перемещения. Дальнейшее незначительное увеличение сжимающей силы Р>Ркр вызывает всевозрастающие отклонения, и стержень теряет свою несущую способность. При этом различным видам закреплений стержня соответствуют различные значения критической силы. Для показанного на рис. 7.7 а центрально-сжатого стержня, имеющего по концам шарнирные закрепления (основной случай), критическая сила определена Л. Эйлером в виде
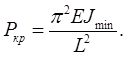 (7.1)
(7.1)
Напряжение, которое возникает в стержне от критической силы, называется критическим напряжением формула:
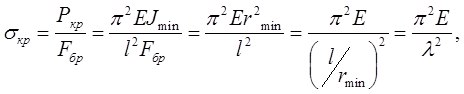 (7.2)
(7.2)
где 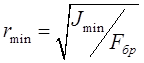 - минимальный радиус инерции;
- минимальный радиус инерции;
Fбр – площадь брутто поперечного сечения стержня;
λ = l/rmin – гибкость стержня, равная отношению длины стержня к радиусу инерции его сечения.
Из формулы (7.2) видно, что критическое напряжение зависит от гибкости стержня (так как числитель л2Е - величина постоянная), а гибкость - величина, зависящая лишь от геометрических размеров стержня. Следовательно, можно повысить критическое напряжение, изменяя гибкость стержня главным образом за счет увеличения радиуса инерции сечения. Эта возможность должна быть использована при конструировании. Таким образом, критическое напряжение можно также рассматривать как параметр, характеризующий выгодность подобранного сечения элемента, предназначенного для работы на сжатие. Графически формула Эйлера (7.2) изображается в виде гиперболы (рис. 7.7 б, кривая 1). Критические напряжения, определенные по формуле Эйлера, справедливы лишь при постоянном модуле упругости Е, т. е. в пределах пропорциональности, а именно для стержней большой гибкости (λ>105), что следует из уравнения (7.2) при σкр = σпц для стали Ст3 σпц =20 кН/см2, то λ = 105 (рис. 7.7).
Критические напряжения для стержней малой (λ < 30) и средней (30< λ <100) гибкости получаются больше предела пропорциональности, но меньше предела текучести. Теоретическое определение критических напряжений для таких стержней значительно усложняется, так как явление потери устойчивости происходит при частичном развитии пластических деформаций и переменном модуле упругости.
В результате многочисленных опытов, подтвердивших правильность теоретических выводов, для стержней малой и средней гибкости установлены критические напряжения, которые представлены в виде кривой на рис. 7.7 б (участок 2).
Для несущей способности сжатых стержней существенной является также местная устойчивость их элементов, которая зависит от гибкости полок, стенок или других элементов сечения стержня. Гибкость этих элементов определяется отношением характерных размеров их (ширины полок или высоты стенки сечения) к их толщине: b/δ или h/δ.
Итак, несущая способность самого элемента может быть исчерпана в результате того, что напряжение в конструкции достигло предела текучести (потеря прочности) или критического значения (потеря устойчивости). Эти две совершенно различные по своей природе причины нельзя смешивать.
Условия предельных состояний сжатых стержней по прочности и по устойчивости имеют вид.:
σ < σт /k; σ ≤ σ кр/ k,
где σ - напряжения в конструкции от расчетных нагрузок; k - коэффициент запаса.
Если обозначить отношение двух предельных напряжений коэффициентом φ
φ = σкр/ σт (откуда σкр = φ·σт),
то вторую проверку по устойчивости можно записать (учтя, что за наименьший предел текучести принимается расчетное сопротивление R)
σ = φ·σт /k = φ·R или для удобства расчета и сравнения результатов в виде рабочей формулы:
σ = N / (φ·Fбр ) ≤ R. (7.3)
Коэффициент φ, уменьшающий расчетное сопротивление до значений, обеспечивающих устойчивое равновесие, называется коэффициентом продольного изгиба. Нормами установлены значения коэффициента φ с учетом влияния случайных эксцентриситетов.
Коэффициент φ может интересовать нас только при значениях φ<1, так как в противном случае будет σкр> σт, т. е. возникает опасность потери несущей способности по прочности. Характеризуя критические напряжения, коэффициент φ является функцией гибкости стержня. На рис. 7.7 б приведена кривая 3 коэффициента φ. Значения коэффициента φ для сталей Ст3 и низколегированных приведены в табл.7.1.
Расчет на сжатие стержней из алюминиевых сплавов аналогичен расчету стальных стержней. Значения коэффициента φ для Al сплавов приведены в СНиП II-24-74.
Значения критических напряжений, а следовательно, и коэффициента φ в сильной степени зависят от способа закрепления концов стержней. Приведенные в табл.7.1 значения φ определены для основного случая продольного изгиба стержня, имеющего по концам шарниры. Для других способов закрепления стержней форма кривой продольного изгиба меняется, но ее можно привести к основному случаю путем замены действительной длины L расчетной (приведенной) длиной Lо, умножая длину стержня на коэффициент приведения μ. Тогда гибкость стержня при любом способе закрепления концов определится формулой
λ = L0 /r = μL /r , (7.4)
Таблица 7.1
Коэффициенты φ для стоек из малоуглеродистых
и низколегированных сталей
| Гибкость | Классы стали | ||||||
| элементов | С 235 | С 285 | С 345 | С 390 | С 440 | С 590 | С 750 |
| λ | Ст3 | Ст4 | низколегированные | ||||
| 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | |
| 0,988 | 0,987 | 0,986 | 0,985 | 0,984 | 0,983 | 0,982 | |
| 0,970 | 0,968 | 0,965 | 0,962 | 0,956 | 0,953 | 0,950 | |
| 0,943 | 0,935 | 0,932 | 0,927 | 0,916 | 0,909 | 0,903- | |
| 0,905 | 0,892 | 0,888 | 0,878 | 0,866 | 0,852 | 0,838 | |
| 0,867 | 0,843 | 0,837 | 0,823 | 0,810 | 0,790 | 0,760 | |
| 0,820 | 0,792 | 0,780 | 0,764 | 0,740 | 0,700 | 0,660 | |
| 0,770 | 0,730 | 0,710 | 0,682 | 0,650 | 0,610 | 0,558- | |
| 0,715 | 0.С60 | 0,637 | 0,604 | 0,570 | 0,518 | 0,432 | |
| 0,655 | 0,592 | 0,563 | 0,523 | 0,482 | 0,412 | 0,343 | |
| 0,582 | 0,515 | 0,482 | 0,437 | 0,396 | 0,336 | 0,288 | |
| 0,512 | 0,440 | 0,413 | 0,370 | 0,325 | 0,273 | 0,230 | |
| 0,448 | 0,383 | 0,350 | 0,315 | 0,275 | 0,230 | 0,192 | |
| 0,397 | 0,330 | 0,302 | 0,264 | 0,232 | 0,196 | 0,164 | |
| 0,348 | 0,289 | 0,256 | 0,228 | 0,198 | 0,168 | 0,142 | |
| 0,305 | 0,250 | 0,226 | 0,198 | 0,173 | 0,148 | 0,123 | |
| 0,270 | 0,220 | 0,200 | 0,176 | 0,153 | 0,130 | 0,100 | |
| 0,240 | 0,195 | 0,178 | 0,156 | 1,137 | 0,116 | 0,096 | |
| 0,216 | 0,175 | 0,160 | 0,139 | 0,122 | 0,102 | 0,086 | |
| 0,196 | 0,158 | 0,142 | 0,126 | 0,108 | 0,092 | 0,077 | |
| 0,175 | 0,142 | 0,129 | 0,112 | 0,098 | 0,082 | 0,069 | |
| 0,160 | 0,130 | 0,118 | 0,102 | 0,089 | 0,075 | 0,063 | |
| 0,146 | 0,119 | 0,108 | 0,093 | 0,081 | 0,068 | 0,057 |
Некоторые значения коэффициента приведения длины даны в табл.7.2.
Дата добавления: 2018-03-02; просмотров: 3785;
