Определение оптимального количества складов
в зоне обслуживания
В рамках настоящего курса проблема развития и размещения складов рассматривается в ключе концепции логистики, основным положением которой является реализация принципа системного подхода к управлению материальными потоками.
Складская сеть является значимым элементом логистических систем. Построение этой сети оказывает существенное влияние на издержки, возникающие в процессе доведения товаров до потребителей, а через них и на конечную стоимость реализуемого продукта.
Решения по развитию складской сети необходимо принимать на основеанализа полной стоимости, что означает учет всех экономических изменений, возникающих при изменении количества складов в логистической системе.
Рассмотрим модель системы распределения материального потока, представленную на рис.5. Допустим, что предприятие-поставщик, имеющее несколько складов, обслуживает сеть оптовых покупателей, расположенных на определенной территории. Количество покупателей и объемы потребляемых ими потоков в рамках данной задачи являются величинами постоянными.
На рисунке представлено три варианта организации распределения: с помощью одного, двух или шести складов (соответственно рисунки а, б и в). Очевидно, что в случае принятия варианта (а) транспортные расходы по доставке товаров со складов будут наибольшими. Вариант (в) предполагает наличие шести распределительных центров, максимально приближенных к местам сосредоточения потребителей материального потока. В этом случае транспортные расходы по товароснабжению будут минимальными. Однако появление в системе распределения пяти дополнительных складов увеличивает эксплуатационные расходы, затраты на доставку товаров на склады, затраты на управление всей распределительной системой. Не исключено, что дополнительные затраты в этом случае могут значительно превысить экономический выигрыш, полученный от сокращения пробега транспорта, доставляющего товары потребителям. Поэтому, возможно, что предпочтительнее окажется вариант (б), согласно которому район обслуживается двумя складами.

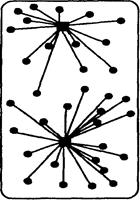
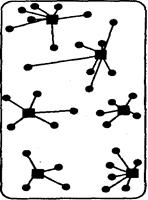
а) б) в)
Условные обозначения:
 - распределительные центры (склады);
- распределительные центры (склады);
 - потребители материального потока;
- потребители материального потока;
 - материальные потоки.
- материальные потоки.
Рис. 5. Варианты организации распределения материального потока:
а) с одним распределительным центром;
б) с двумя распределительными центрами;
в) с шестью распределительными центрами
Как видим, при изменении количества складов в системе распределения часть издержек, связанных с процессом доведения материального потока до потребителя, возрастает, а часть — снижается. Это позволяет ставить и решать задачу поиска оптимального количества складов. Рассмотрим графический метод решения данной задачи.
Выберем в качестве независимой переменной величину N — количество складов, через которые осуществляется снабжение потребителей. В качестве зависимых переменных будем рассматривать следующие виды издержек:
• транспортные расходы;
• расходы на содержание запасов;
• расходы, связанные с эксплуатацией складского хозяйства;
• расходы, связанные с управлением складской системой;
• потери продаж, вызванные удалением снабжающего склада от потребителя.
Для определения оптимального количества складов необходимо в разрезе всей системы распределения оценить, как в зависимости от изменения N изменяются те или иные расходы и потери.
Охарактеризуем зависимость издержек каждого вида от количества складов.
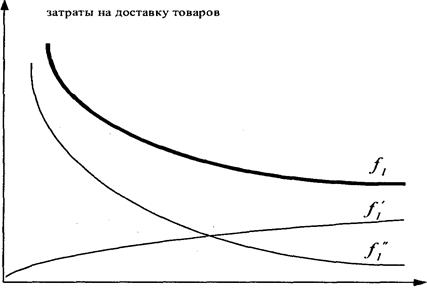
1. Зависимость величины затрат на транспортировку от количества складов в системе распределения (функция f 1, рис.6). В рамках решения данной задачи будем исходить из предположения, что для каждого значения переменной (количество складов) расположение складов на обслуживаемой территории оптимально, т. е. обеспечивает минимум затрат на транспортировку.
Весь объем транспортной работы по доставке товаров потребителям, соответственно и транспортных расходов, делят на две группы:
• расходы, связанные с доставкой товаров на склады системы распределения, т.е. расходы на так называемые дальние перевозки (функция f1’, рис. 6);
• расходы по доставке товаров со складов потребителям, т.е. расходы на так называемые ближние перевозки (функция f1’’, рис. 6).
Зависимость затрат на транспортировку от числа складов рассмотрим для каждой группы.
|
| общие затраты по доставке товаров затраты по доставке товаров на склады |
| затраты по доставке товаров потребителям |
| 1 2 3 4 5 6 7 8 N |
Рис. 6. Зависимость затрат на транспортировку от количества складов в системе распределения
При увеличении количества складов в системе распределения стоимость доставки товаров на склады возрастает, так как увеличивается количество поездок, а также совокупная величина пробега транспорта. Характер зависимости — не прямолинейный, так как здесь имеются условно-постоянная и условно-переменная составляющие, в результате чего расходы по доставке растут медленнее, чем расстояние.
Другая часть транспортных расходов — стоимость доставки товаров со складов потребителям с увеличением количества складов снижается. Это происходит в результате резкого сокращения пробега транспорта.
Суммарные транспортные расходы (функция f1, рис.6) при увеличении количества складов в системе распределения, как правило, убывают.
2. Зависимость затрат на содержание запасов от количества складов в системе распределения (функция f2 рис.7).
Увеличение количества складов в системе распределения влечет за собой сокращение зоны обслуживания отдельного склада, а, следовательно, и размера запаса на отдельном складе. Однако запас на отдельном складе сокращается не столь быстро, как зона обслуживания, в результате суммарный запас в распределительной системе возрастает.
Первая причина — необходимость содержания страхового запаса. В модели с несколькими складами страховой запас, в общем случае, необходимо создавать на каждом складе. Сокращение складской сети влечет за собой концентрацию страхового запаса и общее снижение потребности в нем. Ожидаемую экономию рассчитывают с помощьюзакона квадратного корня, согласно которому размер страхового запаса, а следовательно, и сумма издержек по его содержанию, возрастает пропорционально корню квадратному из числа складов.
Другая причина возрастания суммарного запаса заключается в том, что потребность складов в некоторых группах товаров при уменьшении зоны обслуживания может оказаться ниже минимальных норм, по которым товар получают сами склады. Это вынудит завозить данную группу на склады в количестве, превышающем потребность, что также повлечет за собой рост размера запаса. Можно привести и другие причины того, что при увеличении количества складов совокупный размер запаса в системе распределения увеличивается.
3. Зависимость затрат, связанных с эксплуатацией складского хозяйства, от количества складов в системе распределения (функция f3 рис.7).
При увеличении количества складов в системе распределения затраты, связанные с эксплуатацией одного склада, снижаются. Однако совокупные затраты распределительной системы на содержание всего складского хозяйства возрастают. Происходит это в связи с так называемым эффектом масштаба: при уменьшении площади склада эксплуатационные затраты, приходящиеся на один квадратный метр, увеличиваются. Например, в торговле при уменьшении площади склада с 10,5 тыс. м2 до 1,5 тыс. м2, т. е. в 7 раз, эксплуатационные затраты уменьшаются всего лишь в 5,25 раза. Замена одного склада семью (общая площадь остается той же — 10,5 тыс. м2), в этом случае, повлечет за собой увеличение эксплуатационных расходов в 1,4 раза.
Примерная зависимость величины удельных эксплуатационных расходов от размера склада (сфера торговли товарами народного потребления) приведена в табл. 2.
4. Зависимость затрат, связанных с управлением распределительной системой, от количества входящих в нее складов (функция f4, рис.7).
Характер данной зависимости представлен кривой f4. Здесь также действует эффект масштаба, в связи с чем при увеличении количества складов кривая расходов на системы управления делается более пологой.
Обязательным условием возможности эффективного функционирования распределительной системы, имеющей несколько складов, является компьютеризация управления. При отсутствии средств вычислительной техники кривая расходов на управление может принять совершенно иной вид, т. е. увеличение количества складов повлечет за собой резкое увеличение затрат на систему управления складским хозяйством. Следует отметить, что развитие распределительных складских систем в середине настоящего века сдерживалось именно отсутствием средств автоматизированной обработки информационных потоков.
Таблица 2
Примерная зависимость эксплуатационных затрат, в расчете на один квадратный метр площади склада, от размера складскойплощади
| Складская площадь, м2 | Эксплуатационные затраты, в расчете на 1 м2 склада, условных денежных единиц |
5.Зависимость потерь продаж, вызванных сокращением числа складов и соответствующим удалением снабжающего склада от потребителя, от количества складов в системе распределения (функция f5 рис.7).
При сокращении количества складов среднее расстояние до обслуживаемых пунктов возрастает. Это означает, что потребителю сложнее самому приехать на склад и выбрать ассортимент. Могут возникнуть задержки в пути следования груза. Действуют и другие негативные факторы, снижающие заинтересованность потребителя в более дальнем поставщике.
Зависимость падения оборота склада от расстояния до потребителя должна отслеживать служба маркетинга. Эта зависимость может носить различный характер. Например, в первом приближении, можно принять, что оборот падает на 1% с отдалением снабжающего склада от потребителя на 1 км.
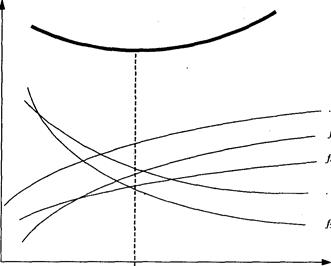
Зависимость совокупных затрат на функционирование системы распределения от количества входящих в нее складов (функция F) получают путем сложения всех приведенных на рис.7 графиков.Абсцисса минимума кривой совокупных затрат даст оптимальное значение количества складов в системе распределения (в нашем случае — 4 склада).
| затраты на функционирование системы распределения |
|
| F- совокупные затраты на функционирование системы распределения |
| f 2 затраты на хранение запасов f 3 затраты эксплуатационные f 4 затраты по управлению системой распределения f\ общие затраты по доставке товаров f 5 потери от удаления склада от потребителя |
1 2 3 4 5 6 7 8 N
N опт Количество складов
Рис.7. Зависимость совокупных затрат на функционирование системы
распределения от количества входящих в нее складов
Допустим, что упомянутое предприятие-поставщик имеет на территории обслуживания шесть складов. Переход к системе обслуживания с помощью четырех складов сопровождается увеличением одних издержек и сокращением других. Общий же размер издержек уменьшается (рис.8).
Полная стоимость распределения Полная стоимость распределения
при 6 складах при 4 складах
 |
Рис. 8. Общее снижение затрат, полученное в результате анализа полной стоимости распределения
В завершение следует отметить, что в последние годы в странах западной Европы наблюдается тенденция сокращения количества складов, особенно в розничной торговле. При этом, несмотря на рост транспортных расходов, в целом по системе распределения наблюдается экономия средств, особенно за счет сокращения страховых запасов.
Дата добавления: 2018-03-01; просмотров: 2031;
