Выбор критерия эффективности.

Математической моделью операции называются формальные соотношения, устанавливающие количественную связь принятого критерия эффективности, отражающего цель операции с действующими факторами. Очевидно, что чем удачнее будет подобрана математическая модель, чем лучше она будет отражать характерные черты явления, тем успешнее будет исследование и полезнее вытекающие из него рекомендации. Математические модели могут иметь вид формул, систем уравнений, неравенств, таблиц и т.п., отражающих количественную связь между критерием эффективности операции и параметрами, отражаемыми действующими в операции факторами.

На основе разработанной математической модели операции производится поиск решения – выбор определенных значений управляемых ОС факторов (стратегий) среди возможных, зависящих от нее. Решения, наилучшим образом отвечающие целям операции и предпочтительнее с точки зрения выбранного критерия эффективности называется оптимальными решениями.

При поиске решений, при исследовании операций необходимо различать два аспекта:

- подготовка решений (или рекомендации по выбору решений);

- принятие (выбор) окончательного решения.

Подготовкой решений занимается исследователь операций – специалист или группа специалистов (коллектив), осуществляющий: разработку стратегий, допустимых в операции; формализацию задачи; выбор критерия эффективности; разработку математической модели (или моделей) операции и отыскание среди множества возможных – оптимальных стратегий. Исследователь входит в состав оперирующей стороны.

Принятие решения – выходит за рамки исследования операций и относится к компетенции ответственного лица (или группы лиц), принимающего решение ЛПР, которому предоставляется право окончательного выбора и на которого возлагается ответственность за этот выбор.

Делая такой выбор, наряду с рекомендациями, вытекающими из математических расчетов, проведенных на разработанных математических моделях, они (ЛПР) могут учитывать ряд дополнительных соображений количественного и качественного характера, неучтенных в расчетах в виду несовершенства математического аппарата и из-за сложности их формализации (например, характер противника и т.п.).

Непременное участие лица, принимающего решения (ЛПР) даже в полностью автоматизированной системе управления, принимающей решение без непосредственного участия человека обеспечивается фактическим выбором одного из вариантов управляющего алгоритма, по которому осуществляется работа системы. Кроме того в АСУ обычно предусматривается возможность вмешательства человека в ход управляемого процесса.

Таким образом в качестве основных этапов исследования операций можно сформулировать следующие:

1. Выбрать критерий эффективности (один или несколько);

2. Определить совокупность активных средств, управляемых ОС и сформулировать стратегии – допустимые способы их использования;

3. Выявить основные факторы, действующие во время протекания операции;

4. Построить математическую модель операции;

5. В рамках принятой модели операции найти оптимальные (наилучшие) решения – отвечающие экстремальным значениям критерия эффективности среди всех возможных решений.

Выбор критерия эффективности.

Как уже говорилось, критерий эффективности операции – это показатель (или группа показателей), количественно отражающий цель операции, позволяющий сопоставлять между собой результаты предпринимаемых действий и цель операции.

Они должны отвечать следующим основным требованиям:

- представительность;

- критичность к исследуемым параметрам;

- максимально возможная простота;

- объединение в себе по возможности всех основных элементов исследуемой операции;

- правильный учет стохастических факторов.

Рассмотрим их подробнее.

1. Представительность. Критерий должен позволять оценивать эффективность основной задачи операции, а не второстепенных. Неправильный выбор критерия приводит к тому, что все исследования, проведенные на его основе оказываются бесполезными, а полученные решения – нецелесообразными, а подчас вредными, и приводящими к неоправданным затратам и потерям (например, пресловутый “Вал” в качестве основного критерия оценки хозяйственной деятельности предприятий).

2. Критерий должен быть критичным, т.е. чувствительным к изменениям исследуемых параметров. Чем эта критичность выше, тем лучше.

3. Критерий должен быть простым, т.к. введение в него второстепенных составляющих может усложнить исследования, не приводя к уточнениям получаемых выводов, не позволяя выявить основных результатов (эффектов) операции, как говориться “за деревьями не видно леса”.

4. Желательно, чтобы критерий был единым, т.к. решение задачи исследования и поиска “наилучших” решений при наличии двух и более критериев крайне затруднено и без введения дополнительных предположений, условий не дает возможности использования строгих математических методов. Однако следует отметить, что сведение задачи к одному критерию не всегда позволяет в полной мере учесть все цели, стоящие перед операцией, что значительно обедняет задачу и не всегда возможно. В этом случае приходим к необходимости формирования векторного критерия эффективности.Проблемы поиска решений в этом случае представляют собой особую задачу и будут рассматриваться отдельно.

5. При учете стохастического характераисследуемых процессов при выборе критерия эффективности необходимо учитывать возможность повторяемости операции, осреднения ее результатов по многим реализациям, характер неопределенности случайных факторов и т. п.

Ограничимся, для начала, рассмотрением задач исследования операций с одним (скалярным) критерием эффективности.

Обозначим:

- а совокупность действующих в операции факторов, неуправляемых ни одной из сторон, значения которых известны заранее и детерминированы и в ходе операции не изменяются.

- xÎX – совокупность факторов, управляемых оперирующей стороной, характеризующих ее поведение во время операции и составляющих в совокупности решение (X – множество всех возможных решений ОС) (стратегии ОС).

- yÎY – совокупность факторов, управляемых противодействующей стороной (Y – множество всех возможных решений ПС) (стратегии ПС).

- zÎZ – множество факторов, не контролируемых ни оперирующей, ни противодействующей стороной, значения которых заранее не известны. (Z – множество их всех возможных значений).

Тогда значение, которое примет показатель эффективности W в результате операции зависит от всех этих групп факторов и может быть записано как некий функционал

W = W(a, x, y, z)

В зависимости от вида цели, стоящей перед операцией можно различить два вида критериев эффективности: “качественные” и “количественные”.

В первом случае (качественный критерий эффективности) целью операции является достижение определенного заданного результата (эффекта), который может быть получен или не получен, и, соответственно, поставленная цель является выполненной, если этот результат достигнут и не выполненной – в противном случае. Например, изготовление работоспособного изделия, успешная (безаварийная) посадка ЛА, поражение цели и т.д.

В этом случае результат операции может быть оценен двумя числами:

1 – если цель операции достигнута;

0 – если цель операции не достигнута.

Если все факторы, влияющие на операцию детерминированы, то

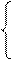0 – если результат достигнут;

W = W(a, x*, y*,) =

1 – если результат не достигнут.

Здесь x*, y* - фиксированные значения управляемых факторов.

Если же на ход операции оказывают влияние случайные факторы Z, то значение показателя W = W(a, x*, y*, z*) также будет случайно и использование его в качестве критерия эффективности в этом случае невозможно.

Во втором случае (количественный критерий эффективности) целью операции является получение наилучшего значения некоторой величины, оценивающей конечный эффект операции.

Например, объем выпускаемой продукции, время безотказной работы оборудования, число пораженных самолетов противника и т.д.

Если при этом все факторы, влияющие на результат операции, детерминированы, то в качестве критерия эффективности можно использовать значение этой величины

W = W(a, x*, y*).

При наличии случайных, статистически определенных факторов, влияющих на результат операции в качестве критерия эффективности можно, например, принять математическое ожидание некоторой случайной величины R, характеризующей результат операции

W = Mz[R(a, x*, y*, z)] = W(a, x*, y*),

или каких-либо других величин, полученных с учетом случайности R.

При известном законе распределения f(z) случайных факторов Z значение W может быть найдено как

W(a, x*, y*) = ò R(a, x*, y*, z)*f(z)dz

ZÎZ

где f(z) – плотность распределения вероятностей случайных факторов Z.

Как видно, неопределенность значений вершины R, связанная с неизвестными заранее значениями, которые примет в ходе операции случайная величина Z при этом устраняется.

Следует заметить, что применение в качестве критерия эффективности математического ожидания возможно только тогда, когда допустимо осреднение результатов операции либо при многократном ее повторении ( например, среднее время безотказной работы оборудования при многократной его эксплуатации), либо, если осреднение результатов может быть осуществлено в ходе одной операции за счет большого числа одновременно выполняемых однотипных действий (например, число “хороших” изделий, выпускаемых цехом на 100 станках автоматах в течение смены), т.е. “недостача” показателя в одном случае может быть компенсирована “избытком” в другом (например, суммарный доход в случае многократного повторения операции.

Если же осреднение результатов по многим операциям недопустимо или большой разброс относительно среднего, то использование в качестве критерия эффективности математического ожидания может привести при приемлемых средних показателях к недопустимым результатам в одной отдельной операции (например, среднее число успешных полетов в авиации).

В этих случаях в качестве показателя эффективности можно использовать вероятность, что случайная величина R, характеризующая результат операции достигнет значения, не менее заданного

W = Pz[R(a, x*, y*, z)³Rзад]

или иначе

W = ò f(z)dz = W(a, x*, y*).