Представление чисел в двоично-десятичном коде
При двоично-десятичном представлении чисел, каждый разряд числа представляется в двоичной форме. Для представления каждой десятичной цифры необходимы четыре двоичных разряда; эти четыре разряда на практике называют тетрадой, при этом из всех возможных комбинаций двоичного представления тетрады выбираются только десять — по числу цифр в десятичной системе счисления. Существует несколько способов кодирования десятичных цифр: на выбор формы представления оказывает влияние необходимость выполнения арифметических операций либо каких-либо других операций с числами. Для выполнения этих требований сформулированы пять основных положений, предъявляемых системе кодирования:
1. Единственность, то есть между каждой десятичной цифрой и ее двоичным эквивалентом должно быть установлено взаимнооднозначное соответствие, что обеспечивает эффективность процесса кодирования (декодирования);
2. Упорядоченность. Если разряды тетрады имеют веса в двоичной системе счисления, то большая десятичная цифра должна изображаться большей тетрадой, что обеспечивает эффективность сравнения в двоично-десятичном преобразовании;
3. Четность. Всем четным или нечетным десятичным цифрам должно соответствовать либо только четное, либо только нечетное представление числа в двоичном коде. Только в этом случае будет обеспечена эффективность операций округления, умножения и деления;
4. Дополнительность. сумма двоичного кода десятичной цифры и ее обратного двоичного кода должна быть равна коду цифры "9", что обеспечивает эффективность переноса в старший разряд, а также формирования прямого и дополнительного кодов. двоично-десятичный эквивалент суммы двух десятичных цифр при выполнении этого требования может быть получен как сумма двоично-десятичных кодов слагаемых, что упрощает проведение операций арифметического суммирования;
5. Взвешенность. Каждому из разрядов двоичного представления десятичной цифры можно поставить в соответствие показатель степени основания системы счисления строго в упорядоченном порядке, что обеспечивает эффективность всех арифметических и логических операций.
Таблица представления десятичных цифр с использованием различных кодов.
| цифра | СИСТЕМЫ КОДИРОВАНИЯ | |||||
| 8421+3 | код Грея | |||||
| отсутсвует дополнительность | единственная, котрая удовлетворяет дополнительности | отсутствуют четность, дополнительность, взвешенность; имеет локоничное представление (не более двух"1") | отсутствуют единственность, дополнительность, взвешенность; нет ни одного состояния >9; нет лишних состояний | отсутствуют единственность;создана для упрощения операции умножения | относится к циклическим кодам, которые характеризуются тем, что последующая комбинация двоичных чисел отличается от предыдущей только в одном разряде |
Пример: формирование чисел в коде Грея
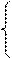 ai Å ai+1 i < n
ai Å ai+1 i < n
ai =
ai+1 i = n
| КОДЫ | |
| двоичный | Грея |
Ниже представлена схема логического устройства, выполняющего операцию преобразования двоичного кода в код Грея.
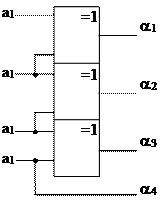 |
Рис. 1.21Логическое устройство, выполняющее операцию преобразования двоичного кода в код Грея
Выполнение арифметических операций при двоично-десятичном кодировании
Пример: 1703 + 300 = 2003
0001 0111 0000 0011
0011 0000 0000
0001 1010 0000 0011
0110 .
0010 0000 0000 0011
При сложении чисел в двоично-десятичном коде, с весами разрядов 8421 необходимо корректировать состояния тех тетрад, где получилось 10 и более, начиная с младшей, добавлением числа "6" (в двоичном коде: 0110).
Пример: 1812 – 1421 = 391
0 0001 1000 0001 0010
1 0001 0100 0010 0001 — обратный код
1010 1101 1010
0110 0110 0110
 10 0000 0011 1001 0001
10 0000 0011 1001 0001
Для представления отрицательного числа в обратном двоично-десятичном коде в знаковый разряд записывается "1", а в остальные разряды числа — дополнение до десятичного числа 10 n - 1, где n — число разрядов исходного десятичного числа; для представления отрицательного числа в дополнительном двоично-десятичном коде в знаковый разряд записывается "1", а в остальные разряды числа дополнения до числа 10 n, где n — число разрядов исходного десятичного числа.
Дата добавления: 2018-03-01; просмотров: 2504;
