Уравнение Бернулли. Дифференциальные уравнения движения идеальной жидкости

В движущейся идеальной жидкости, плотность которой 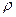, выделим элементарный параллелепипед размерами 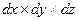и запишем дифференциальные уравнения движения этого объема жидкости в координатной форме, рассматривая его как материальную точку.

На элемент действуют составляющие сил давления и массовых сил, интенсивность которых на единицу массы по направлению осей равна 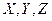(рис. 6.1).

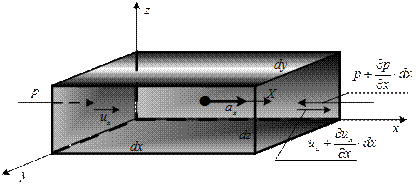Рис. 6.1

На рисунке показаны только составляющая массовых сил по оси 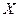, давление на гранях перпендикулярных оси 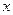и составляющая ускорения по оси 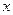, что позволяет записать уравнение движения выделенного объема в направлении оси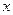

.

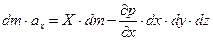(6.1)

Так как масса элементарного объема легко определяется через массовую плотность

,

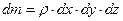(6.2)

то после деления обеих частей уравнения (6.1) на (6.2), получаем

.

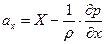(6.3)

С учетом того, что 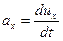, где 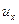– проекция скорости элементарного объема на ось 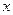, уравнение (6.3) принимает вид

.

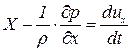(6.4)

Действуя аналогично можно получить уравнения движения выделенного элемента в направлении осе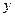й и 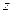. Таким образом система дифференциальных уравнений движения идеальной жидкости в декартовой прямоугольной системе координат имеет вид

, ,

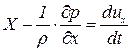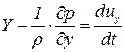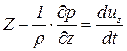
(6.5)

Уравнение Бернулли для установившегося движения при действии

потенциальных сил

Последовательно умножим уравнения (6.5) на и сложим полученные результаты

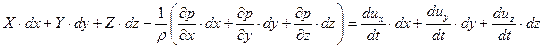
(6.6)

При установившемся движении

,

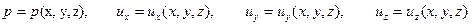(6.7)

тогда в рассматриваемый момент времени

.

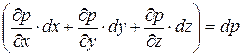(6.8)

В движущейся жидкости размеры элементарного параллелепипеда 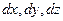можно определить через составляющие скорости частицы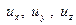

.

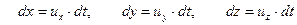(6.9)

С учетом (6.9) правая часть уравнения (6.6) приводится к виду

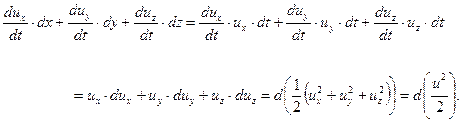
(6.10)

Если движение жидкости происходит в потенциальном силовом поле, то составляющие интенсивности массовых сил определяются через потенциальную энергию этого поля, приведенную к единице массы

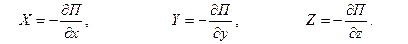
(6.11)

Принимая во внимание (6.11), первое слагаемое в левой части уравнения (6.6) можно записать так

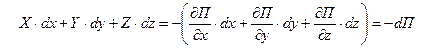
(6.12)

С учетом (6.8), (6.10), (6.12) уравнение (6.6) принимает следующий вид

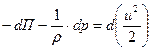
(6.13)

Так как идеальная жидкость – это несжимаемая жидкость, и 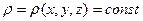(6.13) можно записать в виде

,

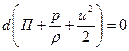(6.14)

или

.

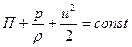(6.15)

Уравнение (6.15) и является уравнением Бернулли для элементарной струйки идеальной жидкости при установившемся движении, когда элементарную струйку можно отождествлять с линией тока. Для различных линий тока значения константы в уравнении (6.15) будут разными.

Замечание. Более детальное изучение движения частицы жидкости позволяет установить, что при изменении положения в пространстве происходит изменение ее формы и объема. Движение можно представить как сумму трех движений: поступательного (вместе с полюсом), деформационного (за счет изменения размеров) и вращательного (вокруг мгновенной оси, проходящей через полюс).

По характеру движения частиц различаютвихревое и потенциальное движения.

Вихревым движением называют такое движение, при котором движущиеся частицы жидкости вращаются вокруг осей, проходящих через их полюсы. Вихревое движение характеризуется вихревыми линиями – линиями, в каждой точке которых касательная совпадает с вектором угловой скорости .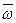

Движение, при котором такое вращение отсутствует, называется безвихревым или потенциальным движением.

Уравнение Бернулли справедливо:

· вдоль линии тока;

· на вихревых линиях;

· при винтовом движении, когда векторы линейной и угловой скоростей параллельны (линия тока совпадает с вихревой линией);

· при потенциальном движении;

· при статическом равновесии жидкости.

Проведем детальное рассмотрение параметров, характеризующих движение жидкой частицы, но ограничимся только движением в плоскости xy (рис. 6.2).

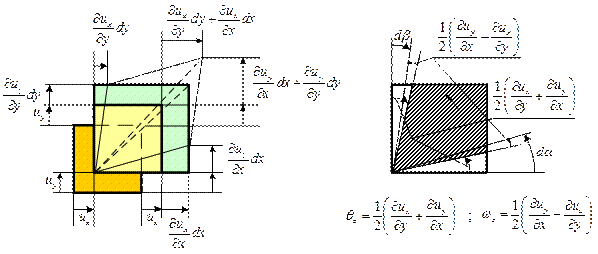Рис. 6.2

Частица жидкости в форме прямоугольного параллелепипеда (рис. 6.1) имеет в точке О локальную скорость, составляющие которой равны 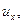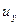, 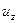. Если О полюс, движущейся частицы, за время 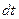сместится на расстояние 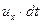в направлении оси x и на расстояние 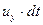в направлении оси y, то за счет приращения скорости в направлении осе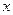й и 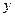ребра частицы получат абсолютные удлинения:

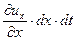- по о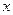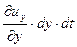си ; - по оси .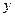

(6.16)

Кроме деформаций удлинения частица в окрестности точки О претерпевает деформации сдвига, характеризуемые углам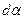и и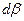

; .

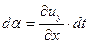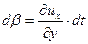(6.17)

Суммарную деформацию сдвига в плоскости 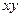равную 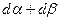можно разложить на две составляющие:

деформацию сдвига, характеризуемую углами

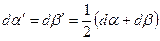
(6.18)

и поворот частицы относительно оси 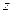, проходящей через полюс О, на угол

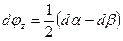
(6.19)

Следовательно, изменение положения и формы частицы в плоскости 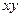характеризуется:

скоростями линейных относительных деформаций

,

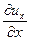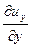
(6.20)

скоростью деформации сдвига

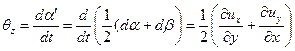
(6.21)

угловой скоростью вращения частицы относительно оси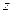

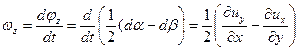
(6.22)

В общем случае деформационное движение частицы характеризуется:

скоростями линейных деформаций

, , ;

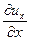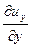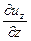(6.23)

скоростями угловых деформаций

;

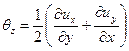
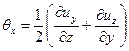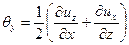
(6.24)

составляющими мгновенных угловых скоростей

;

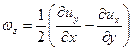
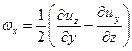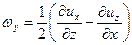
(6.25)

Вектор мгновенной угловой скорости 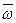направлен по нормали к плоскости в которой происходит вращение, а его модуль легко определяется по составляющим

.

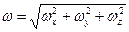(6.26)

С направлением вектора 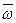связано определение вихревой линии – линии, в каждой точке которой вектор угловой скорости совпадает с направлением касательной к этой линии (рис.6.3).

Рис. 6.3

Дифференциальное уравнение вихревой линии имеет вид

,

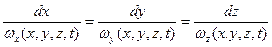(6.27)

где 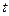рассматривается как параметр.