Основные формулы исчисления индивидуальных и сводных индексов

Наименование индекса	Формулы расчета индексов
Индивидуальный индекс	Агрегатный индекс	Средний индекс
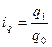
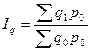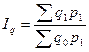
Индекс физического объема продукции (по цене)		1) с весами базисного периода: 2) с весами текущего периода:	1) средний арифметический: 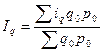2) средний гармонический:
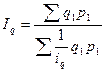
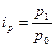
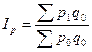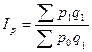
Индекс цен		1) с весами базисного периода (по Ласпейресу): 2) с весами отчетного периода (по Пааше):	1) средний арифметический: 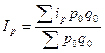2) средний гармонический:
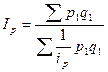
Индекс стоимости продукции (товарооборота)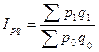
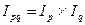
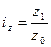
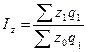
Индекс себестоимости продукции			1) средний арифметический: 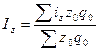2) средний гармонический:
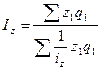
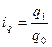
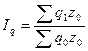
Индекс физического объема продукции (по себестоимости)			1) средний арифметический: 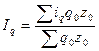2) средний гармонический:
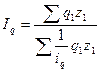
Индекс издержек производства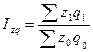
Индекс производительности труда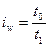
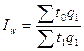
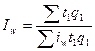
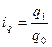
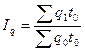
Индекс физического объема продукции (по трудоемкости)			1) средний арифметический: 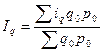2) средний гармонический:
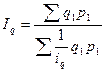
Индекс затрат времени на производство продукции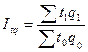

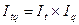
Общие индексы показывают, на сколько процентов изменился размер индексируемой величины в отчетном периоде по сравнению с базисным. Для того чтобы рассчитать абсолютное изменение индексируемой величины, необходимо определить разность числителя и знаменателя соответствующего индекса.

Например, разность числителя и знаменателя индекса товарооборота показывает, на сколько денежных единиц увеличилась (уменьшилась) стоимость продукции в текущем периоде по сравнению с базисным одновременно за счет изменения объема продаж и цен.

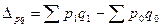
Разность числителя и знаменателя индекса цен показывает экономию (перерасход) покупателей в абсолютном выражении в текущем периоде по сравнению с базисным за счет изменения цен.

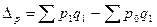
Разность числителя и знаменателя индекса физического объема продукции показывает, как в абсолютном выражении изменилась стоимость продукции за счет изменения объема ее производства:

.

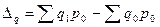Индексы цен

Особое место среди индексов качественных показателей отводится индексам цен. Основным назначением индекса цен является оценка динамики цен на товары производственного и непроизводственного потребления.

В практике статистики используются два основных вида формул индекса цен: формула Ласпейреса и формула Пааше (табл. 7.1). Значения индексов неодинаковые, т.к. они имеют разное экономическое содержание. Индекс цен, исчисленный по формуле Пааше, показывает, насколько товары в отчетном периоде стали дороже (дешевле), чем в базисном. Индекс цен Ласпейреса показывает, во сколько бы раз товары базисного периода подорожали (подешевели) из-за изменения цен на них в отчетном периоде. При этом индекс Пааше преобразуется в средний гармонический индекс цен, а индекс Ласпейреса - в средний арифметический индекс.

Согласно практике, индекс цен Пааше имеет тенденцию некоторого занижения, а индекс цен Ласпейреса - тенденцию некоторого завышения. Таким образом, индекс Пааше численно должен быть меньше индекса Ласпейреса. Разница в результатах расчета по этим формулам называется эффектом Геншенкрона.

Для определения более реального изменения цен в статистике используется формула идеального индекса цен Фишера, который представляет собой среднюю геометрическую из индексов Пааше и Ласпейреса:

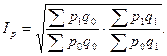
Геометрическая форма индекса лишена конкретного экономического содержания. В отличие от индексов Ласпейреса или Пааше разность между числителем и знаменателем этого индекса не покажет никакой реальной экономии (потерь) из-за изменения цен.

Идеальность формулы Фишера состоит в том, что при перестановке базисного и отчетного периодов полученный индекс является обратной величиной для первоначального индекса.

В силу сложности экономической интерпретации индекс Фишера на практике используется крайне редко. Чаще всего он применяется при исчислении индексов цен за длительный период времени, для сглаживания тенденций в структуре и составе объема продукции, в которых происходят значительные изменения.

Формулы Ласпейреса и Пааше являются расчетными для исчисления индекса инфляции, индекса потребительских цен и индекса-дефлятора (глава 19).

При сравнении цен двух стран или регионов (А и В) в статистике рассчитывают территориальные индексы цен:

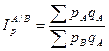или .

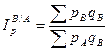Эти формулы дают совершенно различное представление о соотношении уровней явления и естественно имеют разные результаты. В теории и практике статистики для решения этой проблемы применяется метод стандартных весов, который заключается в том, что значения индексируемой величины взвешиваются не по весам какого-либо одного региона, а по весам двух регионов вместе либо области, в которой эти регионы находятся. Для этого стоят индекс цен со стандартными весами Эджворта:

.

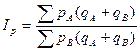Кроме перечисленных индексов цен, в статистике финансов используются следующие индексы (глава 23):

1. Индекс Доу-Джонса (Dow Jones Industrial Average Index) - средний арифметический индекс значений курсов акций, котирующихся на Нью-Йоркской фондовой бирже. Один сводный и три групповых индекса рассчитываются каждые полчаса, а их значение ежедневно публикуется на момент закрытия биржи.

2. Индекс Стэндарда и Пура (Standard and Poor’s 500 Stock Index) - индекс, рассчитываемый по курсам акций 500 крупнейших компаний Нью-Йоркской фондовой биржи, как средневзвешенный показатель, учитывающий общее количество выпущенных акций.