Теоретические сведения

Рассмотрим активный элемент (транзистор, электронная лампа), 3 зажима которого соединены комплексными проводимостями 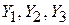, как показано на рис. 6.1. Считаем, что в эти проводимости входят также входные 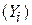, выходные 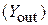и проходные 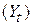проводимости активного элемента, за исключением переходной проводимости (крутизны характеристики 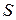), а также проводимости нагрузки 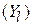. В дальнейшем проводимости активного элемента не учитываются и полагаются равными нулю. Кроме проводимостей активного элемента в проводимости 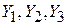входят внешние (навесные) проводимости 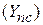. Тогда выражения для проводимостей будут иметь следующий вид:

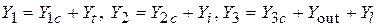. Суммарная проводимость их соединения 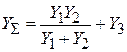. На резонансной частоте 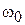мнимая часть 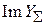должна обращаться в ноль. Будем полагать, что активный элемент включен как усилитель напряжения (схемы с заземленным эмиттером, заземленным истоком, заземленным катодом). Тогда напряжение на его входе 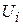(на проводимости 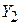) будет меньше выходного напряжения 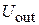(на проводимости 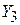). Соотношение между этими напряжениями определяется коэффициентом передачи цепи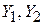 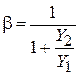, где ‒ коэффициент обратной связи. Так как фаза выходного напряжения усилителя повернута на 180˚ по отношению к входному, для получения положительной обратной связи фазосдвигающая цепь 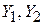должна обеспечить такой же поворот фазы. Следовательно, коэффициент должен быть вещественным и отрицательным, для чего 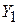и 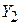должны иметь разные знаки и модуль отношения 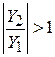. 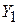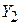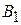Это возможно лишь при условии, что мнимые компоненты и ( и 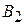) имеют разные знаки и 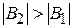. Фазосдвигающая цепь резонирует на частоте, отличной от 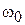. Для резонанса на частоте 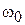контур дополняется проводимостью 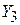, мнимая часть которой 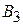имеет тот же знак, что и 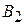, и значение 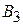обеспечивает выполнение равенства 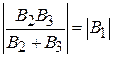. На частоте резонанса 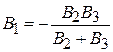и тогда .

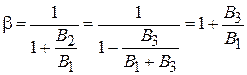Такая конфигурация схемы, когда активный элемент присоединен внешними выводами к трем определенным точкам колебательного контура, носит название «трехточечной». В диапазоне СВЧ чаще всего используется вариант «емкостной трехточки» (в зарубежной литературе – «схема Колпица»), когда 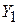реализуется в виде индуктивности, а 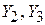‒ в виде емкостей.

Качество работы АГ в очень большой степени зависит от добротности его колебательной системы. Если рассматривать колебательный контур, образованный только навесными элементами 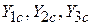, то его «собственная» добротность 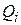определяется главным образом добротностью индуктивного звена, так как добротность емкостей заметно выше, чем добротность индуктивностей. В схеме с активным элементом добротность уменьшается благодаря активным компонентам проводимостей 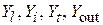. Такая добротность называется «нагруженной» добротностью 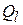. По определению добротность равна отношению энергии, запасаемой в реактивном элементе контура на частоте резонанса (энергия, запасаемая в индуктивности или емкости, одинакова), к энергии, расходуемой на потери во всех элементах контура: 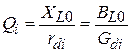. Здесь в числителях, соответственно, реактивные сопротивление и проводимость индуктивности на частоте резонанса, в знаменателях, соответственно, активные сопротивления и проводимости потерь в контуре без активного элемента, пересчитанные к индуктивности. Выражение для нагруженной добротности отличается тем, что в сопротивление и проводимость потерь включены потери, связанные с активным элементом и нагрузкой. Определим активные составляющие проводимостей 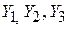: 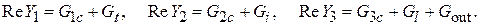Ниже приведено выражение для проводимости потерь 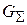, пересчитанной параллельно 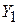в предположении, что 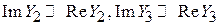. Эти условия всегда выполняются для высокодобротных контуров. Тогда 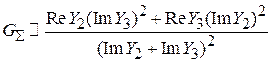и нагруженная добротность будет 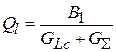. Здесь 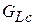‒ собственная проводимость потерь индуктивности. Перейдем к анализу работы АГ в линейном приближении.

ВАХ транзисторов (биполярных и полевых), а также таких электронных ламп, как пентоды и тетроды, таковы (малая зависимость выходного тока от напряжения питания), что их можно рассматривать как источники тока. Тогда ток, протекающий через колебательный контур, будет равен: 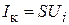, где 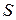‒ крутизна характеристики активного элемента в области рабочих токов АГ, 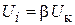‒ напряжение на входе активного элемента, а 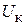‒ напряжение на контуре (на проводимости 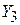). Колебательный контур (КК) АГ состоит из двух параллельно включенных цепей – цепи 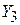и цепи последовательно включенных 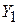и 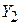. Для емкостной трехточки 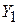есть индуктивность, а 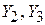‒ емкости. Проводимость цепочки 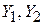равна 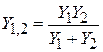. В предположении высокой добротности КК приближенное значение этой про водимости: 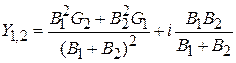. Так как ранее все активные проводимости были перечислены к 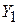, то 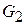можно положить равным нулю и тогда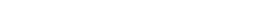 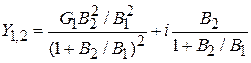. Ранее было показано, что величина коэффициента обратной связи определяется как:

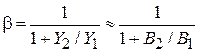. Тогда 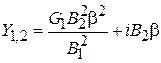. Из выражения для следует, что 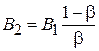, тогда 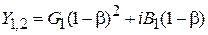. Активная проводимость 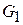включает в себя все потери КК, и поэтому 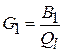. Следовательно, окончательно 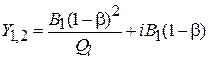. Поскольку для обеспечения положительной обратной связи значение должно быть вещественным и отрицательным, 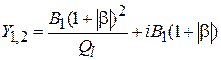. Тогда КК может быть представлен в виде параллельного соединения трех проводимостей: активной 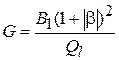, индуктивной 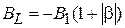и емкостной 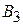. Теперь удобно перейти от проводимостей к сопротивлениям: активное сопротивление 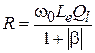, индуктивно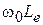е , где 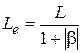, и емкостное 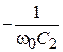(рис. 6.2). Все эти сопротивления соединены параллельно, и через них текут ток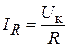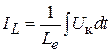и: , и 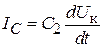. Сумма этих токов должна быть равна току 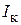, который создается активным элементом: 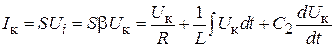. Принимая во внимание, что напряжение 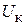на КК АГ (благодаря его высокой добротности) содержит практически только первую гармонику сигнала, создаваемую первой гармоникой тока 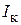, вместо статической крутизны 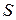надо использовать крутизну по первой гармонике 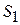. Тогда уравнение примет вид: 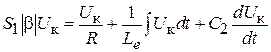. Продифференцировав это уравнение по времени, получаем дифференциальное уравнение следующего вида: 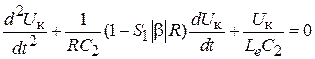. Решением этого уравнения будет: 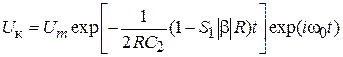, где 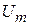‒ амплитуда колебаний, 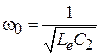. Самовозбуждение АГ возможно лишь, если 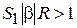. Заметим, что самовозбуждение начинается с малых амплитуд, при отсутствии отсечки коллекторного тока, и поэтому крутизна 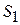в начале процесса самовозбуждения равна крутизне в рабочей точке 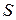. Подставив в это выражение представление 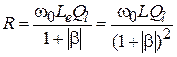получим условие 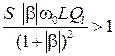. Крутизна 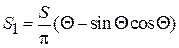, где 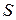‒ статическая крутизна активного элемента в выбранной рабочей точке, а 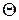‒ угол отсечки. В начале процесса самовозбуждения, пока напряжение 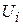мало, угол отсечки можно считать равным 180º и 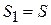. При достижении установившегося состояния угол отсечки равен 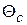и должно выполняться условие 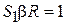, откуда 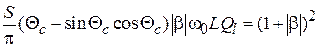. Задавшись значениями 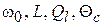( 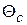выбирают в пределах 45º… 90º) определяют значение . Индуктивность 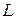выбирают так, чтобы произведение 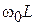было порядка 100 Ом. Нагруженную добротность 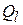желательно иметь порядка половины собственной добротности 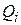КК АГ [1]. Большое значение 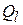требует слабой связи транзистора с КК, т. е. малого значения , а это в свою очередь требует, чтобы 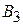было значительно меньше 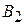( 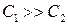). Крутизна 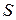существенно зависит от частоты (так как элемент матрицы рассеяния транзистора 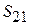уменьшается с увеличением частоты).

6.1.2. Об использовании отрезков линий передачи

в качестве индуктивностей в ГУН.

Отрезок ЛП, закороченной на конце, длиною менее 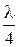имеет входное сопротивление вида 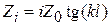, где 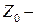волновое сопротивление ЛП; 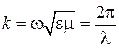( 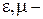параметры среды, заполняющей ЛП, 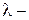длина волны в ЛП); 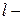геометрическая длина ЛП. Если не учитывать потери в ЛП, то 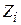является чисто мнимым и имеет индуктивный характер. При 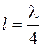тангенс обращается в бесконечность. Следовательно, можно использовать равенство 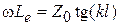, где 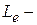эквивалентная индуктивность ЛП. Тогда 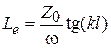. В отличие от обычной сосредоточенной индуктивности 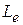зависит от частоты. Если угол 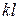меньше 30°, то тангенс можно заменить его аргументом. Тогда 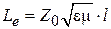и для коротких отрезков ЛП можно считать, что 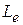не зависит от частоты. Однако для получения больших значений 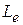приходится увеличивать 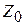, что приводит к росту потерь и снижению добротности. При использовании отрезков ЛП с углом, большим 45˚, величина 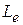становится существенно зависимой от частоты, так как с ростом частоты функция 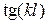растет быстрее, чем частота, и, следовательно, значение 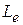растет с увеличением частоты. Для АГ, работающих на фиксированной частоте, это не имеет значения, однако является существенным для ГУН. Действительно, если выбрать 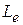на нижней частоте, при максимальной емкости варикапа, то при уменьшении емкости варикапа и росте частоты, генерируемой ГУН, в свою очередь будет расти 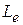, что приведет к уменьшению частоты по сравнению с ГУН, в котором используется сосредоточенная индуктивность.Оценим приближенно изменения частоты в ГУН с сосредоточенной индуктивностью и в ГУН с резонатором. В ГУН СВЧ полная емкость КК АГ зависит от управляющего напряжения 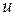, т. е. 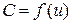. Резонансная частота КК с сосредоточенной индуктивностью определится как 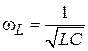, где 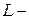индуктивность КК. Преобразуем это выражение так, чтобы в него входило сопротивление индуктивности 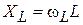, тогда получим: 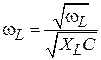, или 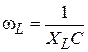. Следовательно, для ГУН с коаксиальным резонатором (КР) 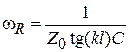. Оценим теперь изменение резонансной частоты для обоих КК при изменении емкости 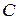. Очевидно, что для 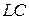КК справедливо отношение 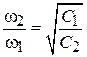. Для резонаторного КК функция 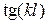зависит от частоты и для резонансных частот 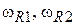будут справедливы уравнения вида: 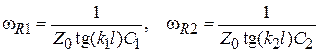. Поделив одно на другое, получаем равенство 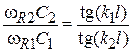, в котором неизвестным является только длина КР 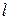. Для определения длины получаем трансцендентное уравнение 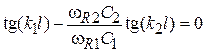, решить которое проще всего графически в любой математической программе. По найденному 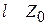находится из выражения 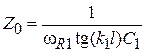. В данном случае эквивалентная индуктивность КК представляет собой последовательное соединение емкости варикапа 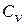и сосредоточенной индуктивности L. Заменяя индуктивность резонатором, получаем на частоте 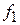уравнени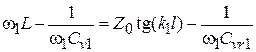е: , где 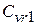‒ емкость варикапа, обеспечивающая выполнение равенства. Такое же уравнение можно записать для частоты 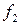: 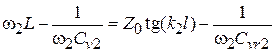. Из этих уравнений получаем трансцендентное уравнение для определения длины КР 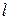: 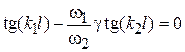, где 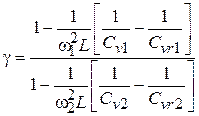. Решая уравнение графическим путем, находим длину 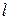. Волновое сопротивление находим из уравнения 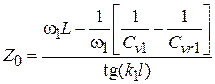. Перейдем теперь к вопросу о фазовых шумах. Фазовые шумы (ФШ) являются одним из важнейших параметров АГ. Эти шумы образуются вследствие преобразования шумовых напряжений, создаваемых активным элементом АГ и активными сопротивлениями его схемы, в фазомодулированные колебания. Преобразование происходит на реактивных элементах, зависящих от напряжения (варикапы, емкости транзисторов и диодов). Наибольшими ФШ обладают ГУН с управляющим элементом в виде варикапа. Уровень фазовых шумов зависит от производной 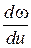, где 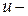управляющее напряжение на варикапе. Найдем значение этой производной для ГУН с сосредоточенной индуктивностью :

.

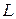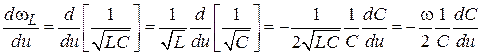Для ГУН с КР: .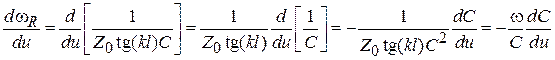

Сравнивая оба эти выражения, приходим к выводу, что для ГУН с КР абсолютное значение производной в 2 раза больше, чем для ГУН с сосредоточенной индуктивностью. Это значит, что при прочих равных условиях уровень фазовых шумов для ГУН с КР на 6 дБн выше, чем для ГУН с сосредоточенной индуктивностью (дБн ‒ уровень по отношению к уровню несущей частоты).

Интервал изменения частоты в ГУН с отрезком ЛП в качестве индуктивности будет всегда меньше, нежели для ГУН с сосредоточенной индуктивностью. Чем больший угол 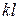выбран на нижней частоте, тем меньше достижимое изменение частоты при той же вариации емкости варикапа.