Принципы и виды математического моделирования

Математические модели должны обладать следующими свойствами:

1. адекватность, свойство соответствия модели и объекта исследований;

2. достоверность, обеспечение заданной вероятности попадания результатов моделирования в доверительный интервал,

3. точность, незначительное (в пределах допустимой погрешности) расхождение результатов моделирования с показателями реальных объектов (процессов);

4. устойчивость, свойство соответствия малых изменений выходных параметров малым изменениям входных;

5. эффективность, способность достижения цели с малыми затратами ресурсов;

6. адаптабельность, способность легко перестраиваться для решения различных задач.

Для достижения этих свойств существуют некоторые принципы (правила) математического моделирования [], ряд которых приведен ниже.

1. Принцип целенаправленности заключается в том, что модель должна обеспечивать достижение строго определенных целей и, в первую очередь, отражать те свойства оригинала, которые необходимы для достижения цели.

2. Принцип информационной достаточности заключается в ограничении количества информации об объекте при создании его модели и поиске оптимума между вводимой информацией и результатами моделирования. Он может быть проиллюстрирован следующей схемой.

Все возможные случаи моделирования располагаются в столбце 2.

3. Принцип осуществимости состоит в том, что модель должна обеспечивать достижение поставленной цели с вероятностью близкой к 1 и за конечное время. Этот принцип можно выразить двумя условиями

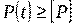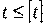и ,(1)

где 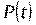- вероятность достижения цели, 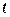- время достижения цел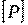и, и 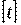- допустимые значения вероятности и времени достижения цели.

4. Принцип агрегатирования заключается в том, что модель должна состоять из подсистем 1-го уровня, которые, в свою очередь, состоят из подсистем 2-го уровня и т.д. Подсистемы должны оформляться в виде отдельных самостоятельных блоков. Подобное построение модели позволяет использовать стандартные процедуры расчетов, а также делает более легкой адаптацию модели к решению различных задач.

5. Принцип параметризации состоит в замене при моделировании определенных параметров подсистем, описанных функциями, соответствующими числовыми характеристиками.

Процесс моделирования с использованием этих правил заключается в выполнении следующих 5 шагов (этапов).

1. Определение целей моделирования.

2. Разработка концептуальной модели (расчетной схемы).

3. Формализация.

4. Реализация модели.

5. Анализ и интерпретация результатов моделирования.

Существенные различия в выполнении 3-5 этапов позволяют говорить о двух подходах к построению модели.

Аналитическое моделирование – это использование математической модели в виде дополненных системой ограничений уравнений, связывающих входные переменные с выходными параметрами. Аналитическое моделирование используется, если существует законченная постановка задачи на исследования и необходимо получить один конечный результат, соответствующий ей.

Имитационное моделирование – это использование математической модели для описания функционирования системы во времени при различных сочетаниях параметров системы и различных внешних воздействиях. Имитационное моделирование используется, если конечной постановки задачи не существует и необходимо исследовать протекающие в системе процессы. Имитационное моделирование предполагает соблюдение временного масштаба. Т.е. события на модели происходят через интервалы времени пропорциональные событиям на оригинале с постоянным коэффициентом пропорциональности.

По использованию средств для реализации модели можно выделить еще один вид моделирования, компьютерное моделирование. Компьютерное моделирование – это математическое моделирование с использованием средств вычислительной техники.