Понятия пространства и времени и их основные свойства

Естественнонаучные представления о пространстве и времени прошли длительный путь становления и развития. В материалистической картине мира понятие пространства возникло на основе наблюдения и практического использования объектов, их объема и протяженности. Понятие времени возникло на основе восприятия человеком смены событий, последовательной смены состояний предметов и круговорота различных процессов. Обыденные представления о пространстве и времени рассматривали их как внешние условия бытия, в которые помещена материя и которые сохранились бы, даже если бы материя исчезла.

Наиболее отчетливо концепцию абсолютного пространства и абсолютного времени сформулировал И. Ньютон в работе «Математические начала натуральной философии». По Ньютону пространство и время составляют как бы вместилища самих себя и всего существующего, представляют собой самодовлеющие элементы бытия, существующие вне и независимо от любых материальных процессов, это некоторые универсальные условия, в которые помещена материя.

Развитие естествознания привело к принципиально другим толкованиям пространства и времени. Современное понимание пространства и времени сформулировано в теории относительности А. Эйнштейна. По Эйнштейну пространство и время – формы существования материи, не существующие вне материи, эти атрибуты материи определяются ее связями и взаимодействиями. Далее этот вопрос будет рассмотрен более подробно.

Всеобщими свойствами пространства и времени являются их объективность и независимость от человеческого сознания, проявление на всех структурных уровнях существования материи, неразрывная связь друг с другом и с движущейся материей. Невзирая на неразрывную связь между собой, пространство и время обладают рядом специфических свойств.

Рассмотрим основные свойства пространства.

1 Однородность – все точки пространства обладают одинаковыми свойствами, нет выделенных точек пространства, параллельный перенос системы координат не изменяет законов природы.

2 Изотропность – все направления в пространстве обладают одинаковыми свойствами, нет выделенных направлений; поворот системы координат на любой угол сохраняет неизменными законы природы.

3 Непрерывность – между двумя любыми различными точками в пространстве, как бы близко они не находились, всегда есть третья.

4 Трехмерность – каждая точка пространства однозначно определяется набором трех действительных чисел (координат).

5 Евклидовость – свойства пространства описываются геометрией Евклида.

Рассмотрим два последних свойства более подробно.

На глубокую связь между размерностью пространства и законом всемирного тяготения указывал еще И. Кант. Согласно теореме Эренфеста (1917), большинство взаимодействий убывает с расстоянием по закону F~1/r^n-1, где n – размерность пространства. Таким образом,трехмерность пространства приводит к тому, что в нашем мире работает «закон обратных квадратов», т.е. силы убывают пропорционально квадрату расстояния (сила гравитационного взаимодействия, сила взаимодействия электрических зарядов и т.д.). В четырехмерном пространстве (n=4) сила взаимодействия между планетами была бы обратно пропорциональна кубу расстояния между ними. В таком воображаемом мире планеты двигались бы по спиралям и быстро упали бы на Солнце. При числе измерений более трех не существовало бы и устойчивых электронных орбит в атомах, следовательно, не было бы химических процессов и жизни.

Установлено, что при распространении волн в пространстве с четным числом измерений наблюдаются искажения, нарушающие переносимую волной информацию. Пример тому – распространение волны по резиновому покрытию (n=2). Г. Дж. Уитроу (1955 г.) пришел к выводу, что поскольку живым организмам необходимы передача и обработка информации, то высшие формы жизни не могут существовать в пространстве четной размерности. Следует отметить, указанные выводы относятся к известным нам законам природы и формам жизни и не исключают существование миров иной природы.

Согласно Оксфордскому толковому словарю, геометрия – это наука о свойствах и отношениях величин в пространстве. Древнегреческий математик Евклид (около 330-275 до н.э.) создал стройное учение о свойствах пространства, т.н. евклидову геометрию, которая практически в неискаженном виде до сих пор входит в школьный курс. Геометрия Евклида основана на 10 постулатах (утверждений, истинность которых считается очевидной и принимается на веру). Все остальное покоится на этих постулатах как здание на своем фундаменте. Если изменить постулаты, то изменится и весь предмет, что на них основан. В геометрии Евклида постулируется, что линия, вдоль которой расстояние между двумя точками M и N минимально, есть прямая; касательная к этой линии не меняет своего направления от точки к точке. Постулат Евклида о параллельных утверждает, что через точку Р можно провести одну и только одну прямую, параллельную заданной прямой MN, не содержащей точки Р (рисунок 1).

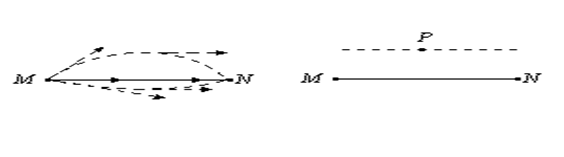
Рисунок 1 – Понятие прямой в геометрии Евклида

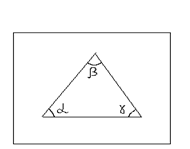
Сумма углов треугольника в пространстве Евклида равна 180°, отношение длины окружности к ее диаметру равно π.

Пространство с такими свойствами называется плоским или пространством с нулевой кривизной (R=0). Плоскому пространству соответствует т.н. евклидова метрика

dl² = dx² + dy² + dz². (2.1)

Физика Ньютона опирается на геометрию Евклида, т.е. это физика плоского пространства.

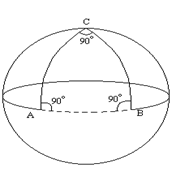
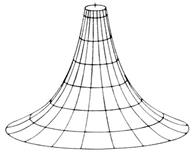
Примером двумерного плоского пространства служит лист бумаги. Легко представить искривленное двумерное пространство: поверхность сферы или поверхность горлышка кувшина в самой узкой его части. Первый пример относится к классу поверхностей с положительной кривизной (R>0), второй – к классу поверхностей с отрицательной кривизной (R<0). Геометрия искривленного пространства с положительной кривизной была создана в 60-х годах XIX в. Б. Риманом. Н.И. Лобачевский и Я. Больяй разработали геометрию пространства с отрицательной кривизной.

На поверхности с положительной кривизной нельзя провести ни одной прямой, параллельной данной; сумма углов треугольника больше 180º. В геометрии Лобачевского и Больяй постулируется, что через заданную точку в пространстве с отрицательной кривизной можно провести сколько угодно прямых параллельных данной. Сумма внутренних углов треугольника на поверхности с отрицательной кривизной меньше 180º. Примеры двумерных пространств с разной кривизной представлены на рисунке 2.

Понятия плоского и искривленного пространства можно обобщить на случай более двух измерений. Эйнштейн показал, что кривизна пространства обуславливается гравитирующей массой, геометрия реального пространства-времени всегда неевклидова.

R=0	R>0	R<0
Рисунок 2 – Примеры двумерных пространств с разной кривизной

Рассморим основные свойства времени.

1 Однородность – любые явления, происходящие в одних и тех же условиях, но в разное время, протекают одинаково.

2 Непрерывность – между двумя различными моментами времени, как бы близко они не находились, всегда можно выделить третий.

3 Одномерностьвремени проявляется в линейной последовательности событий, генетически связанных между собой. Если для определения положения точки в пространстве необходимо задать три координаты (пространство трехмерно), то для определения времени достаточно одной.

4 Необратимость – однонаправленное изменение от прошлого к настоящему и от настоящего к будущему, но никогда наоборот.

Перечисленные свойства пространства и времени определяют характер физических законов. Симметрия времени (связанная с его однородностью) и симметрия пространства (связанная с его однородностью и изотропностью) приводят к фундаментальным законам сохранения энергии, импульса и момента импульса. Необратимость времени связана со вторым законом термодинамики. Эти вопросы будут рассмотрены позднее.