Принцип эквивалентности сил инерции и тяготения
Законы Ньютона выполняются только в инерциальных системах отсчета, т.е. системах отсчета, движущихся равномерно и прямолинейно. Легко привести примеры невыполнения этих законов в неинерциальных СО (например, в тормозящем автобусе, в набирающем скорость на взлетном полосе самолете и т.д.). Любая неинерциальная СО движется относительно инерциальных систем отсчета с некоторым ускорением, поэтому ускорение тела в неинерциальной СО отлично от ускорения тела в инерциальных системах отсчета (одинакового во всех). Обозначим разность ускорений тела в неинерциальной и инерциальной системах отсчета через 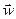 .
.
При описании движения в неинерциальных СО можно пользоваться уравнениями Ньютона, если наряду с силами, обусловленными воздействием тел друг на друга, учитывать т.н. силы инерции. Силы инерции полагают равными произведению массы тела на взятую с обратным знаком разность его ускорений по отношению к инерциальной и неинерциальной системам отсчета
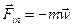 . (2.5)
. (2.5)
Соответственно, второй закон Ньютона в неинерциальной системе отсчета будет иметь вид
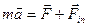 . (2.6)
. (2.6)
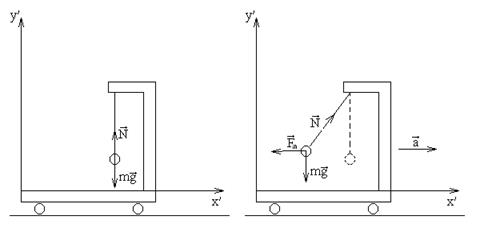 |
Сказанное можно пояснить простым примером. Рассмотрим тело, подвешенное к потолку вагона (рисунок 3).
Рисунок 3 – Возникновение силы инерции
в неинерциальной системе отсчета
Если вагон находится в состоянии покоя или движется равномерно и прямолинейно, то он является инерциальной системой отсчета и второй закон Ньютона для тела имеет вид
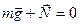 .(2.7)
.(2.7)
Пусть теперь вагон движется поступательно с ускорением 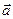 и является неинерциальной СО. Нить отклонится от вертикали на такой угол α, чтобы результирующая сил тяжести и натяжения нити
и является неинерциальной СО. Нить отклонится от вертикали на такой угол α, чтобы результирующая сил тяжести и натяжения нити 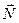 сообщали телу ускорение
сообщали телу ускорение 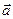 . Отсутствие ускорения тела в СО, связанной с вагоном, формально можно связать с тем, что на шарик еще действует сила инерции
. Отсутствие ускорения тела в СО, связанной с вагоном, формально можно связать с тем, что на шарик еще действует сила инерции 
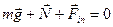 .(2.8)
.(2.8)
Введение сил инерции дает возможность описывать движение тел в любых (как инерциальных, так и неинерциальных) системах отсчета с помощью одних и тех же уравнений движения. Силы инерции обусловлены не взаимодействием тел, а свойствами той СО, в которой рассматриваются механические явления. В этом смысле силы инерции называют фиктивными силами.
Характерным свойством сил инерции является их пропорциональность массе тела, благодаря чему они оказываются аналогичными силам тяготения. Представим себе, что мы находимся в закрытой кабине, которая движется с ускорением - 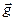 в направлении, которое мы условно назовем «верхом». Тогда все тела, находящиеся внутри кабины, будут вести себя так, как будто на них действует сила инерции
в направлении, которое мы условно назовем «верхом». Тогда все тела, находящиеся внутри кабины, будут вести себя так, как будто на них действует сила инерции  . В частности, пружина, к концу которой подвешено тело массой m, растянется так, чтобы упругая сила уравновесила силу инерции
. В частности, пружина, к концу которой подвешено тело массой m, растянется так, чтобы упругая сила уравновесила силу инерции  . Однако такие же явления наблюдались бы, если бы кабина была неподвижной и находилась вблизи поверхности Земли. Находясь внутри закрытой кабины, никакими опытами нельзя установить, чем вызвано действие на тело силы
. Однако такие же явления наблюдались бы, если бы кабина была неподвижной и находилась вблизи поверхности Земли. Находясь внутри закрытой кабины, никакими опытами нельзя установить, чем вызвано действие на тело силы  : тем, что кабина движется с ускорением -
: тем, что кабина движется с ускорением - 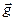 , или тем, что кабина находится вблизи гравитирующей массы (например, планеты Земля). Все явления, которые обусловлены неинерциальностью системы отсчета, могут наблюдаться и в инерциальной системе в результате действия сил тяготения. На этом основании говорят об эквивалентности сил инерции и тяготения. Следствием этой эквивалентности является тождественность инертной и гравитационной масс.
, или тем, что кабина находится вблизи гравитирующей массы (например, планеты Земля). Все явления, которые обусловлены неинерциальностью системы отсчета, могут наблюдаться и в инерциальной системе в результате действия сил тяготения. На этом основании говорят об эквивалентности сил инерции и тяготения. Следствием этой эквивалентности является тождественность инертной и гравитационной масс.
Масса фигурирует в двух различных законах: основном законе динамики (втором законе Ньютона) и законе всемирного тяготения
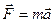 ;
; 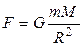 .(2.9)
.(2.9)
В первом случае она характеризует инертные свойства тела, во втором – гравитационные. Возникает вопрос: следует ли различать инертную и гравитационные массы? Совокупность опытных данных показывает, что инертная и гравитационная массы всех тел строго пропорциональны друг другу, что означает, что при надлежащем выборе единиц инертная и гравитационная массы становятся тождественными. Поэтому в физике говорят просто о массе.
Итак, согласно принципу эквивалентности свойства движения в неинерциальной СО такие же, как и в инерциальной при наличии гравитационного поля. В более широком смысле эквивалентность сил инерции и сил гравитации означает, что все физические, химические и биологические процессы в неинерциальных системах отсчета протекают по тем же законам, что и в гравитационном поле той же силы и направления. Таким образом, неинерциальная система отсчета эквивалентна некоторому гравитационному полю.
Дата добавления: 2017-10-09; просмотров: 1561;
