Основные типы трендов и методы их распознавания.
В данном разделе рассматриваются основные типы тенденций фондовых переменных, их свойства, отражаемые с большей или меньшей степенью полноты уравнением линии тренда. В отличие от простых систем механики тенденции изменения показателей сложных социальных, экономических, биологических и технических систем только с некоторым приближением отражаются тем или иным уравнением, линией тренда.
В этой лекции рассматриваются далеко не все известные в математике линии и их уравнения, а лишь набор сравнительно простых форм, который считается достаточным для отображения и анализа большинства встречающихся на практике тенденций временных рядов. При этом желательно всегда выбирать из нескольких типов линий, достаточно близко выражающих тенденцию, более простую зависимость. Этот «принцип простоты» обоснован тем, что чем сложнее уравнение линии тренда, чем большее число параметров оно содержит, тем при равной степени приближения труднее дать надежную оценку этих параметров по ограниченному числу уровней ряда и тем больше ошибка оценки этих параметров, ошибки прогнозируемых уровней.
7.1. Прямолинейный тренд и его свойства.
Самым простым типом линии тренда является прямая линия, описываемая линейным (т.е. первой степени) уравнением тренда:
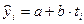 (7.1),
(7.1),
где 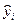 , - выравненные, т.е. лишенные колебаний, уровни тренда для года с номером i; а - свободный член уравнения, численно равный среднему выравненному уровню для момента или периода времени, принятого за начало отсчета, т.е. для t = 0; b - средняя величина изменения уровней ряда за единицу изменения времени;
, - выравненные, т.е. лишенные колебаний, уровни тренда для года с номером i; а - свободный член уравнения, численно равный среднему выравненному уровню для момента или периода времени, принятого за начало отсчета, т.е. для t = 0; b - средняя величина изменения уровней ряда за единицу изменения времени; 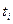 - момент времени.
- момент времени.
Среднее изменение уровней ряда за единицу времени - главный параметр и константа прямолинейного тренда. Следовательно, этот тип тренда подходит для отображения тенденции примерно равномерных изменений уровней: равных в среднем абсолютных приростов или абсолютных сокращений уровней за равные промежутки времени. Практика показывает, что такой характер динамики встречается достаточно часто. Причина близких к равномерному абсолютных изменений уровней ряда состоит в следующем: многие явления, как, например, урожайность сельскохозяйственных культур, численность населения региона, города, сумма дохода населения, среднее потребление какого-либо продовольственного товара и др., зависят от большого числа различных факторов. Одни из них влияют в сторону ускоренного роста изучаемого явления, другие - в сторону замедленного роста. Влияние разнонаправленных и разноускоренных (замедленных) сил факторов взаимно усредняется, частично взаимно погашается, а равнодействующая их влияний приобретает характер, близкий к равномерной тенденции. Итак, равномерная тенденция динамики (или застоя) - это результат сложения влияния большого количества факторов на изменение изучаемого показателя.
Графическое изображение прямолинейного тренда - прямая линия в системе прямоугольных координат с линейным (арифметическим) масштабом на обеих осях. Пример линейного тренда дан на рис. 7.1.
Абсолютные изменения уровней в разные годы не были точно одинаковыми, но общая тенденция сокращения численности занятых в народном хозяйстве очень хорошо отражается прямолинейным трендом.
Основные свойства тренда в форме прямой линии таковы:
• равные изменения за равные промежутки времени;
• если средний абсолютный прирост - положительная величина, то относительные приросты или темпы прироста постепенно уменьшаются;
• если среднее абсолютное изменение - отрицательная величина, то относительные изменения или темпы сокращения постепенно увеличиваются по абсолютной величине снижения к предыдущему уровню;
• если тенденция к сокращению уровней, а изучаемая величина является по определению положительной, то среднее изменение bне может быть больше среднего уровня а;
• при линейном тренде ускорение, т.е. разность абсолютных
изменений за последовательные периоды, равно пулю.
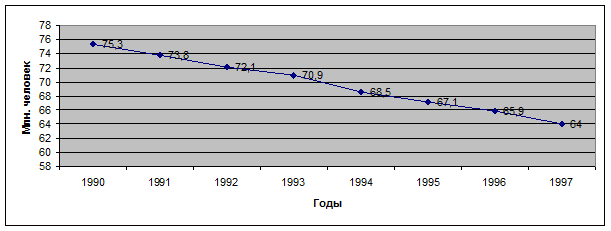
Рис. 7.1. Динамика числа занятых в народном хозяйстве в России на 31 декабря каждого года.
Свойства линейного тренда иллюстрирует табл. 7.1. Уравнение тренда:
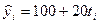 .
.
Показатели динамики при наличии тенденции сокращения уровней приведены в табл. 7.2.
Таблица 7.1.
Показатели динамики при линейном тренде к увеличению уровней: 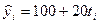 .
.
Номер
периода 
| Уровень 
| Абсолютное изменение к предыдущему периоду | Темпы (цепные), % | Ускорение |
| +20 | 120,0 | |||
| +20 | 1 16.7 | |||
| + 20 | 114.3 | |||
| +20 | 112.5 | |||
| + 20 | 1 1 1.1 | |||
| +20 | 110.0 |
Таблица 7.2.
Показатели динамики при линейном тренде сокращения уровней: 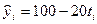
Номер периода 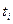
| Уровень 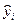
| Абсолютное изменение к предыдущему периоду | Темп к предыдущему периоду, % | Ускорение |
| -20 | 90,0 | - | ||
| -20 | 88,9 | |||
| -20 | 87,5 | |||
| -20 | 85,7 | |||
| -20 | 83,3 | |||
| 6 | -20 | 80,0 |
При изучении методов распознавания типа тренда не следует забывать о существе изучаемого процесса, который отображается временным рядом. Как правило, тип тренда должен соответствовать характерным особенностям процесса. В предыдущих разделах этой главы для каждого типа тренда приведены примеры выражаемых этим типом процессов. Определяя другие процессы по временным рядам, полезно по указанным примерам подобрать подходящие типы тренда. Практика всегда гораздо богаче, разнообразна любых гипотез и теорий: фактические временные ряды, особенно относящиеся к отдельным предприятиям, малоинерционным системам или к ограниченным отрезкам времени, могут и не соответствовать тем классическим трендам, которые приведены в этом разделе. Кроме того, характер тенденции часто маскируется значительной колеблемостью уровней ряда, поэтому требуется специальная методика распознавания типа тренда, наилучшим образом отражающего тенденцию фактического ряда уровней. После определения типа тренда необходимо вычислить оценки его параметров, как правило, по методу наименьших квадратов, а также с использованием специфических приемов для логарифмического или логистического типа тренда.
Графическое изображение во многих случаях позволяет приближенно выявить тип тенденции временного ряда. Но для этого следует соблюдать правила построения графика: точное соблюдение масштаба как по величине уровней ряда, так и по времени. Временные интервалы откладывают по оси абсцисс, величины уровней - по оси ординат. По каждой оси следует установить такой масштаб, чтобы ширина графика была примерно в 1,5 раза больше его высоты. Если уровни ряда на всем протяжении периода много больше нуля и между собой различаются не более чем на 20-30%, то следует обозначить перерыв на оси ординат, увеличить масштаб так, чтобы меньший из уровней ненамного превышал разрыв оси. Если уровни ряда различаются в десятки, сотни и тысячи раз, ось ординат следует разметить в логарифмическом масштабе, чтобы равные отрезки означали различие уровней в одинаковое число раз. Интерпретация вида графика будет другой: при линейном масштабе график, близкий к прямой линии, означает линейную тенденцию, а при логарифмическом масштабе оси ординат прямая линия показывает экспоненциальную тенденцию.
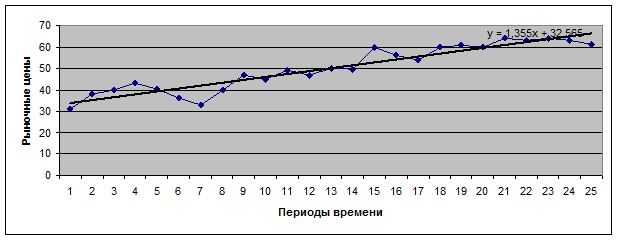 Рис. 7.2. Динамика рыночной цены некоторой акции.
Рис. 7.2. Динамика рыночной цены некоторой акции.
Необходимо строго соблюдать равенство промежутков времени на равных отрезках оси абсцисс. Логарифмический масштаб по времени не рекомендуется, так как он крайне затруднит интерпретацию графика. Рассмотрим пример графического изображения, представленного на рис. 7.2. Из рисунка видно, что линейный тренд хорошо подходит для отражения тенденции динамики изменения рыночной цены акции: прямая проходит как бы посреди колеблющихся точек – дневных уровней.
Но не всегда график позволяет выбрать тип линии тренда. Трудно графически отличить параболу от экспоненты, логарифмическую кривую от гиперболы и т.д. Оценка типа тренда по тину графика включает субъективные моменты, что может привести к ошибке. Есть много способов объективной, статистико-математической оценки пригодности того или иного типа липни. Весьма популярен его выбор с помощью перебора на электронных вычислительных машинах (ЭВМ) всех имеющихся в пакете программ статистического анализа типов линий либо по наименьшему среднему квадратическому отклонению, либо по наименьшему модулю отклонений фактических уровней от расчетных по проверяемой линии. Недостатки данной методики заключаются в том, что, во-первых, не все пакеты программ статистического анализа содержат достаточный выбор линий тренда, но главное состоит в том, что, как уже указано в предыдущей главе, чем больше параметров содержит уравнение тренда, тем меньше и отклонений отдельных уровней от тренда. Парабола II порядка, а тем более III и более высоких порядков всегда при таком подходе «лучше», чем прямая или экспонента.
Но «преимущество» параболы над прямой может быть невелико. Следовательно, нужно применить опять же математические критерии существенности уменьшения среднего отклонения при переходе от прямой к параболе. Не отрицая допустимости указанной методики с дополнительной проверкой существенности снижения среднего отклонения от тренда, рассмотрим и другие методы выбора типа тренда без вычисления последнего, а также средних отклонений.
Данные виды трендов объединены в связи с тем, что методика оценки их параметров имеет много общего. Основой этой методики служит метод наименьших квадратов, который дает оценки параметров, отвечающие принципу максимального правдоподобия: сумма квадратов отклонений фактических уровней от тренда (от выравненных по уравнению тренда уровней) должна быть минимальной для данного типа уравнения.
Эта методика близка к методике корреляционно-регрессионного анализа связей - парной регрессии. Однако между ними есть и принципиальные различия: выступающий при расчете уравнения тренда в качестве независимой переменной ряд номеров периодов или моментов времени не является случайной варьирующей переменной X регрессионного анализа. Ряд значений времени - это жестко упорядоченный ряд величин, и, следовательно, не может быть речи о корреляции между ним и значениями зависимой переменной - варьирующих уровней показателя, изменяющегося во времени. Нередко применяемые в литературе и в программах ЭВМ коэффициенты корреляции со временем или фактических уровней с выравненными (т.е. тоже упорядоченными) уровнями тренда таковыми на самом деле не являются и не могут измерять какой-либо «тесноты связи». Чем длиннее период, охватываемый рядом, тем автоматически становятся больше так называемые коэффициенты корреляции при той же самой скорости роста уровней и той же самой силе колебаний. Таким образом, эти лжекоэффициенты не могут характеризовать соотношение между ролью факторов тенденции и ролью факторов колеблемости.
Величины параметров aи bв уравнении прямой линии (7.1) определяются по методу наименьших квадратов путем приравнивания частных первых производных функции
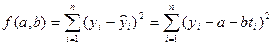 (7.2)
(7.2)
к нулю:
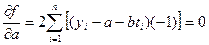 (7.3),
(7.3),
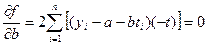 (7.4).
(7.4).
После алгебраических преобразований получаем два «нормальных уравнения» метода наименьших квадратов (МНК) для прямой:
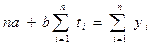 (7.5),
(7.5),
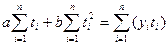 (7.6).
(7.6).
Решая эти уравнения с двумя неизвестными по данным фактического временного ряда 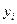 ,получаем значения «a»и «b». Если номера периодов (моментов) времени отсчитываются от начала ряда так, что первый период (момент) обозначен номером t = 1, то свободный член «а»есть уровень тренда для предыдущего периода (момента), а не первого в ряду, как часто ошибочно полагают. Для первого периода уровень тренда равен (a+b), для второго у2 = (а+2b) и т.д.
,получаем значения «a»и «b». Если номера периодов (моментов) времени отсчитываются от начала ряда так, что первый период (момент) обозначен номером t = 1, то свободный член «а»есть уровень тренда для предыдущего периода (момента), а не первого в ряду, как часто ошибочно полагают. Для первого периода уровень тренда равен (a+b), для второго у2 = (а+2b) и т.д.
Однако рациональнее начало отсчета времени перенести в середину ряда, т.е. при нечетном n -на период (момент) с номером (n+ 1 )/2, а при четном числе уровней ряда - на середину между периодом с номером n/2 и (n/2)+1. В последнем случае все номера периодов  будут дробными. При нумерации периодов времени точно от середины ряда половина номеров
будут дробными. При нумерации периодов времени точно от середины ряда половина номеров  будет отрицательными числами (аналогично годам до нашей эры), а половина - положительными, т.е.
будет отрицательными числами (аналогично годам до нашей эры), а половина - положительными, т.е. 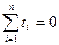 . В таком случае система нормальных уравнений МНК распадается на два уравнения с одним неизвестным в каждом:
. В таком случае система нормальных уравнений МНК распадается на два уравнения с одним неизвестным в каждом:
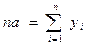 (7.7)
(7.7)
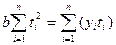 (7.8).
(7.8).
Откуда имеем:
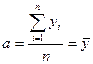 (7.9);
(7.9);
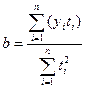 (7.10).
(7.10).
К сожалению, многие компьютерные программы не предусматривают такого упрощения, и нумерация периодов (моментов) в них производится с начала ряда, с номера t = 1,причем пользователь об этом не предупреждается.
Приведем расчет линейного тренда по временному ряду (см. рис. 7.1). Динамика численности занятых в народном хозяйстве России с 1990 по 1996 г. представлена в табл. 7.3. В целях экономии места в той же таблице приведены и другие показатели, необходимые для измерения колеблемости.
Таблица 7.3.
Расчет линейного тренда
| Год | Уровень, 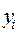 млн. чел. млн. чел.
| Номер года, 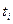
| 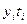
| Тренд
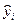 млн. чел.
млн. чел.
| Отклонение от тренда,
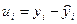
|
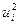
| 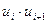
| |
| . | ||||||||
| 75,3 | -3 | -225,9 | 75,3 | 0,0 | 0,00 | 0,00 | ||
| 73,8 | -2 | -147,6 | 73,7 | 0,1 | 0,01 | 0,00 | ||
| 72,1 | -1 | -72,1 | 72,1 | 0,0 | 0,00 | 0,00 | ||
| 70,9 | 0,0 | 70,5 | 0,4 | 0,16 | -0,16 | |||
| 68,5 | 68,5 | 68,9 | -0,4 | 0,16 | 0,08 | |||
| 67,1 | 134,2 | 67,3 | -0,2 | 0,04 | -0,04 | |||
| 65,9 | 197,7 | 65,7 | 0,2 | 0,04 | — | |||
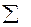
| 493,6 | -45,2 | 493,5 | 0,1 | 0,41 | -0,12 | ||
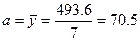 млн. чел.;
млн. чел.; 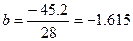 млн. чел. В год.
млн. чел. В год.
Уравнение тренда: 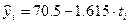 ,
, 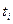 = 0 в 1993 г. В среднем численность занятых сокращалась на 1615 тыс. чел. в год. Сумма уровней тренда должна равняться сумме фактических уровней, различие в четвертой значащей цифре связано с округлением значений параметров.
= 0 в 1993 г. В среднем численность занятых сокращалась на 1615 тыс. чел. в год. Сумма уровней тренда должна равняться сумме фактических уровней, различие в четвертой значащей цифре связано с округлением значений параметров.
7.2. Параболический тренд и его свойства.
Под названием параболического будем иметь в виду тренд, выраженный параболой II порядка с уравнением:
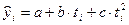 (7.11).
(7.11).
Параболы III порядка и более высоких порядков редко применимы для выражения тенденции динамики и слишком сложны для получения надежных оценок параметров при ограниченной длине временного ряда. Прямую линию, с точки зрения математики, можно также считать одним из видов парабол - параболой I порядка, которая уже рассмотрена ранее.
Значения параметров параболы II порядка таковы: свободный член а - это средний (выравненный) уровень тренда на момент или период, принятый за начало отсчета времени, т.е. t = 0; b - это средний за весь период среднегодовой прирост, который уже не является константой, а изменяется равномерно со средним ускорением, равным 2с, которое и служит константой, главным параметром параболы II порядка.
Следовательно, тренд в форме параболы II порядка применяется для отображения таких тенденций динамики, которым свойственно примерно постоянное ускорение абсолютных изменений уровней. Процессы такого рода встречаются на практике гораздо реже, чем процессы с равномерным изменением, но, с другой стороны, любое отклонение процесса от строго равномерного прироста (или сокращения) уровней можно интерпретировать как наличие ускорения. Более того, существует строгое математическое правило: чем выше порядок параболы, тем ближе линия тренда к уровням исходного временного ряда. Если это правило довести до крайнего предела, то любой ряд из п уровней может быть точно отображен параболой (n-1)-гопорядка! (Через любые две точки проходит одна прямая, через три точки - одна парабола II порядка и т.д.) Такое «приближение» линий тренда к эмпирическому ряду, содержащему как тенденцию, так и колебания, нельзя считать достижением научного анализа. Напротив, применяя параболу более высокого порядка там, где сущность процесса этого не требует, а только ради уменьшения остаточной суммы отклонений (или их квадратов) отдельных уровней от тренда, исследователь уходит от цели, смешивая тренд с колебаниями.
Парабола II порядка, как уравнение тренда, применяется к различным процессам, которые на некотором, как правило, непродолжительном, этапе развития имеют примерно постоянное ускорение абсолютного прироста уровней. Такими бывают рост населения отдельных городов или регионов, ускоренное увеличение объема продукции в фазе циклического подъема, как, например, динамика экспорта Японии в 1988-1995 гг., приведенная на рис. 7.3.
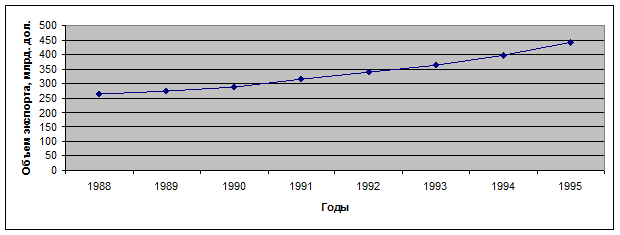
Рис. 7.3. Динамика экспорта Японии.
Основные свойства тренда в форме параболы II порядка таковы:
1) неравные, но равномерно возрастающие или равномерно
убывающие абсолютные изменения за равные промежутки времени;
2) парабола, рассматриваемая относительно ее математической формы, имеет две ветви: восходящую с увеличением уровней признака и нисходящую с их уменьшением. Но относительно статистики по содержанию изучаемого процесса изменений трендом, выражающим определенную тенденцию развития, чаще всего можно считать только одну из ветвей: либо восходящую, либо нисходящую. В особых, более конкретных, ситуациях мы не отрицаем возможности объединения
обеих ветвей в единый тренд;
3) так как свободный член уравнения «а» как значение показателя в начальный момент (период) отсчета времени, как правило, величина положительная; то характер тренда определяется знаками параметров b и с:
а) при b>0 и с>0 имеем восходящую ветвь, т.е. тенденцию к
ускоренному росту уровней;
б) при b<0 и с<0 имеем нисходящую ветвь - тенденцию к
ускоренному сокращению уровней:
в) при b>0 и с<0 имеем либо восходящую ветвь с замедляющимся ростом уровней, либо обе ветви параболы, восходящую и нисходящую, если их по существу можно считать единым процессом;
г) при b<0 и с>0 имеем либо нисходящую ветвь с замедляющимся сокращением уровней, либо обе ветви - нисходящую и восходящую, если их можно считать единой тенденцией;
4) при параболической форме тренда, в зависимости от соотношений между его параметрами, цепные темпы изменений могут либо уменьшаться, либо некоторое время возрастать, но при достаточно длительном периоде рано или поздно темпы роста обязательно начинают уменьшаться, а темпы сокращении уровней при b<0 и с<0 обязательно начинают возрастать.
Ввиду ограниченного объема лекционного материала рассмотрим не все четыре случая параболических трендов, а лишь два первых (табл. 7.4 и 7.5).
Таблица 7.4.
Показатели динамики при параболическом тренде, когда b>0, с>0: 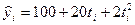 .
.
Номер периода 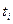
| Уровень 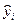
| Абсолютное изменение к предыдущему периоду | Цепные темпы, % к предыдущему | Ускорение |
| +22 | - | |||
| +26 | 121.3 | +4 | ||
| +30 | 120.3 | +4 | ||
| +34 | 119.1 | +4 | ||
| +38 | 117.9 | +4 | ||
| +42 | 116.8 | +4 |
Таблица 7.5.
Показатели динамики при параболическом тренде, когда b<0, с<0: 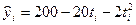 .
.
Номер периода 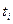
| Уровень 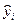
| Абсолютное изменение к предыдущему периоду | Цепные темпы, % к предыдущему | Ускорение |
| -22 | - | |||
| -26 | 85.4 | -4 | ||
| -30 | 80.3 | -4 | ||
| -34 | 72.1 | -4 | ||
| -38 | 56.8 | -4 | ||
| -42 | -4 |
В тех случаях, когда по существу изучаемого процесса допустимо считать единым трендом обе ветви параболы, представляет большой интерес решение задачи о нахождении того периода или момента времени, когда уровень тренда достигает максимума (когда b>0, с<0) или минимума (если b<0, с>0). Экстремальная точка параболы 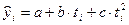 достигается при нулевом значении первой производной этой функции по времени:
достигается при нулевом значении первой производной этой функции по времени:
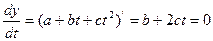 или
или 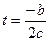
Например, если у = 100 + 20t – 2t 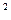 , то максимум парабола имеет при
, то максимум парабола имеет при 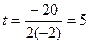 .
.
Для вычисления параметров a, b, c по методу наименьших квадратов три частные производные функции: 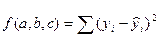 приравниваются к нулю, и после преобразований получаем систему трех уравнений с тремя неизвестными:
приравниваются к нулю, и после преобразований получаем систему трех уравнений с тремя неизвестными:
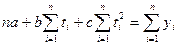 (7.12)
(7.12)
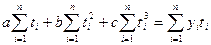 (7.13)
(7.13)
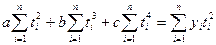 (7.14).
(7.14).
При переносе начала отсчета периодов (моментов) времени в середину ряда суммы нечетных степеней номеров этих периодов 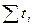 и
и 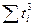 обращаются в нуль. При этом второе уравнение обращается в уравнение с одним неизвестным, откуда
обращаются в нуль. При этом второе уравнение обращается в уравнение с одним неизвестным, откуда 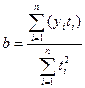 .
.
Уравнения (7.12) и (7.14) образуют систему двух уравнений с двумя неизвестными:
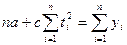 (7.15),
(7.15),
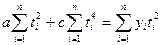 (7.16).
(7.16).
Приведем пример расчета параболического тренда по данным рис. 7.3 и табл. 7.6, в которой присутствуют также графы, необходимые для анализа колеблемости.
Таблица 7.6.
Расчет параболического тренда объема экспорта Японии.
| Год | Уровень,  млн. чел. млн. чел.
| Номер года, 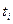
| 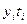
| 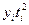
| Тренд
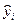 млн. чел.
млн. чел.
| Отклонение от тренда,
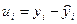
|
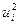
| 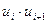
|
| -3.5 | -927.5 | -1 | ||||||
| -2.5 | -685.0 | -1 | ||||||
| -1.5 | -432.0 | -2 | -10 | |||||
| -0.5 | -157.5 | |||||||
| 0.5 | -170.0 | -15 | ||||||
| 1.5 | -543.0 | -3 | ||||||
| 2.5 | -992.5 | -4 | -4 | |||||
| 3.5 | 1550.5 | - | ||||||
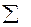
| 1054.0 |
Вычислим параметры параболы: 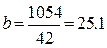 ;
; 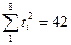 ;
; 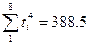
8a + 42c = 2684
42a + 388.5c = 14492.
Откуда а = 321.7; с = 2.4.
Уравнение тренда: 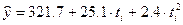 .
.
Интерпретация параметров тренда такова: экспорт Японии в 1988-1995 гг. возрастал в номинальной оценке ускоренно, со средним ускорением: 2*2,4 = 4,8 млрд. дол. в год за каждый год, средний за весь период прирост объема экспорта составил 25.1 млрд. дол. в год, средний уровень экспорта на середину периода был равен 321.7 млрд. дол.
7.3. Экспоненциальный тренд и его свойства.
Экспоненциальным трендом называют тренд, выраженный
уравнением:
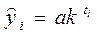 (7.17).
(7.17).
Свободный член экспоненты «а» равен выровненному уровню, т.е. уровню тренда в момент или период, принятый за начало отсчета времени, т.е. при t=0. Основной параметр экспоненциального тренда k является постоянным темпом изменения уровней (цепным). Если k>1, имеем тренд с возрастающими уровнями, причем это возрастание не просто ускоренное, а с возрастающим ускорением и возрастающими производными всех более высоких порядков. Если k<1, то имеем тренд, выражающий тенденцию постоянного, но замедляющегося сокращения уровней, причем замедление непрерывно усиливается. Экстремума экспонента не имеет и при 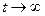 стремится либо к бесконечности при k>1, либо к 0 при k< 1.
стремится либо к бесконечности при k>1, либо к 0 при k< 1.
Экспоненциальный тренд характерен для процессов, развивающихся в среде, не создающей никаких ограничений для роста уровня. Из этого следует, что на практике он может развиваться только на ограниченном промежутке времени, так как любая среда рано или поздно создает ограничения, любые ресурсы со временем исчерпываются. Однако практика показала, что, например, численность населения Земли на протяжении 1950-1985 гг. возрастала примерно по экспоненте со среднегодовым темпом роста k=1.018 и за это время возросла вдвое – с 2.5 до 5 млрд. чел. (рис. 7.4). В настоящее время темп роста населения постепенно уменьшается.
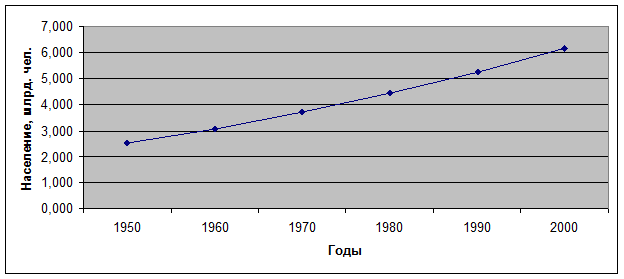 Рис. 7.4. Рост народонаселения Земли.
Рис. 7.4. Рост народонаселения Земли.
Экспоненциальный рост объема реализации и производства происходит при возникновении новых видов продукции и их освоении промышленностью: при появлении цветных телевизоров, видеомагнитофонов, пейджеров и т.п., но когда производство начинает наполнять рынок, приближаться к спросу, экспоненциальный рост прекращается.
Основные свойства экспоненциального тренда:
1. Абсолютные изменения уровней тренда пропорциональны самим уровням.
2. Экспонента экстремумов не имеет: при k>1 тренд стремится к 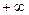 , при k< 1 тренд стремится к нулю.
, при k< 1 тренд стремится к нулю.
3. Уровни тренда представляют собой геометрическую прогрессию.
4. При k>1 тренд отражает ускоряющийся неравномерно рост уровней, при k<1 тренд отражает замедляющееся неравномерно уменьшение уровней.
Поведение основных показателей динамики в этих случаях рассмотрено в табл. 7.6 и 7.7.
В табл. 7.6 и 7.7 в последней графе приведены редко применяемые показатели динамики III порядка: ускорение (или прирост) ускорения и замедление ускорения. Эти абсолютные показатели даны для наглядного пояснения главного отличия экспоненциального тренда от парабол любого порядка: экспонента не имеет постоянных производных любого порядка по времени. Постоянен только цепной темп изменения.
Таблица 7.6.
Дата добавления: 2017-10-09; просмотров: 2564;
