Законы физики на примере качели

Не только пандусы, о которых мы говорили в разделе 1.3, дают выигрыш в силе. В данном разделе мы займемся еще одним похожим приспособлением — качеля­ми, которые представляют собой разновидность рычага. Изучая качели, мы вновь встретимся с уже знакомыми нам законами механики. Но теперь мы рассмотрим эти законы в ином контексте — в контексте вращательного движения.

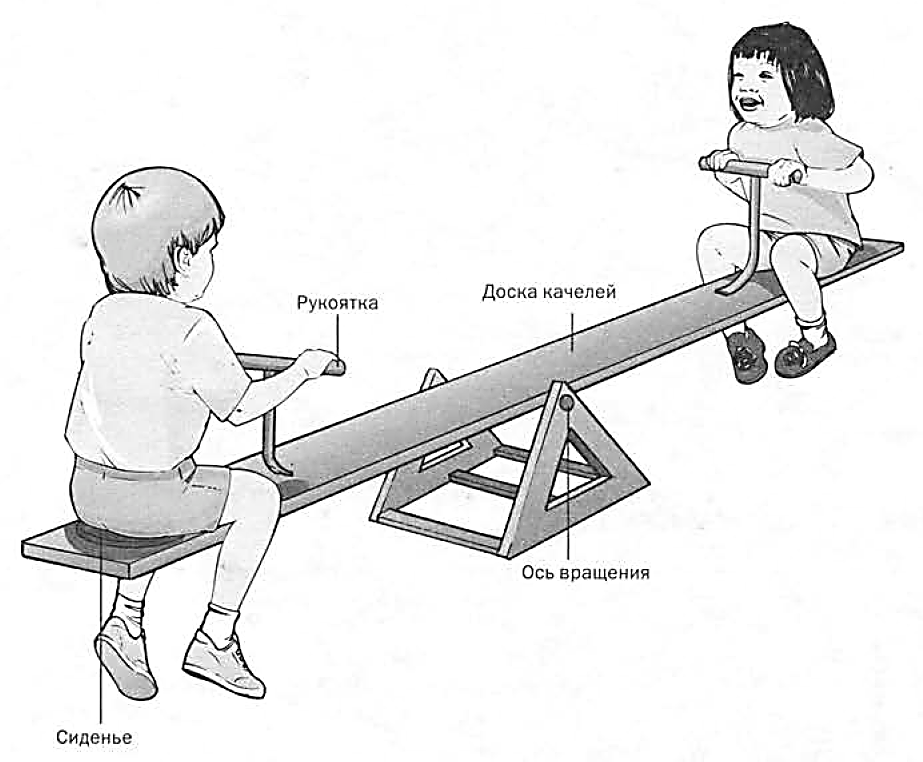
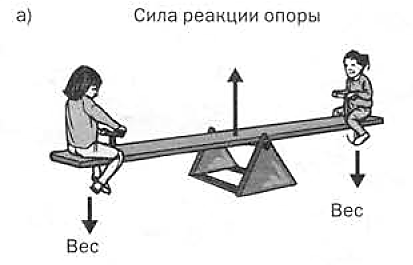
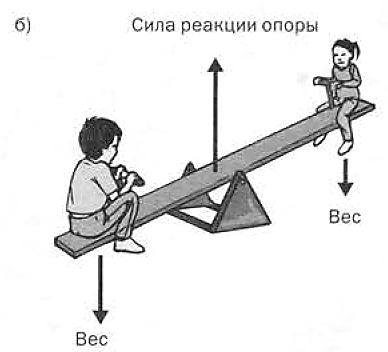
Качели. Любому ребенку, которому приходилось играть на детской площадке с другими детьми, прекрасно известно, что качаться на качелях лучше всего с кем-то, кто весит примерно столько же, сколько ты сам (рис. 2.1.1, а). Партнеры, подходящие друг другу по весу, уравновешивают качели, что позволяет легко раскачиваться. И наоборот, если маленький ребенок качается с большим, то старший рискует больно стукнуться попой, когда его плечо качелей опустится слишком быстро (рис. 2.1.1, б). Зато малыш взлетит вверх, как настоящий астронавт!

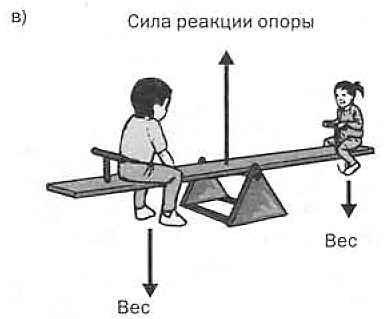
Решить проблему разницы в весе можно разными способами. Например, если напротив большого ребенка на другое плечо качелей усядутся двое маленьких. И любой ребенок прекрасно знает, что если тот, кто потяжелее, сдвинется побли­же к оси вращения (к центру качелей), то качели тоже уравновесятся (рис. 2.1.1, в) и качаться будет столь же удобно, как если бы седоки на обоих концах качелей весили одинаково. Этот весьма полезный прием мы обсудим чуть позже. Но для начала давайте подробнее изучим принципы вращательного движения.

Простоты ради мы не будем учитывать массу и вес самих качелей. В таком случае на качели действуют всего три силы (рис. 2.1.1) — две направленные вниз (вес двух детей) и одна направленная вверх (сила реакции центральной опо­ры). Взглянув на эти три силы, мы сразу же вспоминаем о равнодействующей и ищем некое общее ускорение качелей и "наездников”. Однако мы знаем, что качели всегда остаются на отведенном им месте на детской площадке и вряд ли в ближайшее время вдруг переместятся в захолустье штата Мичиган или к цен­тру Земли. Поскольку неподвижная опора качелей всегда обеспечивает действие силы, направленной вверх и вбок (эта сила необходима для того, чтобы предотвратить возникновение ускорения во всей системе), то приложенная к качелям результирующая сила равна нулю и они не могут оторваться от земли. В общем случае перемещение тела с одного места на другое называется поступательным движением. Качели не участвуют в поступательном движении, но могут пово­рачиваться относительно оси (или точки опоры) и, следовательно, участвуют в другом виде движения. Движение вокруг неподвижной точки (или оси) называ­ется вращательным движением. Пример вращательного движения — движение стрелок часов по циферблату.

Качели интересны именно как пример вращательного движения. Весь их смысл заключается в способности вращаться, благодаря чему один ребенок под­нимается, а другой опускается. Вам может показаться, что подъем и спуск — это не совсем вращение, однако если бы на пути опускающегося плеча качелей не сто­яла земля, то качели совершали бы полный оборот вокруг своей центральной оси. Что же заставляет качели вращаться? И какие выводы мы можем сделать, наблю­дая за их вращением?

Чтобы ответить на эти вопросы, надо изучить кое-какие новые физические величины, связанные с вращением, и рассмотреть законы вращательного движе­ния, которые выражают соотношение этих величин. Мы можем сделать это на примере качелей и других вращающихся объектов, а затем сравним поступатель­ное и вращательное движение.

Представьте себе, что вы придерживаете качели (рис. 2.1.1, а) в горизонталь­ном положении, пока ребенок слева слезает с них. Теперь представьте, что вы их отпустили. Как только вы это сделаете, качели начнут поворачиваться и ребенок справа начнет опускаться. Поначалу качели вращаются медленно, затем быстрее и быстрее, пока бедный малютка с громким стуком не ударится о землю

Если бы нас интересовало только собственно вращение, мы описали бы дви­жение качелей следующим образом:

Сначала качели не вращаются вовсе. Когда мы их отпускаем, они начинают вращаться по часовой стрелке. Скорость вращения качелей по часовой стрел­ке постоянно возрастает до тех пор, пока плечо качелей не ударится о землю.

Это описание сильно напоминает описание полета мяча, упавшего из состояния покоя:

Сначала мяч не движется вовсе. Когда мы его отпускаем, он начинает переме­щаться вниз. Направленная вниз скорость падения мяча постоянно возраста­ет до тех пор, пока он не стукнется о землю.

В эпизоде с качелями описывается вращательное движение, а в эпизоде с мячом — поступательное. Сходство этих явлений — не случайное совпадение; принципы и законы вращательного движения во многом аналогичны принципам и законам движения поступательного. То, что мы уже знаем о поступательном движении, поможет нам разобраться и с вращением.

Движение раскачивающихся качелей. В предыдущей главе мы рассмотрели явление инерции в поступательном дви­жении — движущееся тело стремится продолжить движение, неподвижное тело стремится остаться в покое. Это положение привело нас к первому закону Нью­тона для поступательного движения. Именно для поступательного — это важное уточнение! — потому что теперь мы будем изучать соответствующие положения теории вращательного движения.

Знакомство с новой темой мы начнем с анализа поведения качелей, свобод­ных от внешних воздействий, которые могли бы вызвать вращение. Далее мы по­смотрим, как реагируют качели на внешние воздействия — со стороны собствен­ной оси вращения и со стороны юных пользователей. Поскольку вращательное и поступательное движения имеют много общего, в этой главе проводятся близкие параллели с ранее изученными процессами — катанием на коньках и бросанием мячей.

Предположим, что на детской площадке рядом с вашим домом устанавлива­ют новые качели. Пока что это просто доска, болтающаяся на веревке (рис. 2.1.2). Веревка привязана к середине доски и компенсирует ее вес, но больше никакого воздействия на нее не оказывает. Предположим далее, что доска качелей может вращаться и поворачиваться во все стороны — ничто ее специально не подталки­вает и не крутит — и веревка не мешает ее движению. Итак, подвешенные качели могут повернуться в любом направлении. Вы, наблюдатель, неподвижно стоите рядом и смотрите на качели — как же они себя поведут?

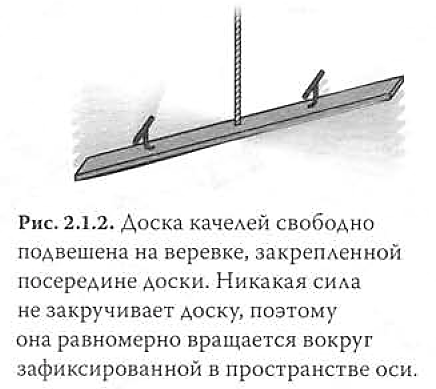
Пока качели неподвижны, они так и останутся неподвижными. Но если они вращаются, то продолжат равномерно вращаться вокруг некой оси в простран­стве. Что заставляет их продолжать вращение? Момент инерции. Вращающееся тело стремится продолжить вращение; если тело не вращается, оно и не стремит­ся вращаться. Так устроена наша Вселенная.

Чтобы точнее описать момент инерции и вращательное движение качелей, необходимо дать определение некоторым физическим величинам, связанным с вращательным движением. Первая из них — угловая координата. В каждый момент времени качели ориентированы определенным образом, то есть имеют определенные угловые координаты. Угловая координата, или угловое перемеще­ние, указывает положение качелей относительно некоего заданного направления; ее можно задать, указав, насколько качели отклонились от начального положения и от оси, вокруг которой они поворачиваются. Угловое перемещение — это вто­ростепенный по значимости вектор, направленный вдоль оси вращения и равный по модулю углу поворота (рис. 2.1.3).

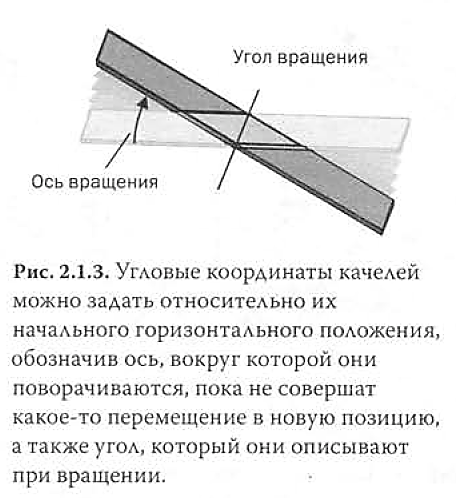
В системе СИ угловые координаты (и угловое перемещение) измеряются в ра­дианах, естественных единицах измерения углов. Эта единица называется есте­ственной, потому что она, в отличие от большинства единиц измерения, выводится непосредственно из геометрии, а не возникла волей какого-то ученого или в ре­зультате какой-то договоренности ученых. Согласно правилам геометрии, длина окружности с радиусом, равным 1, равна 2п. Чтобы выразить угол через дугу этой окружности, мы используем радианы. Например, в полном круге (360') 2п радиан, а прямой угол (90’) равен п/2 радиан. Поскольку радианы — естественные единицы, они часто не указываются при расчетах и определении производных единиц.

Когда качели вращаются, меняется их угловая координата; иначе говоря, они имеют угловую скорость. Угловая скорость — первый важный для нас вектор, ко­торый характеризует вращательное движение и служит мерой быстроты измене­ния угловой координаты; угловая скорость задается модулем (собственно угловой скоростью вращения) и направлением оси, вокруг которой происходит вращение. Угловая скорость качелей — это изменение угла, деленное на время, в течение которого менялся угол.

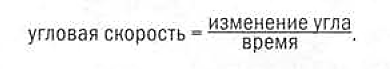
Единица измерения угловой скорости в СИ — радиан в секунду (сокращенно 1/c).

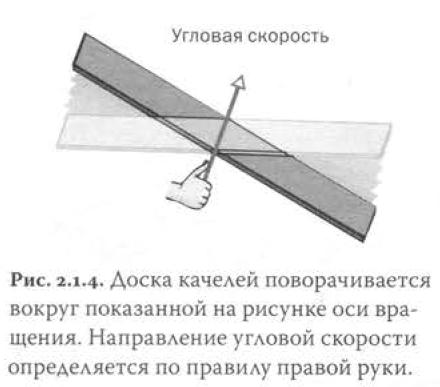
Ось вращения качелей представляет собой линию в пространстве, вокруг ко­торой они поворачиваются. Но одной только этой линии недостаточно — надо еще знать, в какую сторону поворачиваются качели, по часовой стрелке или против.

Чтобы устранить неопределенность, вспомним, что любая прямая имеет два направления. Обозначив прямую, вокруг которой происходит вращение, мы мо­жем посмотреть на плоскость вращения качелей с разных сторон. Глядя с одной стороны, мы увидим, что качели поворачиваются по часовой стрелке; посмотрим с другой стороны — и вращение явно происходит против часовой стрелки. Да­вайте договоримся, что мы смотрим с такой точки зрения, что качели вращаются по часовой стрелке, и что ось вращения направлена от нас к качелям. Такое со­глашение называется правилом правой руки: если обхватить ось вращения пра­вой рукой так, чтобы четыре пальца были направлены в направлении вращения, то отставленный большой палец укажет направление оси вращения (рис. 2.1.4). Можно также назвать это "правилом штопора (буравчика)": когда мы поворачиваем штопор, он врезается в пробку в том направле­нии, в котором надо направить вектор угловой скорости. Когда вы попытаетесь применить правило правой руки на практике, не забудьте переложить эту книгу в левую руку.

У любого преподавателя физики, и я не исключение, непременно находится в группе несколько студентов, которые вос­принимают правило правой руки наоборот. Я никак не мог догадаться, в чем же дело, пока во время одного семинара кто-то не обратил мое внимание на то, что боль­шинство студентов делают записи правой рукой. Чтобы не класть на стол ручку (и по­том снова не брать ее), некоторые из них пытаются проверить правило правой руки с помощью левой — и у них ничего не выхо­дит. Вероятно, они полжизни мучаются, не понимая, почему же у них такая неудобная обувь, — по схожей причине.

Надпись на вывеске: "Товары для левшей".

Отметим, что соблюсти это условие не так важно, как понять, почему при определении вектора угловой скорости необходимо указывать направление вращения. Подобно тому, как вектор скорости поступательного движения характе­ризуется собственно скоростью (модулем) и направлением, в котором происходит поступательное движение, так и угловая скорость имеет численное значение (ско­рость вращения) и направление, в котором происходит вращение.

Теперь мы можем описать вращательное движение висящих на веревке каче­лей. Поскольку на них не действуют внешние силы и они имеют момент инерции, их угловая скорость постоянна. Подвешенные качели постоянно поворачиваются с одной и той же угловой скоростью вокруг одной и той же оси.

Как вы, наверное, догадываетесь, так ведут себя не только качели. Это и есть первый закон Ньютона для вращательного движения: если жесткое тело не раска­чивают и не подвергают внешним воздействиям, оно вращается с постоянной угловой скоростью и совершает одинаковые повороты за равные промежутки времени вокруг фиксированной оси вращения. Под внешними воздействиями здесь подразумеваются моменты силы — так в научном мире называют вращаю­щие (они же крутящие) моменты. Когда вы отвинчиваете крышку банки или запу­скаете волчок, вы прикладываете к ним момент силы.

Этот закон неприменим к качающимся телам и телам изменчивой формы, потому что они участвуют в более сложном движении. Такие тела подчиняются более общему закону — закону сохранения импульса, который мы будем изучать в разделе 2.3.