Индивидуальные индексы
Относительная величина, получаемая при сравнении уровней, называется индивидуальным индексом, если не имеет значения структура изучаемого явления. Индивидуальные индексы обозначаются i. Расчет индивидуальных индексов прост: их определяют вычислением отношения двух индексируемых величин, то есть по формуле (2).
Например, если уровень товарооборота 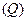 в виде суммы выручки от продажи товара в условиях отчетного периода сравнивается с аналогичным показателем базисного периода, то в итоге получаем индивидуальный индекс выручки (170), показывающий во сколько раз изменилась (или сколько процентов составляет) выручка в отчетном периоде по сравнению с базисным:
в виде суммы выручки от продажи товара в условиях отчетного периода сравнивается с аналогичным показателем базисного периода, то в итоге получаем индивидуальный индекс выручки (170), показывающий во сколько раз изменилась (или сколько процентов составляет) выручка в отчетном периоде по сравнению с базисным:
iQ=Q1/Q0. (170)
Разность между числителем и знаментелем формулы (170) представляет собой абсолютное изменение выручки (171), показывающее на сколько в денежных единицах (например, рублях) изменилась выручка в отчетном периоде по сравнению с базисным:
∆Q = Q1 – Q0. (171)
Аналогично определяются индивидуальные индексы можно для любого интересующего показателя (производительности, заработной платы, себестоимости и т.д.).
В частности, поскольку сумма выручки определяется ценой товара p (от англ. «price») и количеством (физическим объемом, или объемом продаж в натуральном выражении) q (от англ. «quantity») т.е. 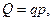 можно определить соответствующие индивидуальные индексы – цены (172) и количества (173):
можно определить соответствующие индивидуальные индексы – цены (172) и количества (173):
ip=p1/p0, (172) iq=q1/q0. (173)
Очевидно, что произведение индивидуальных индексов цены и количества дает индивидуальный индекс выручки (174):
iQ=iqip. (174)
Например, вчера бабушка торговала семечками по 5 руб. за кулёк и всего продала 50 кульков, а сегодня – по 7 руб. и продала 20 кульков. Определим индивидуальный индекс цены по формуле (172): ip = 7/5 = 1,4, то есть бабушка увеличила цену семечек в 1,4 раза, или на 40%. Рассчитаем индивидуальный индекс количества по формуле (173): iq = 20/50 = 0,4, то есть количество проданных семечек сегодня составило 40% от вчерашнего, то есть уменьшилось на 60%. Найдем индивидуальный индекс выручки по формуле (174): iQ = 0,4*1,4 = 0,56, то есть выручка сегодня составила 56% от вчерашней, то есть она уменьшилась на 44%. Рассчитав выручку вчера Q0 = 50*5 = 250 (руб.) и сегодня Q1 = 20*7 = 140 (руб.), можно получить аналогичный результат по формуле (170): iQ = 140/250 = 0,56. Очевидно, что абсолютное изменение выручки по формуле (171) составило: ∆Q = 140 – 250 = –110 (руб.), то есть выручка уменьшилась на 110 руб. (или на 44%), что объясняется изменением количества проданных семечек в 0,4 раза (уменьшением на 60%) и изменением их цены в 1,4 раза (повышением цены на 40%).
Подставим формулу (170) в формулу (174) и выразим выручку отчетного периода:
Q1=iqipQ0. (175)
Формула (175) представляет собой двухфакторную мультипликативную индексную модель итогового показателя, в данном случае – выручки, посредством которой находят изменение этого показателя под влиянием каждого фактора (цены и количества) в отдельности (факторный анализ), то есть:
∆Q = ∆Qq + ∆Qp, (176)
где ∆Qq – изменение выручки под влиянием изменения количества товара q (экстенсивный фактор);
∆Qp – изменение выручки под влиянием изменения цены p товара (интенсивный фактор).
Для проведения факторного анализа по формуле (176) необходимо определить очередность влияния факторов на результативный показатель (выручку), которая может быть следующей:
1) сначала менялось количество q, а затем цена p (то есть количество – это 1-ый фактор, а цена – 2-ой)[54];
2) сначала менялась цена p, а потом количество q (то есть цена – это 1-ый фактор, а количество – 2-ой).
В соответствии с этой очередностью влияния факторов запись факторов в мультипликатиавной модели: то есть формула (175) – это ее запись для количества как 1-го фактора и цены как 2-го. В случае, когда цена является 1-ым фактором, а количество – 2-ым, необходимо мультипликативную модель записывать в виде (177), то есть меняя факторы местами:
Q1=ipiqQ0. (177)
Чтобы найти изменение результативного показателя на основе мультипликативной модели за счет 1-го фактора, необходимо исключить влияние остальных факторов. Тогда при использовании формулы (175) влияние 1-го определяем по формуле (178), а при использовании формулы (177) – по формуле (179):
∆Qq= iqQ0 –Q0 = (iq – 1)Q0, (178) ∆Qp= ipQ0 –Q0 = (ip – 1)Q0. (179)
В нашем примере про бабушку сначала изменилась цена, то есть цена – это 1-ый фактор, а количество – 2-ой, значит необходимо использовать формулу (177) и, как следствие, влияние 1-го фактора – цены определяем по формуле (179): ∆Qp= (1,4–1)*250 = 100 (руб.), то есть повышение цены семечек с 5 до 7 руб. за кулёк должно было увеличить сегодняшнюю выручку на 100 руб., однако выручка уменьшилась на 110 руб., значит – это отрицательное влияние 2-го фактора – изменение количества.
Чтобы найти изменение результативного показателя на основе мультипликативной модели за счет 2-го фактора, необходимо из общего изменения результативного показателя вычесть его изменение под влиянием только 1-го фактора. Тогда, подставляя формулы (171) и (178) в формулу (176), можно выразить влияние второго фактора – цена:
∆Qp = ∆Q – ∆Qq = (Q1 – Q0)– (iqQ0 –Q0) = iqipQ0 – Q0– iqQ0 +Q0 = (iqip – 1 – iq + 1)Q0 = iq (ip–1)Q0.
В итоге получим формулу для расчета влияния второго фактора – цена (180):
∆Qp = iq (ip–1)Q0. (180)
Аналогично, подставляя формулы (171) и (177) в формулу (176) выводится формула для определения влияния второго фактора – количества:
∆Qq = ∆Q – ∆Qp = (Q1 – Q0)– (ipQ0 –Q0) = ipiqQ0 – Q0– ipQ0 +Q0 = (ipiq – 1 – ip + 1)Q0 = ip (iq–1)Q0.
В итоге получим формулу для расчета влияния второго фактора – количества (181):
∆Qq = ip (iq–1)Q0. (181)
В нашем примере про бабушку изменение выручки под влиянием второго фактора – количества определим по формуле (181): ∆Qq = 1,4*(0,4–1)*250 = –210 (руб.), то есть снижение количества проданных семечек с 50 кульков до 20 уменьшило выручку на 210 руб. Проверка правильности расчета влияния факторов осуществляется по формуле (176): ∆Q = 100 + (–210) = –110, что совпадает с общим изменением выручки, рассчитанным ранее по формуле (171).
В статистике нередки случаи использования индексных моделей с тремя и более факторными индексами[55]. В случае необходимости проведения факторного анализа таких моделей применяется метод Чалиева: для определения влияния i-го фактора на результативный показатель необходимо его базисную величину умножить на индексы факторов, влиявших на него с 1-го до i-го фактора и на темп изменения самого i-го фактора. Темп изменения определяется по формуле (80), то есть надо из индекса вычесть единицу (100%).
Например, общая сумма материальных затрат (M) зависит от объема производства продукции (q), от расхода данного материала на единицу продукции – удельного расхода (m) и от цены единицы данного материала (p) т.е. M = qmp. Сравнивая сумму материальных затрат в отчетном периоде с суммой материальных затрат базисного периода получаем (если q - 1-ый фактор, m – 2-ой и p – 3-ий):
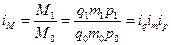 или
или 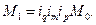 (182)
(182)
Тогда, применяя метод Чалиева, изменение общей суммы материальных затрат ∆M = M1 – M0 объясняется:
1) изменением объема продукции ∆Mq = TqM0 = (iq – 1)M0;
2) изменением удельного расхода материала ∆Mm = iqTmM0 = iq(im – 1)M0;
3) изменением цены на материал ∆Mp = iqimTpM0 = iqim(ip – 1)M0.
Общие индексы
Если изучаемое явление неоднородно и сравнение уровней можно провести только после приведения их к общей мере, экономический анализ выполняют посредством общих индексов. Индекс становится общим, когда в его расчетной формуле показывается неоднородность изучаемой совокупности. Примером неоднородной совокупности является общая масса проданных товаров всех или нескольких видов. Действительно нельзя, например, складывать непосредственно килограммы мяса и рыбы, так как полученный результат в прямом смысле не являлся бы «ни рыбой, ни мясом».
Любые общие индексы могут быть построены 2-мя способами: как агрегатные и как средние из индивидуальных.
Агрегатный индекс является основной и наиболее распространенной формой индекса, если числитель и знаменатель представляют собой набор – «агрегат» (от лат. aggregatus – складываемый, суммируемый) непосредственно несоизмеримых и не поддающихся суммированию элементов – сумму произведений двух величин, одна из которых меняется (индексируется), а другая остается неизменной в числителе и знаменателе (вес индекса). Вес индекса служит для целей соизмерения индексируемых величин.
Например, общую сумму выручки можно записать в виде агрегата (суммы произведений объемного показателя q на взвешивающий – p), т.е.
∑Q = ∑qp. (183)
Отношение агрегатов, построенных для разных условий, дает общий индекс показателя в агрегатной форме. Так получают индекс общего объема товарооборота (выручки), показывающий во сколько раз он изменился (или сколько процентов составляет) в отчетном периоде по сравнению с базисным:
IQ= 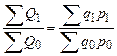 .(184)
.(184)
Разность между числителем и знаментелем формулы (184) представляет собой абсолютное изменение общего товарооборота (выручки) (185), показывающее на сколько в денежных единицах (например, рублях) он изменился в отчетном периоде по сравнению с базисным:
∆∑Q = ∑Q1 – ∑Q0 = ∑q1p1 – ∑q0p0. (185)
Например, дедушка торговал яблоками двух сортов: «антоновкой» и «белым наливом», результаты торговли за 2 дня представлены в таблице 51:
Таблица 51. Условные данные о торговле яблоками дедушкой за 2 дня
| Сорт яблок | Цена за кг, руб. | Объем продаж, кг | ||
| вчера (p0) | сегодня (p1) | вчера (q0) | сегодня (q1) | |
| Антоновка | ||||
| Белый налив |
Рассчитаем выручку дедушки по формуле (183):
– в отчетном периоде: ∑Q1= 18*160+25*120 = 5880 (руб.) – это выручка от продажи яблок сегодня;
– в базисном периоде: ∑Q0= 20*100+22*150 = 5300 (руб.) – это выручка от продажи яблок вчера.
Теперь определим изменение общей выручки дедушки:
– по формуле (184): IQ=5880/5300 = 1,1094, то есть выручка увеличилась в 1,1094 раза, или на 10,94%.
– по формуле (185): ∆∑Q =5880 – 5300 = 580, то есть выручка увеличилась на 580 руб.
При анализе изменения общего объема товарооборота (выручки) это изменение также объясняется изменением уровня цен и количества проданных товаров. Влияние этих факторов выражается агрегатными индексами физического объема (количества) и цен.
Если уровни взвешивающего показателя взяты по данным базисного периода, то получают агрегатный индекс Ласпейреса:
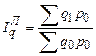 ; (186)
; (186) 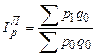 . (187)
. (187)
Формула (186) применяется, когда количество – это 1-ый фактор, а формула (187) – когда цена является 1-ым фактором.
Если уровни взвешивающего показателя взяты по данным отчетного периода, то получают агрегатный индекс Пааше:
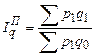 ; (188)
; (188) 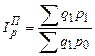 . (189)
. (189)
Формула (188) применяется, когда количество – это 2-ой фактор, а формула (189) – когда цена является 2-ым фактором.
Произведение агрегатных индексов Ласпейреса и Пааше дает общий индекс выручки:
IQ = 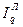
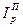 ;(190) IQ =
;(190) IQ = 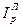
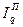 . (191)
. (191)
Для облегчения запоминания студентами формул Ласпейреса и Пааше предлагаю обратить внимание на букву «Ш» в слове «Пааше», которая напоминает «111» - так обозначены отчетные периоды в общей формуле (две единицы – в числителе и одна – в знаменателе). В формуле Ласпейреса нет буквы «Ш», значит в ней не будет трех единиц, а будут три нуля (два нуля – в знаменателе и один – в числителе).
В нашем примере про дедушку (как и в примере про бабушку) цена яблок – это 1-ый фактор, а количество – 2-ой. Поэтому для определения агрегатного индекса цен применяем формулу (187):
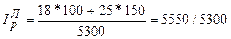 = 1,0472, то есть цена на яблоки увеличилась в 1,0472 раза (на 4,72%).
= 1,0472, то есть цена на яблоки увеличилась в 1,0472 раза (на 4,72%).
Определим агрегатный индекс количества проданных яблок по формуле (188):
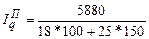 = 1,0594, то есть количество проданных яблок выросло в 1,0594 раза (на 5,94%).
= 1,0594, то есть количество проданных яблок выросло в 1,0594 раза (на 5,94%).
Контроль правильности расчетов производим по формуле (191): IQ= 1,0472*1,0594 = 1,1094, то есть изменение общей выручки дедушки в 1,1094 раза (на 10,94%) объясняется изменением цены в 1,0472 раза (на 4,72%) и изменением количества продаж в 1,0594 раза (на 5,94%).
Из формул (186) – (189) видно, что индексы Ласпейреса и Пааше по одному и тому же фактору не равны между собой, то есть 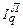 ≠
≠ 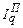 и
и 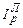 ≠
≠ 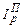 . Американский экономист Гершенкрон обширными расчетами установил, что по одному и тому же фактору индекс Ласпейреса обычно больше индекса Пааше, и это открытие названо эффектом Гершенкрона[56], то есть
. Американский экономист Гершенкрон обширными расчетами установил, что по одному и тому же фактору индекс Ласпейреса обычно больше индекса Пааше, и это открытие названо эффектом Гершенкрона[56], то есть 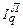 >
> 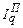 и
и 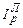 >
> 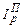 .
.
Когда нет возможности определить очередность влияния факторов на результативный показатель (какой из факторов 1-ый – цена или количество) проблематично выбрать одну из формул (186) или (187) и (188) или (189). В таких случаях рекомендуется применить все формулы (186) – (189) и рассчитать среднюю геометрическую величину из однофакторных индексов – индексы Фишера:
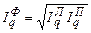 ; (192)
; (192) 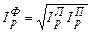 . (193)
. (193)
Сравнивая значения индексов Фишера, которые показывают среднее изменение цен (193) и количества (192), решается вопрос об очередности влияния факторов: какой из индексов показывает большее изменение, тот фактор и считают 1-ым.
Из формул (190) и (191) легко получить двухфакторные мультипликативные индексные модели общей выручки, подставив в них формулу (184) и выразив ∑Q1:
∑Q1= 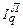
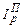 Q0, (194)∑Q1=
Q0, (194)∑Q1= 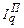
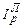 Q0. (195)
Q0. (195)
Формула (194) применяется, когда количество товара – 1-ый фактор, а цена 2-ой, а формула (195) – наоборот, цена – 1-ый фактор, а количество – 2-ой. Тогда, применяя метод Чалиева, можно выполнить факторный анализ, то есть объяснить изменение результативного показателя (общей выручки) изменением каждого фактора (цен и количества) в отдельности в абсолютных (денежных) единицах. Более детальный анализ изменения итогового показателя возможен при изучении так называемых структурных сдвигов.
В нашем примере про дедушку мы применяли формулу (187), значит должны производить факторный анализ по модели (195). Тогда, применяя метод Чалиева, изменение общей выручки ∆∑Q = ∑Q1 – ∑Q0 объясняется изменением:
1) количества проданных проданных яблок ∆∑Qq = ( 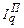 –1) ∑Q0 =(1,0594–1)*5300 ≈ 315 (руб.)
–1) ∑Q0 =(1,0594–1)*5300 ≈ 315 (руб.)
2) цены яблок ∆∑Qp = 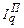 (
( 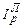 –1) ∑Q0 =1,0594*(1,0472–1)*5300 ≈ 265 (руб.)
–1) ∑Q0 =1,0594*(1,0472–1)*5300 ≈ 265 (руб.)
Проверка правильности расчета влияния факторов: ∆∑Q = 265 + 315 = 580, что совпадает с общим изменением общей выручки, рассчитанным ранее по формуле(185).
Помимо записи общих индексов в агрегатной форме на практике часто используют формулы их расчета как величин, средних из соответствующих индивидуальных индексов. Так, общий индекс выручки может быть записан как средняя арифметическая взвешенная (196) или средняя гармоническая взвешенная (197) из индивидуальных индексов выручки по отдельным товарным группам:
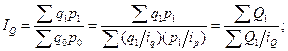 (196)
(196) 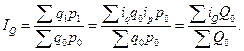 (197)
(197)
В формуле (196) весами являются показатели объема товарооборота отдельных товарных групп в отчетном периоде, в формуле (197) – в базисном.
Аналогично через индивидуальных индексы количества товара и цены могут быть выражены общие агрегатные индексы Ласпейреса и Пааше:
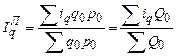 ; (198)
; (198) 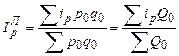 ; (199)
; (199)
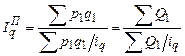 ; (200)
; (200) 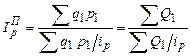 . (201)
. (201)
Дата добавления: 2017-09-19; просмотров: 559;
