Координатный способ задания движения точки
Движение точки в декартовых координатах считается заданным, если известны координаты точки как непрерывные, дважды дифференцируемые функции времени (рис. 24), т. е. заданы уравнения движения точки в декартовых координатах:
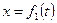 ,
, 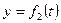 ,
, 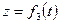 . (50)
. (50)
Уравнения движения точки в декартовых координатах полностью определяют движение точки. Они позволяют найти положение точки, ее скорость и ускорение в любой момент времени.
Разложим радиус-вектор и скорость точки на составляющие, параллельные осям координат. Получим
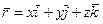 ,
, 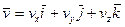 , (51)
, (51)
где 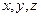 – координаты точки
– координаты точки 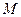 ;
; 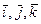 – единичные векторы осей координат;
– единичные векторы осей координат; 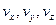 – проекции скорости на оси координат.
– проекции скорости на оси координат.
Учитывая (51), согласно определению скорости, имеем:
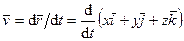
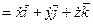 , (52)
, (52)
Сравнивая (52) и (51), получаем для проекций скорости на декартовы оси координат следующие формулы:
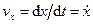 ,
, 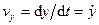 ,
, 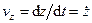 . (53)
. (53)
Проекция скорости точки на какую-либо координатную ось равна первой производной по времени от соответствующей координаты этой точки. По проекциям определяют числовое значение (модуль) скорости и косинусы углов вектора скорости с осями координат:
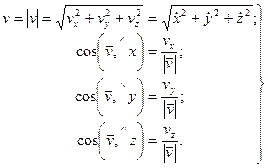 (54)
(54)
Разложим ускорение точки на составляющие, параллельные осям декартовой системы координат. Получим
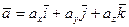 , (55)
, (55)
где 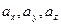 – проекции ускорения на координатные оси. Согласно определению ускорения и формулам (52) и (51), имеем
– проекции ускорения на координатные оси. Согласно определению ускорения и формулам (52) и (51), имеем
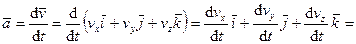
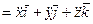 . (56)
. (56)
Формулы для проекций ускорения на оси декартовой системы координат:
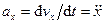 ,
, 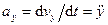 ,
, 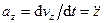 . (57)
. (57)
Проекция ускорения на какую-либо координатную ось равна второй производной по времени от соответствующей координаты движущейся точки.
Числовое значение ускорения и косинусы углов вектора ускорения с осями координат определяем по формулам
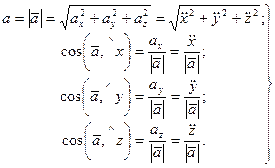 . (58)
. (58)
Касательная и нормальная составляющие ускорения вычисляются по формулам:
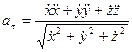 ,
, 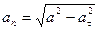 . (59)
. (59)
При 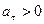 движение точки ускоренное, при
движение точки ускоренное, при 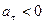 – замедленное.
– замедленное.
Дата добавления: 2017-09-19; просмотров: 847;
