Решение задач статики
Пример 1.На угольник  (
( 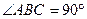 ), конец
), конец  которого жестко заделан, в точке
которого жестко заделан, в точке  опирается стержень
опирается стержень 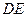 (рис. 19,а). Стержень имеет в точке
(рис. 19,а). Стержень имеет в точке 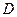 неподвижную шарнирную опору и к нему приложена сила
неподвижную шарнирную опору и к нему приложена сила 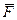 , а к угольнику – равномерно распределенная на участке
, а к угольнику – равномерно распределенная на участке 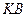 нагрузка интенсивности
нагрузка интенсивности 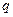 и пара с моментом
и пара с моментом 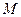 .
.
Дано: 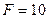 кН,
кН, 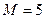
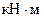 ,
, 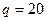
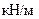 ,
, 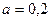 м.
м.
Определить: реакции в точках 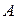 ,
, 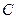 ,
, 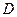 .
.
Решение:
1. Для определения реакций расчленим систему и рассмотрим сначала равновесие стержня 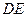 (рис. 19,б). Проведем координатные оси
(рис. 19,б). Проведем координатные оси 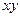 и изобразим действующие на стержень силы: силу
и изобразим действующие на стержень силы: силу 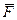 , реакцию
, реакцию 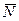 , направленную перпендикулярно стержню, и составляющие
, направленную перпендикулярно стержню, и составляющие 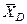 и
и 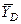 реакции шарнира
реакции шарнира 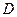 . Для полученной плоской системы сил составляем три уравнения равновесия:
. Для полученной плоской системы сил составляем три уравнения равновесия:
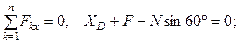 (32)
(32)
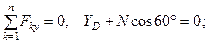 (33)
(33)
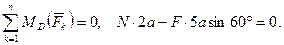 (34)
(34)
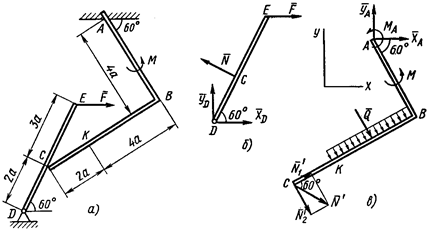
Рис. 19
2. Теперь рассмотрим равновесие угольника (рис. 19,в). На него действуют сила давления стержня 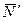 , направленная противоположно реакции
, направленная противоположно реакции 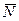 , равномерно распределенная нагрузка, которую заменяем силой
, равномерно распределенная нагрузка, которую заменяем силой 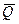 , приложенной в середине участка
, приложенной в середине участка 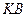 (численно
(численно 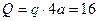 кН), пара сил с моментом
кН), пара сил с моментом 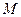 и реакция жесткой заделки, слагающаяся из силы, которую представим составляющими
и реакция жесткой заделки, слагающаяся из силы, которую представим составляющими 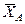 и
и 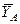 , и пары с моментом
, и пары с моментом 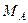 . Для этой плоской системы сил тоже составляем три уравнения равновесия:
. Для этой плоской системы сил тоже составляем три уравнения равновесия:
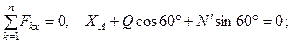 (35)
(35)
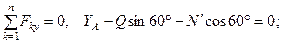 (36)
(36)
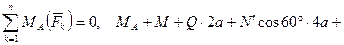
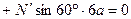 . (37)
. (37)
При вычислении момента силы 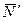 разлагаем ее на составляющие
разлагаем ее на составляющие 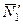 и
и 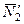 и применяем теорему Вариньона. Подставив в составленные уравнения числовые значения заданных величин и решив систему уравнений (32)–(37), найдем искомые реакции. При решении учитываем, что численно
и применяем теорему Вариньона. Подставив в составленные уравнения числовые значения заданных величин и решив систему уравнений (32)–(37), найдем искомые реакции. При решении учитываем, что численно 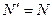 в силу равенства действия и противодействия.
в силу равенства действия и противодействия.
Ответ: 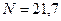 кН,
кН, 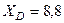 кН,
кН, 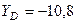 кН,
кН, 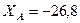 кН,
кН, 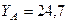 кН,
кН, 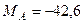
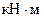 . Знаки минус указывают, что силы
. Знаки минус указывают, что силы 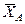 ,
, 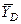 и момент
и момент 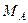 направлены противоположно показанным на рис. 19.
направлены противоположно показанным на рис. 19.
Пример 2.Горизонтальная прямоугольная плита весом 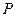 (рис. 20) закреплена сферическим шарниром в точке
(рис. 20) закреплена сферическим шарниром в точке 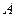 , цилиндрическим (подшипником) в точке
, цилиндрическим (подшипником) в точке 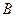 и невесомым стержнем
и невесомым стержнем 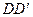 . На плиту в плоскости, параллельной
. На плиту в плоскости, параллельной 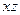 , действует сила
, действует сила 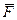 , а в плоскости, параллельной
, а в плоскости, параллельной 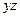 , – пара сил с моментом
, – пара сил с моментом 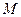 .
.
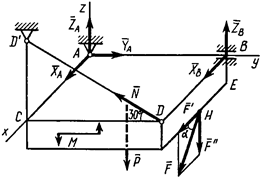 Дано:
Дано: 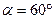 ,
, 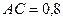 м,
м, 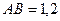 м,
м, 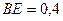 м,
м, 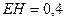 м,
м, 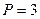 кН,
кН, 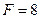 кН,
кН, 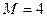
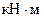 .
.
Определить: реакции опор 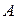 ,
, 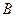 и стержня
и стержня 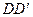 .
.
 Решение:
Решение:
1. Рассмотрим равновесие плиты. На плиту действуют заданные силы 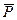 ,
, 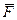 и пара с моментом
и пара с моментом 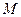 , а также реакции связей. Реакцию сферического шарнира разложим на три составляющие
, а также реакции связей. Реакцию сферического шарнира разложим на три составляющие 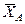 ,
, 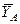 и
и 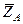 , цилиндрического (подшипника) – на две составляющие
, цилиндрического (подшипника) – на две составляющие 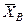 и
и 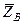 (в плоскости, перпендикулярной оси подшипника); реакцию
(в плоскости, перпендикулярной оси подшипника); реакцию 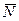 стержня направляем вдоль стержня от
стержня направляем вдоль стержня от 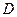 к
к 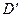 , предполагая, что он растянут.
, предполагая, что он растянут.
2. Для определения шести неизвестных реакций составляем шесть уравнений равновесия действующей на плиту пространственной системы сил:
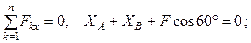 (38)
(38)
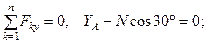 (39)
(39)
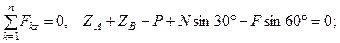 (40)
(40)
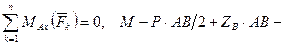
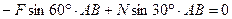 ; (41)
; (41)
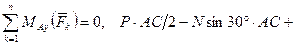
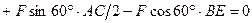 ; (42)
; (42)
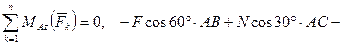
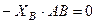 . (43)
. (43)
Для определения моментов силы 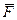 относительно осей
относительно осей 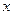 и
и 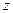 разлагаем ее на составляющие
разлагаем ее на составляющие 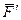 и
и 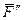 , параллельные осям
, параллельные осям 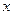 и
и 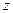 (
( 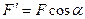 ,
, 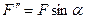 ), и применяем теорему Вариньона.
), и применяем теорему Вариньона.
Аналогично можно поступить при определении моментов реакции 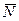 .
.
Подставив в составленные уравнения числовые значения всех заданных величин и решив эти уравнения, найдем искомые реакции.
Ответ: 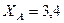 кН,
кН, 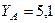 кН,
кН, 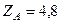 кН,
кН, 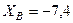 кН,
кН, 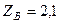 кН,
кН, 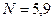 кН. Знак минус указывает, что реакция
кН. Знак минус указывает, что реакция 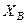 направлена противоположно показанной на рис. 20.
направлена противоположно показанной на рис. 20.
ЛЕКЦИЯ № 3
КИНЕМАТИКА
Кинематика точки
В кинематике точки рассматриваются характеристики движения точки, такие, как скорость, ускорение, и методы их определения при различных способах задания движения. Важным в кинематике точки является понятие траектории. Траекторией точки называется геометрическое место ее последовательных положений в пространстве с течением времени относительно рассматриваемой системы отсчета. По виду траекторий движения точки делятся на прямолинейные и криволинейные.
Задать движение точки – значит задать правило, с помощью которого можно указать положение точки в любой момент времени. Существуют векторный, координатный и естественный способы задания движения точки.
Дата добавления: 2017-09-19; просмотров: 547;
