ТРЕТИЙ ЗАКОН ТЕРМОДИНАМИКИ. ТЕПЛОВАЯ ТЕОРИЯ НЕРНСТА

Ранее нами были рассмотрены способы определения внутренней энергии и энтальпии, а также расчеты энергий Гиббса и Гельмгольца. Теперь остановимся на возможности расчета энтропии. Подобная возможность возникает после ознакомления с третьим законом термодинамики. Его следует рассматривать в качестве постулата о предельном значении энтропии и ее изменениях в процессах, происходящих вблизи абсолютного нуля температуры.

Существует несколько формулировок III закона термодинамики:

1. Постулат Планка

Энтропия любого термодинамически равновесного процесса при абсолютном нуле температуры равна нулю;

2. Абсолютный нуль температур не достижим (принцип недостижимости нуля температуры);

3. По мере приблежения к абсолютному нулю значения энтальпии ∆H и энергия ∆G сближаются (тепловая теорема Нернста).

ТЕПЛОВАЯ ТЕОРЕМА НЕРНСТА

Уравнение Гиббса-Гельмгольца:

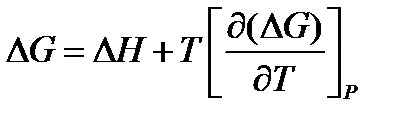
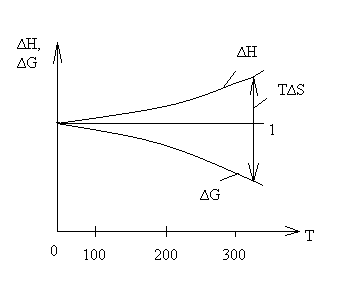
Тепловая теорема Нернста показывает, что по мере приближения к абсолютному нулю происходит сближение между энтальпией ∆Н и энергией Гиббса ∆G, а при абсолютном нуле сближаются кривые, характеризующие изменение ∆Н и ∆G от температуры, и образующаяся общая касательная 1 параллельна оси температуры.

При Т → 0:

1. ∆G =∆H;

2. ∆G =∆H=0;

3.

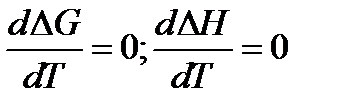
1- Общая касательная

Теорема Нернста: Вблизи абсолютного нуля первая производная по температуре энергии Гиббса равна первой производной изменения энтальпии и равна нулю.

Следствие:

1. ;

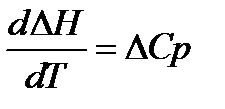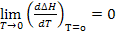
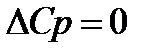
Теплоёмкость вещества при абсолютном нуле температуры равна нулю.

2. ;

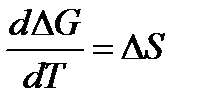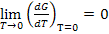
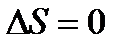
Изменение энтропии при абсолютном нуле температуры равно нулю.

При этом наблюдется так называемое явление «вырождение», когда по мере приближения к абсолютному нулю свойства тел все меньше зависят от температуры.

Обратимся к формуле 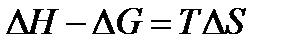, т.е. в соответствии с тепловой теоремой Нернста разность между кривыми ∆Н и ∆G есть Т∆S. При этом Т → 0 изменение энтропии, согласно 2 следствию теоремы Нернста, становится близким к нулю, и кривые начинают сходиться.

Расширенная формулировка Планка

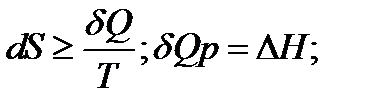
При изменение температуры от Т₁ до Т₂ изменение энтропии можно выразить следующим образом:

;

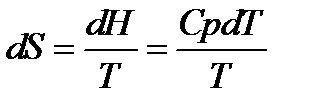
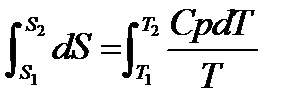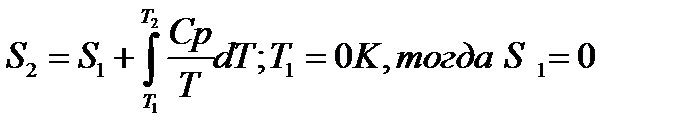
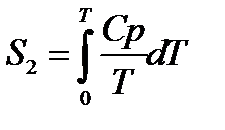
При помощи этого уравнения можно получить абсолютное значение энтропии вещества. Отметим существенное отличие абсолютных значений энтропии от значения других характеристических функций (∆U,∆H,∆G и ∆F), которые являются разностью двух состояний, а не абсолютными значениями.

При абсолютном нуле способность системы к рассеянию энергии иссекает; например, у совершенного

кристалла при абсолютном нуле все атомы находятся в регулярном однородном состояние без разупорядогенности. Они фиксированы в узлах кристаллической решетки и лишены возможности совершать какое - либо движение.

1. Первая строгая формулировка Планка:

Энтропия правильно образованного кристалла при Т=0К равна 0.

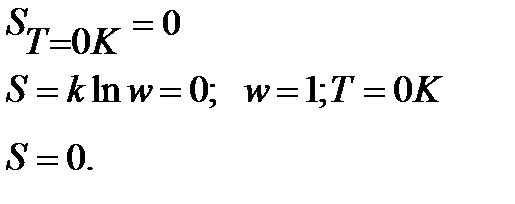
Подчеркнем, что речь идет о правильно образованном, бездефектном, совершенном кристалле. Большинство реальных кристаллов содержат примеси, имеют дефекты, а их энтропия даже при абсолютном нуле несколько больше нуля.

2. Можно показать, что энтропия равна:

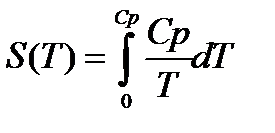
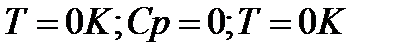
По мере приближения к абсолютному нулю, когда Т→0 , теплоёмкость становиться бесконечно малой величиной и стремится к нулю. Тогда подынтегральное выражение в правой части управления (1) в результате деления двух бесконечно малых величин становится неопределённым, а само уравнение теряет смысл. Из этого в свою очередь вытекает следствие о недостижимости абсолютного нуля температуры. У каждого тела существует своя критическая температура , ниже которой охладить тело невозможно.

РАСЧЕТ АБСОЛЮТНОГО ЗНАЧЕНИЯ ЭНТРОПИИ

Третий закон термодинамики используется для вычисления абсолютных энтропий простых и сложных веществ. Абсолютной энтропией называется энтропия, отсчитанная относительно абсолютного нуля температуры S(0)=0.

Для расчетов необходимо учитывать следующие уравнения.

1.

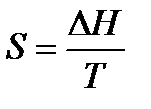
2.

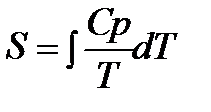
3.

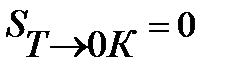
Если вещество может находиться в различных агрегатных состояниях, то следует учитывать изменение энтропии при фазовых переходах. Тогда в общем случае для вещества в газообразном состоянии абсолютная энтропия будет складываться из следующих составляющих:

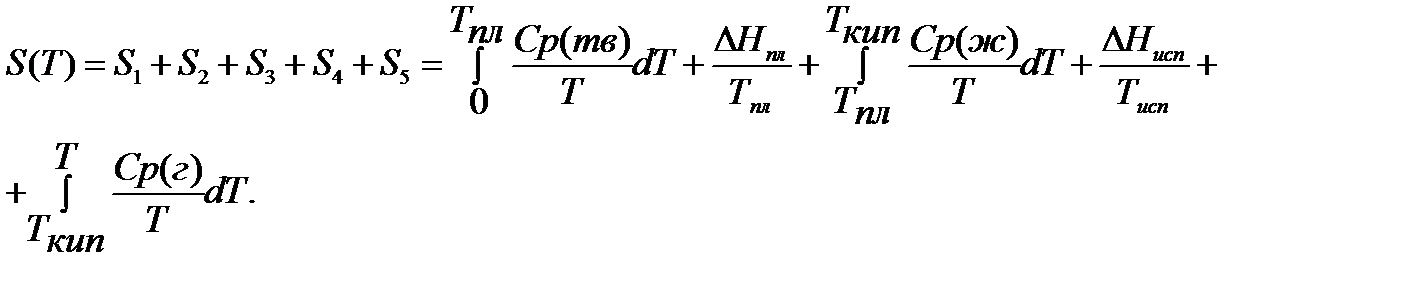
По этому уравнению можно вычислить абсолютные энтропии веществ в твердом, жидком и газообразном состояниях.

Пример. Рассчитать энтропию воды при t=150⁰C.

Энтропия воды при t=150⁰C(423К) равна: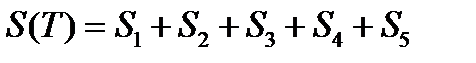

;

;

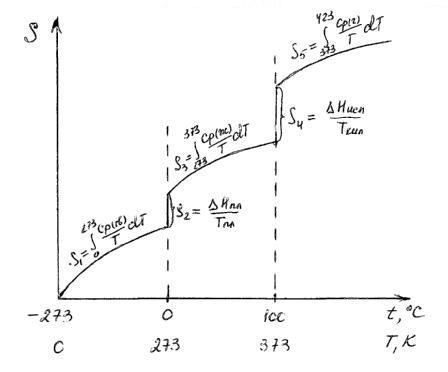
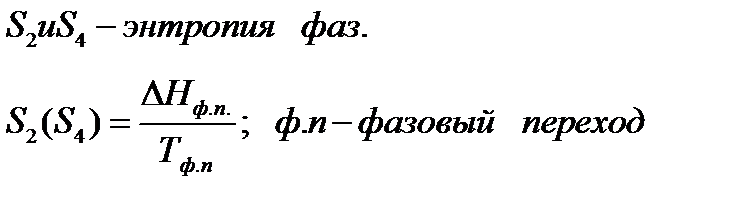
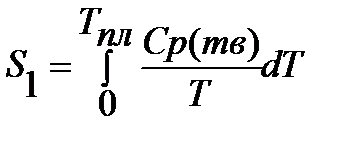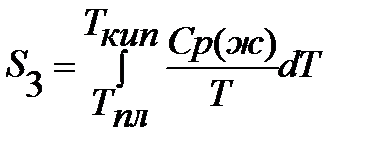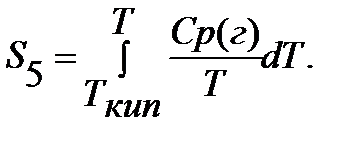
Третий закон термодинамики можно использовать для расчета химических равновесий.

РАСЧЕТ КОНСТАНТЫ РАВНОВЕСИЯ К_Р:

I. По табличным значениям.

II. Интегрирование изобары Вант-Гоффа.

III. Метод комбинированных равновесий.