Усеченные законы распределения
Пусть случайная величина Химеет функцию распределения F(x), заданную на всей числовой оси. Выберем на этой оси интересующий нас отрезок [a,b] (может быть a = - ∞, b = + ∞).Распределение случайной величины Х со значениями, принадлежащими только рассматриваемому отрезку, называется усеченным.
Функция распределения усеченного закона выражается через исходную функцию распределения соотношением:
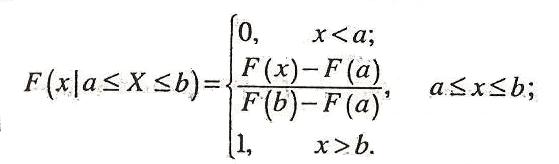
Функция плотности усеченного распределения выражается через исходную соотношением:
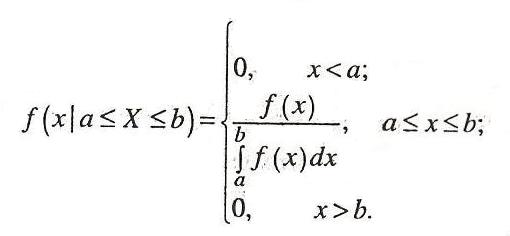
Для дискретных случайных величин интеграл можно заменить соответствующей суммой.
Пример.Среднее время обслуживания покупателя продавцом составляет четыре минуты и подчинено показательному распределению. Продавец уже потратил четыре минуты на обслуживание очередного покупателя. Найти вероятность того, что он затратит еще не менее двух минут на обслуживание этого покупателя.
Решение. Имеем закон распределения времени Т обслуживания очередного покупателя в виде
f(t) = λe -λt , где λ = ¼.
С учетом того фактора, что Т>4,имеем усеченное показательное распределение в виде f(t) = Сλe –λt,t>4.
Параметр Сопределяется из соотношения

Находим С = е.
Получаем усеченное распределение вида
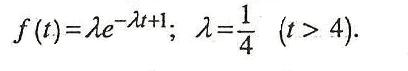
Тогда искомая вероятность равна
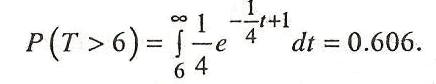
Дата добавления: 2017-09-19; просмотров: 234;
