Основные сведения о программе 3 страница
User Definitions — открытие и просмотр глобальных определений пользователя, сделанных с помощью директивы .Define/
Model Parameters Limits Editor— открытие окна редактирования ограничений на параметры моделей.
Components Palettes — включение различных наборов компонентов. Удобно для рисования схем различного назначения. Самые употребительные наборы — Analog и Digital.
A N A L Y S I S :
Содержит команды запуска различных режимов моделирования:
Transient... (Alt+1) — анализ переходных процессов.
AC... (Alt+2) — анализ частотных характеристик
DC ... (Alt+3) — Анализ передаточных функций по постоянному току
Dynamic DC (Alt+4) — Расчет режима по постоянному току и его динамическое отображение на схеме
Transfer Function... (Alt+5) — Расчет передаточных функций по постоянному току, а также входного и выходного сопротивления
Sensitivity... (Alt+6) — Расчет чувствительностей по постоянному току одного или нескольких выражений по отношению к одному или нескольким параметрам
Probe Transient... (Ctrl+Alt+1) — анализ переходных процессов и отображение их результатов в режиме Probe.
Probe AC... (Ctrl+Alt+2) — анализ частотных характеристик и отображение их результатов в режиме Probe.
Probe DC... (Ctrl+Alt+3) — анализ передаточных функций по постоянному току и отображение их результатов в режиме Probe.
Следует отметить, что при запуске любого режима Probe (Transient, AC, DC) в верхней части экрана появляются новые пункты меню: Probe, Vertical, Horizontal, которые содержат команды управления этим режимом (они будут рассмотрены ниже).
2. Форматы задания компонентов
2.1. Общие сведения
Параметры всех электронных компонентов задаются при помещении компонента в принципиальную схему — щелчком левой клавиши мыши открывается окно задания параметров соответствующего пассивного (активного) компонента.
Все компоненты в MicroСAP-7 могут быть заданы двумя способами:
· непосредственным заданием в открывшемся окне параметров номинального значения компонента (позиция VALUE) или (и) имени используемой модели (позиция MODEL);
· заданием в окне параметров компонента в строке VALUE имени переменной, обозначающей номинал компонента (например Rload, Cout, Cin, Lpins и т.д.) и последующим текстовым вводом информации, ставящим в соответствие этой переменной его номинал или модель. Текстовый ввод информации выполняется директивой «.Define» и может быть осуществлен как в схемном окне (что более наглядно), так и в текстовом.
Задание вторым способом является более универсальным. Оно предоставляет пользователю ряд дополнительных возможностей при выполнении анализа, с которыми читатель познакомится в последующих примерах.
Ввод номинальных значений компонентов осуществляется в системе СИ, за исключением катушки с магнитным (нелинейным) сердечником. Значения компонентов задаются либо непосредственно (2600), либо в показательной форме (2.3E3), либо условными буквенными обозначениями (5K). Используются следующие буквенные обозначения для множителей (см. табл. 2.1):
Таблица 2.1. Буквенные обозначения множителей для численных значений
| 10-15 | 10-12 | 10-9 | 10-6 | 10-3 | 103 | 106 | 109 | 1012 |
| фемто | пико | нано | микро | милли | кило | мега | гига | тера |
| F (f) | P (p) | N (n) | U (u) | M (m) | K (k) | MEG (meg) | G (g) | T (t) |
На рис. 2.1. приведен пример задания одного из пассивных компонентов — резистора. В рассмотренном примере на экране отображается позиционное обозначение компонента (PART), величина (VALUE) и имя модели, что определяется установкой соответствующих флажков отображения в окне задания компонента (в данном случае Resistor). Отметим, что величина любого пассивного компонента (сопротивление резистора, емкость конденсатора, индуктивность катушки) может определяться как любая функция узловых напряжений схемы, токов ветвей, времени и температуры, что выгодно отличает программу MicroCap-7 от PSPICE.
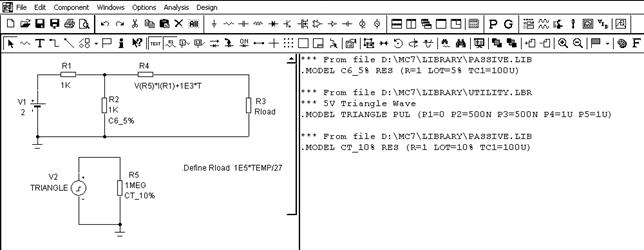
Рис. 2.1 Способы задания компонента
При создании принципиальных схем используются числа, переменные и математические выражения следующего вида.
2.1.1. Числа
Числовые значения параметров компонентов представляются в виде:
· действительных чисел с фиксированным десятичным знаком (обратим внимание, что в качестве десятичного знака в программе МС7 используется точка). Например, сопротивление 2,5 кОм, записывается как 2500 или 2.5k, а емкость 1 мкФ как 0.000001;
· действительных чисел с плавающей точкой, например, емкость 1.5 мкФ может быть записана как 1.5Е-6;
· действительных чисел с плавающей точкой в инженерной интерпретации, согласно которой различные степени десяти обозначаются буквами (см. табл. 2.1).
Для экономии места на осях X, Y графиков результатов моделирования малая буква "m" обозначает 103, большая буква "М" — 106 (вместо MEGA). Во всех остальных случаях большие и малые буквы не различаются.
Например, сопротивление 1,5 МОм может быть записано как 1.5MEG, 1.5meg или 1500К, емкость 1 мкФ как 1U или 1uF. В последнем примере показано, что для большей наглядности после стандартных буквенных обозначений допускается помещать любые символы, которые при интерпретации чисел не будут приниматься во внимание. Пробелы между числом и буквенным суффиксом не допускаются!
2.1.2. Переменные
В программе МС7 ряд констант и переменных имеют стандартные значения:
Т— время в секундах;
F — частота в герцах;
Е — ЕХР(1)=2,718281828;
S — комплексная переменная, используемая при анализе аналоговых устройств (в курсе ОТЦ и Мат. Анализа она обозначалась p);
GMIN — минимальная проводимость ветви, задаваемая в диалоговом окне Options>Global settings;
PI — число p=3.14159265389795;
TEMP — температура компонентов в градусах Цельсия;
VT — температурный потенциал р-п—перехода, равный 1,3806226×10–23х (273,15+ТЕМР)/(1,6021918×1019); при ТЕМР=27°С VT=25,86419mB;
J — корень квадратный из –1;
Tmin — начальный момент времени расчета переходных процессов;
Тmах — конечный момент времени расчета переходных процессов;
Fmin — начальная частота расчета частотных характеристик;
Fmax — конечная частота расчета частотных характеристик;
PGT — общая мощность, генерируемая в схеме;
PST— общая мощность, запасаемая в схеме;
РОТ — общая рассеиваемая в схеме мощность;
Z — комплексная переменная, используемая при анализе дискретных устройств (цифровых фильтров).
Номера узлов, присваиваемые программой МС7 автоматически, представляют собой целые числа, например 0, 2, 25. Кроме того, пользователь по команде Options>Mode/Textможет присвоить любому узлу имя в виде текстовой алфавитно-цифровой переменной, начинающейся с буквы или символа "_" и содержащей не более 50 символов, например А1, Out, Reset.
В математических выражениях могут использоваться следующие переменные (см. табл. 2.2):
Таблица 2.2. Переменные, используемые в программе Microcap-7
| D(A) | Логическое состояние цифрового узла А |
| V(A) | Напряжения на узле А (напряжения измеряются относительно узла "земли", которой программа присваивает номер 0) |
| V(A,B) | Разность потенциалов между узлами А и В |
| V(D1) | Напряжение между выводами двухвыводного компонента D1 |
| I(D1) | Ток через двухвыводной компонент D1 |
| I(A,B) | Ток через ветвь между узлами А и В (между этими узлами должна быть включена единственная ветвь) |
| IR(Q1) | Ток, втекающий в вывод R компонента Q1 с количеством выводов больше 2 |
| VRS(Q1) | Напряжение между выводами R и S компонента Q1 с количеством выводов больше 2 |
| CRS(Q1) | Емкость между выводами R и S компонента Q1 с количеством выводов больше 2 |
| QRS(Q1) | Заряд емкости между выводами R и S компонента Q1 с количеством выводов больше 2 |
| R(R1) | Сопротивление резистора R1 |
| C(X1) | Емкость конденсатора или диода Х1 |
| Q(X1) | Заряд конденсатора или диода Х1 |
| L(X1) | Индуктивность катушки индуктивности или сердечника Х1 |
| X(L1) | Магнитный поток в катушке индуктивности или сердечнике L1 |
| B(L1) | Магнитная индукция сердечника L1 |
| H(L1) | Напряженность магнитного поля в сердечнике L1 |
| RND | Случайное число с равномерным законом распределения на отрезке [0, 1]_ |
| ONOISE | Корень квадратный из спектральной плотности напряжения шума, отнесенного к выходу |
| INOISE | Корень квадратный из спектральной плотности напряжения шума, отнесенного ко входу, равный ОNOISЕ/коэффициент передачи по мощности |
| PG(V1) | Мощность, генерируемая источником V1 |
| PS(X1) | Реактивная мощность, накапливаемая в устройстве Х1 |
| PD(D1) | Мощность, рассеиваемая в устройстве D1 |
В этом перечне символы А и В обозначают номера узлов схемы, D1 — имя компонента с двумя выводами или управляемого источника, Q1 — имя любого активного устройства или линии передачи. Символы R и S заменяются аббревиатурами выводов устройств согласно таблице 2.3:
Таблица 2.3. Аббревиатуры выводов электронных компонентов
| Устройство | Аббревиатуры выводов | Названия выводов |
| МОП-транзистор (MOSFET) | D, G, S, В | Сток, затвор, исток, подложка |
| Полевой транзистор (JFET) | D, G, S | Сток, затвор, исток |
| Арсенид-галлиевый полевой транзистор (GaAsFET) | D, G, S | Сток, затвор, исток |
| Биполярный транзистор (BJT) | В, Е, С, S | База, эмиттер, коллектор, подложка |
| Биполярный транзистор с изолированным затвором (IGBT) | С, G, E | Коллектор, затвор, эмиттер |
| Линия передачи (Tran. Line) | АР, AM, ВР, ВМ | Вход+, вход–, выход+, выход– |
Например, следующие выражения означают: I(R1) — ток через резистор R1; R(Rload) — сопротивление резистора Rload; IC(Q1) — ток коллектора биполярного транзистора Q1; VBE(Q1) — напряжение между базой и эмиттером биполярного транзистора Q1, VGS(M1) — напряжение затвор-исток МДП-транзистора M1.
2.1.3. Математические выражения и функции
В сложных текстовых переменных директивы .DEFINE и при указании переменных, выводимых на графиках при проведении моделирования, возможно использование следующих математических операций.
Арифметические операции
+ — Сложение;
– — Вычитание;
* — Умножение;
/ — Деление;
DIV — Целочисленное деление;
MOD — Остаток целочисленного деления.
Тригонометрические, показательные, логарифмические функции от действительных и комплексных величин (х — действительная, z — комплексная величина)
Ехр(х) — экспонента;
Ln(x) — натуральный логарифм |х|;
Log(x) или Log10(x) — десятичный логарифм |х|;
Sin(x) — синус, х в радианах;
Cos(x) — косинус, х в радианах;
Таn(х) — тангенс, х в радианах;
Asin(x) — арксинус;
Acos(x) — арккосинус;
Atn(x) или Arctan(x) — арктангенс;
Atan2(y,x)= Atn(y/x) ;
Sinh(z) — гиперболический синус;
Cosh(z) — гиперболический косинус;
Tanh(z) — гиперболический тангенс;
Coth(z) — гиперболический котангенс.
Функции от комплексных величин (z)
DB(z) — величина в децибелах, равная 20*LOG(|z|);
RE(z) — действительная часть z,
IM(z) — мнимая часть z;
MAG(z) — модуль z. При построении графиков допустимо просто указать z;
PH(z) — фаза z в град.;
GD(z) — групповое время запаздывания.
Прочие функции от действительных и комплексных величин (x,y — действительная, z — комплексная величина, n,m — целые положительные)
ABS(y) — абсолютное значение у,
SQRT(y) — корень квадратный из модуля у,
SGN(y) — знак числа у,
POW(y,x) — степенная функция комплексных величин 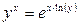 , обозначаемая как y^x;
, обозначаемая как y^x;
PWR(y,x) — действительная часть степенной функции y^x;
** — степенная функция, например 5**2=25;
PWRS(y,x) — действительная часть степенной функции y^x;
FACT(n) — факториал целого числа n;
RND— случайные числа на отрезке [0, 1] с равномерным законом распределения;
STP(x) — функция единичного скачка, равная 1 при T>x и равная 0 при T<=x. См. пример STP_SOURCE.CIR;
IMPULSE(y) — импульсная функция от аргумента у. Представляет собой импульс с нулевой длительностью фронтов, начинающий действовать в момент времени T=0, амплитудой y, и длительностью 1/y (т.е. площадь импульса всегда равна 1). См. пример IMPULSE_SOURCE.cir;
ТАВLЕ(х,х1,у1,х2,у2,...,хn,уn) — табличная зависимость функции у от х. Переменная х должна быть определена как параметр с помощью директивы .define Задаются координаты точек (хi, уi), в промежуточных точках используется линейная интерполяция. Если x<x1 то у=у1, если х>хn, то у=уn;
Waveform(<имя_файла>,у) — импорт функции у из файла <имя файла>, имеющего стандартный формат МС7; в этот файл пользователя (User source) могут быть записаны дискретизированные результаты моделирования, если на закладке Save Curves команды Properties (F10) выбрать из списка имя переменной и вести имя файла *.USR;
IМРОRТ(<имя_файла>,у) — импорт функции у из файла. Текстовый файл должен иметь формат выходного файла SPICE или МС7; в него помещается таблица значений переменных, в качестве которых может быть время (Т), частота (F), напряжение источника напряжений (V(имя источника)), ток источника тока (I(имя источника)), и выражение для у;
JN(n,z[,m]) — функция Бесселя л-го порядка первого рода комплексного аргумента z, полученная суммированием первых m членов ряда; по умолчанию m=10;
J0(Z) — функция Бесселя нулевого порядка первого рода комплексного аргумента z, аналогичная JN(0,z,10);
J1(z) — функция Бесселя первого порядка первого рода комплексного аргумента z, аналогичная JN(1,z,10);
YN(n,z[,m]) — функция Бесселя n-го порядка второго рода комплексного аргумента z, полученная суммированием первых m членов ряда; по умолчанию m=10;
Y0(z) — функция Бесселя нулевого порядка второго рода комплексного аргумента z, аналогичная YN(0,z,10);
Y1(z) — функция Бесселя нулевого порядка второго рода комплексного аргумента z, аналогичная YN(1,z,10);
Series(n,n1,n2,z) -- расчет текущей суммы ряда комплексной функции z=z(n) при изменении n от n1 до n2;
DIFA(u, v[,d]) — сравнение значений двух функций u и v во всех дискретных точках при расчете переходных процессов. DIFA присваивается значение 1, если во всех точках абсолютное значение разности функций меньше величины d, в противном случае присваивается 0. Параметр d необязательный, по умолчанию полагается d=0;
DIFD(u,v[,d]) — сравнение значений двух логических сигналов u и v во всех дискретных точках при расчете переходных процессов. DIFD присваивается значение 1, если во всех точках значения функций отличаются друг от друга, в противном случае присваивается 0. В течение первых d секунд после начала расчета переходных процессов сравнение не проводится. Параметр d необязательный, по умолчанию полагается d= 0.
Интегрально-дифференциальные операторы (x,y,u — действительные переменные)
DER(u,x) — производная переменной u по переменной x;
SUM(y,x[,sfart]) — текущий интеграл от переменной у по переменной х; начальное значение х равно start,
SD(y[,sfarf]) — текущий интеграл от переменной у по времени Т при анализе переходных процессов, по частоте F при АС-анализе или по переменной DCINPUT1 при DC-анализе; начальное значение независимой переменной равно start,
DD(y) — производная у по времени Т при анализе переходных процессов, по частоте F при АС-анализе частотных характеристик и по переменной DCINPUT1 при DC-анализе по постоянному току;
RMS(y[,sfarf]) — текущее среднеквадратичное значение величины y при интегрировании по времени Т при анализе переходных процессов (эквивалентно 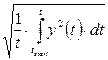 ), по частоте F при АС-анализе частотных характеристик и по переменной DCINPUT1 при DC-анализе по постоянному току; начальное значение независимой переменной равно значению start,
), по частоте F при АС-анализе частотных характеристик и по переменной DCINPUT1 при DC-анализе по постоянному току; начальное значение независимой переменной равно значению start,
AVG(y[,start]) — текущее среднее значение переменной у при интегрировании по времени Т при анализе переходных процессов (эквивалентно 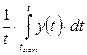 ), по частоте F при АС-анализе частотных характеристик; начальное значение независимой переменной равно значению start,
), по частоте F при АС-анализе частотных характеристик; начальное значение независимой переменной равно значению start,
SDT(y) — текущий интеграл процесса y(t) относительно времени Т, начиная от T=Tmin;
DDT(y) — производная процесса y(t) относительно времени Т;
DEL(y) — приращение процесса y(t) относительно предыдущей точки при расчете переходных процессов. Производная рассчитывается как отношение двух таких операторов, например производная dy/dt равна DEL(y)/DEL(t);
Операции отношения и логические операции (x,y — действительные величины, b — логическое выражение)
= — равно;
> — больше;
< — меньше;
>= — больше или равно;
<= — меньше или равно;
<> или != — не равно;
== — равно;
MIN(x,y) — минимальное значение величин х, у,
МАХ(х,у) — максимальное значение величин х, у,
LIMIT (u,х,у) — равно u, если х<u<у, равно х, если u<х; равно у, если u>у,
IF(b,x,y) — функция равна х, если b истинно, в противном случае равна у.
AND — логическое И;
NAND — отрицание логического И (И-HE);
NOT — отрицание;
OR — логическое ИЛИ;
NOR — отрицание логического ИЛИ (ИЛИ-НЕ);
XOR — исключающее ИЛИ;
Примечание: логическим выражениям присваиваются значения 1, если они истинны, и 0, если они ложны.
Операции с логическими переменными (состояниями цифровых узлов схемы)
HEX(A,B,C,D) — значение состояний цифровых узлов А, В, С, D в шестнадцатеричной системе;
BIN(A,B,C,D) — значение состояний цифровых узлов А, В, С, D в двоичной системе;
DEC(A,B,C,D) — значение состояний цифровых узлов А, В, С, D в десятичной системе;
OCT(A,B,C,D) — значение состояний цифровых узлов А, В, С, D в восьмеричной системе;
+ — сумма двух двоичных, восьмеричных, шестнадцатеричных или десятичных чисел;
– — разность двух двоичных, восьмеричных, шестнадцатеричных или десятичных чисел;
DIV — целочисленное деление двух двоичных, восьмеричных, шестнадцатеричных или десятичных чисел;
MOD — остаток после целочисленного деления двух двоичных, восьмеричных, шестнадцатеричных или десятичных чисел;
& — операция поразрядного логического И состояний двух цифровых узлов;
| — операция поразрядного логического ИЛИ состояний двух цифровых узлов;
^ — операция поразрядного логического исключающего ИЛИ состояний двух цифровых узлов.
~ — Операция поразрядного логического отрицания состояния цифрового узла
Операторы обработки сигналов (u, v — действительные сигналы при анализе переходных процессов, S — спектры сигналов)
HARM(u) — расчет гармоник сигнала u;
THD(S[,F]) — коэффициент нелинейных искажений спектра S, в процентах относительно уровня составляющей на частоте F; если частота F не указана, то относительно составляющей на частоте первой гармоники, равной 1/Тmax;
IHD(S[,F]) — коэффициент нелинейных искажений отдельных составляющих спектра S, в процентах относительно уровня составляющей на частоте F; если частота F не указана, то относительно составляющей на частоте первой гармоники, равной 1/Тmax;
FFT(u) — прямое преобразование Фурье дискретных отсчетов сигнала u(t). Отличается от функции HARM множителем N/2 для гармоник с первой до N-й и множителем N для нулевой гармоники, где N — количество дискретных отсчетов входного сигнала u(t);
IFT(S)— обратное преобразование Фурье спектра S;
CONJ(S) — сопряженный комплексный спектр S;
CS(u, v) взаимный спектр сигналов u и v, равный CONJ(FFT(v))*FFT(u)*dt*dt;
AS(u) — собственный спектр сигнала u(t), равный CS(u, u);
CC(u,v) — взаимная корреляционная функция сигналов u и v, равная IFT(CONJ(FFT(v))*FFT(u))*dt;
АС(u) — автокорреляционная функция сигнала и, равная IFT(CONJ(FFT(u))*FFT(u))*dt;
COH(u,v) — нормированная корреляционная функция сигналов u и v, равная CC(u,v)/sqrt(AC(u(0))*AC(v(0)));
REAL(S) — действительная часть спектра S, рассчитанного с помощью FFT;
IMAG(S) — мнимая часть спектра S, рассчитанного с помощью FFT;
MAG(S) — модуль спектра S, рассчитанного с помощью FFT;
PHASE(S) — фаза спектра S, рассчитанного с помощью FFT.
Параметры моделей
Параметры моделей компонентов можно вывести в текстовой форме или на графики, используя ссылки на них в виде: позиционное_обозначение_компонента.имя_параметра
Приведем несколько примеров:
Q1.bf — коэффициент усиления тока BF биполярного транзистора Q1;
М1.GAMMA — параметр GAMMA МОП-транзистора М1;
J1.VT0 — пороговое напряжение VT0 полевого транзистора J1.
В связи с тем, что в процессе моделирования параметры моделей компонентов не изменяются, их графики представляют собой прямые линии. Тем не менее, строить их имеет смысл при выполнении вариации параметров или статистических испытаниях по методу Монте-Карло, чтобы убедиться, что изменения параметров производятся в правильном диапазоне.
Правила использования выражений и переменных
1. Все параметры компонентов могут быть функцией времени Т (при анализе переходных процессов), произвольных напряжений и токов, температуры TEMP, комплексных переменной s и z (при анализе частотных характеристик).
Приведем примеры:
1.0/(1.0+.001*s) — передаточная функция фильтра низких частот, заданная с помощью преобразования Лапласа;
exp(-T/.5)*sin(2*PI*10*T) — функциональный источник затухающего гармонического сигнала с частотой 10 Гц;
5.0pF*(1+2e-6*T) — емкость конденсатора, зависящая от времени;
4.7K*(1+.3*V(P,M)) — сопротивление резистора, зависящее от напряжения;
2.6 uH*(1+2*(TEMP-273)^2) — индуктивность, зависящая от температуры;
V(VCC)*I(VCC) — мгновенная мощность источника напряжения VCC;
SUM(V(VCC)*I(VCC),T) — энергия источника VCC на интервале времени от 0 до Т;
FFT(V(A)+V(B)) — преобразование Фурье от V(A)+V(B));
RMS(V(Out)) — текущее среднеквадратическое значение напряжения V(Out));
IM(V(7)) — мнимая часть комплексного напряжения в узле 7;
MAG(VCE(Q1)*IC(Q1)) — модуль комплексной мощности, выделяемой на биполярном транзисторе Q1 при анализе частотных характеристик;
5*(Т>10 ns AND T<20 ns) — одиночный импульс с амплитудой 5В на интервале времени 10...20 нс;
5*((Т mod 50)>10 AND (T mod 50)<20) — импульс с амплитудой 5 В на интервале времени от 10 с до 20 с, период 50 с.
2. Значения операторов отношения и булевых операторов равно1.0, если они истинны, и 0.0, если они ложны.
3. Интегро-дифференциальные операторы (AVG, DEL, RMS и SUM…) могут использоваться только при выводе данных и не могут использоваться в выражениях для параметров.
4. ONOISE и INOISE могут использоваться только при АС анализе и их нельзя использовать в выражениях в совокупности с другими величинами, например с напряжениями.
5. При вычислении преобразования Фурье FFT в режиме АС (при этом рассчитываются импульсные характеристики как функции времени Т) графики других переменных (напряжений, токов и т. п.) строятся неправильно.
Поэтому их следует выводить на экран по отдельности в разных сеансах моделирования.
6. В АС анализе все промежуточные вычисления выполняются с комплексными величинами. Однако при построении графиков указание имени переменной означает построение графика ее модуля.
Например, указание имени переменной V(1) эквивалентно использованию функции вычисления модуля комплексной величины MAG(V(1)). И более того, спецификация выражения V(1)*V(2) приведет к построению модуля произведения двух комплексных напряжений. Для вывода мнимой части произведения используется запись IM(V(1)*V(2)), действительной части — RE(V(1)*V(2)).
7. При моделировании в режимах АС и DC значение переменной Т (время) полагается равной нулю. При расчете переходных процессов и в режиме DC равной нулю полагается переменная F(частота).
8. В выражениях для преобразования Лапласа передаточных функций может использоваться только символ S для обозначения комплексной переменной.
При отсутствии в выражении для такой передаточной функции символа S выдается сообщение об ошибке. Поэтому преобразования Лапласа нельзя использовать для задания линейных блоков с постоянным коэффициентом передачи — в этих целях используйте другие типы управляемых источников сигналов.
9. Комплексные величины можно использовать только в следующих функциях: +, –, *, /, sqrt, pow, In, log, exp, cosh, sinh, tanh, coth.
В функциях другого типа комплексные величины заменяются их действительными частями, например, функция действительного переменного SIN при наличии комплексного аргумента С1 равна sin(C1)=sin(RE(C1)).
10. Перед выполнением моделирования или составлением списка электрических соединений программа МС7 вычисляет значения всех операторов .DEFINE.
В связи с этим применение этих операторов внутри оператора .MODEL могут привести к ошибке. Пусть, например, имеются два оператора
.define BF 111
Дата добавления: 2017-09-19; просмотров: 246;
