Плоская гармоническая волна в диэлектрике

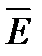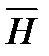Плоской называется электромагнитная волна, у кото­рой векторы поля и взаимно перпендикулярны и при соответствую­щем выборе направления осей координат будут зависеть только от одной пространственной координаты z и времени t.

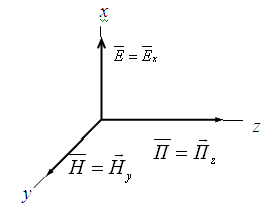
Волна распространяется в однородном диэлектрике (ε=сonst), прово­димость которого равна нулю ( 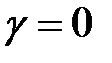). Выберем направления осей координат x, y, z так, чтобы вектор 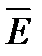совпа­дал с осью x 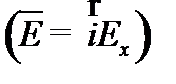, вектор 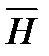совпадал с осью y 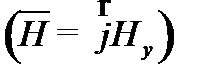, тогда вектор Пой­тинга будет направлен вдоль оси z.

Система уравнений Максвелла в комплексной форме:

Раскроем операцию rot в декартовой системе координат и учтем, что

векторы поля содержат только по одной пространственной составляющей: , :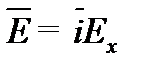

.

.

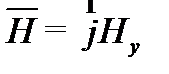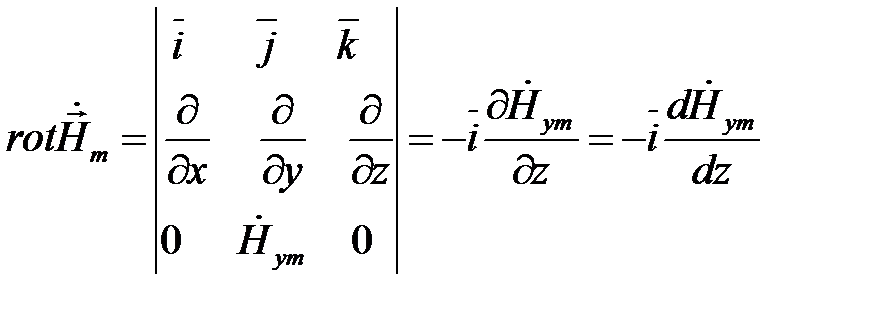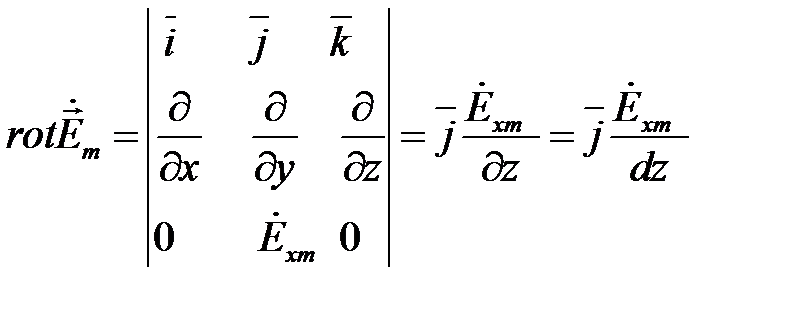Таким образом, система уравнений Максвелла получит вид:

Решим данную систему дифференциальных уравнений относительно пере­менной 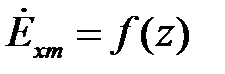. Для этой цели продифференцируем уравнение (2) по пе­ременной z и выполним в него подстановку из уравне­ния (1):

,

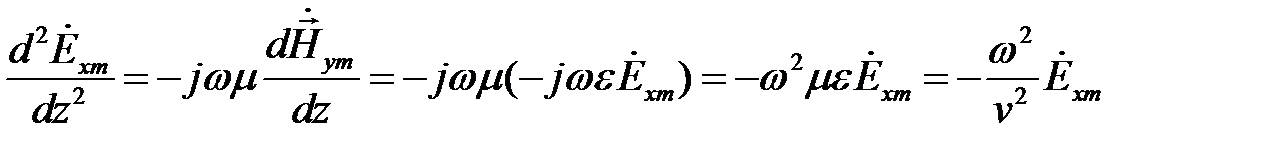где 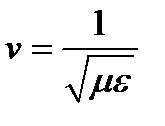- фазовая скорость волны.

Таким образом,

.

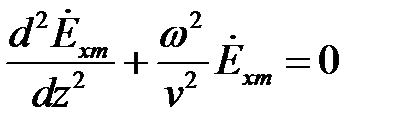Решение для искомой функции:

.

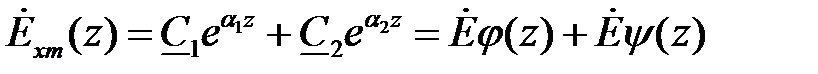где 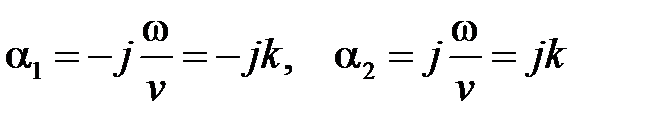- корни характеристического уравнения.

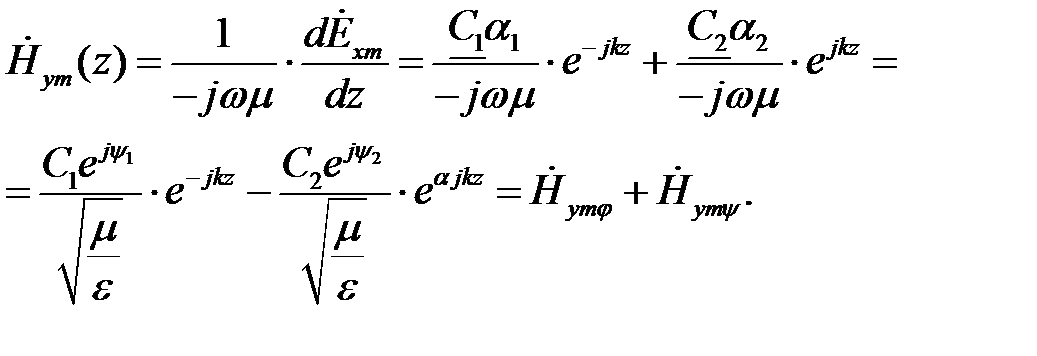
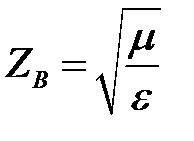— волновое сопротивление среды;

для пустоты Ом.;

Решение содержит электромагнитные волны:

прямую — H_ymφ; E_xmψ=Z_B H_ymφ и обратную — H_ymψ; E_xmψ=-Z_B H_ymψ.

В неограниченной однородной среде отраженные волны отсутствуют, поэтому при­мем С₂=0, С₁=Сe^jy, тогда решение для искомой функции получит окончательный вид:

, где .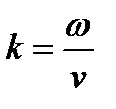

Решение для переменной 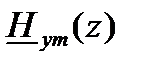получим из уравнения (2) путем подстановки в него найденного решения для переменной :

.

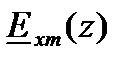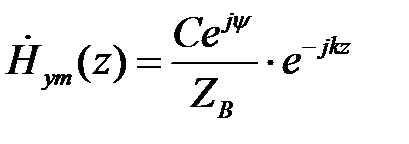Перейдем от комплексного изображения функций к их оригиналам:

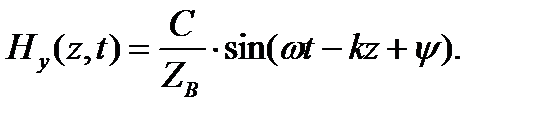
Таким образом, электромагнитное поле в диэлектрике распространяется в виде незату­хающих взаимно перпендикулярных в пространстве волн 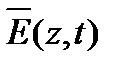и 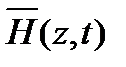со скоростью .

Отношение мгновенных значений волн 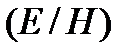в любой точке простран­ства и в любой момент времени равно волновому сопротивлению.

Длиной волны λ называют расстояние, на котором фаза волны изменяется на 2π: 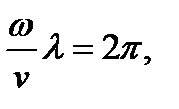откуда следует, что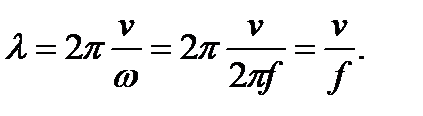

Каждая из волн переносит энергию в направлении своего движения, при этом объемные плотности энергий электрического и магнитного полей равны между собой.