Фундамент анализа систем
Если вы свободно оперируете понятиями «скалярное произведение функций», «преобразование Фурье», «преобразование Лапласа», то чтение данного параграфа стоит пропустить. Если же нет, то это как раз самый подходящий случай изучить эти фундаментальные понятия. Прежде всего под сигналом будем понимать функцию. Обычно это будет функция времени, и время мы будем считать пока непрерывным. Очень часто сигналы требуется сравнить друг с другом. Обычно нет смысла сравнивать сигналы поточечно по амплитуде – это вряд ли позволит ответить на вопрос, похож ли принятый сигнал на тот который мы ждем. Пусть, например, у нас есть два сигнала – просто синусоида и синусоида с добавленной к ней постоянной составляющей. Если предположить, что постоянная составляющая достаточно велика, то при поточечном сравнении амплитуд окажется что сигналы сильно различны. Однако на самом деле оба этих сигнала могут быть синусоидами одинаковой амплитуды и частоты! Для того чтобы «правильно» сравнивать сигналы удобно воспользоваться векторной абстракцией. У вектора есть направление и модуль. Как бы далеко не находились два одинаковых вектора, мы всегда можем их сравнить по модулю и направлению. Самым удобным в этом случае является использование скалярного произведения векторов, которое по определению равно произведению модуля одного вектора на модуль другого и на косинус угла между ними. Определить его очень легко: для этого нужно просуммировать все произведения соответствующих координат обоих векторов. Таким образом, скалярное произведение есть мера сонаправленности (схожести) векторов.
С другой стороны, любой вектор есть не более чем набор чисел. Если любую функцию мы можем представить бесконечным количеством ее значений, то функция также есть вектор, а стало быть, мы можем подсчитать скалярное произведение между двумя функциями:
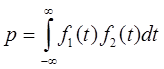
| (1.1) |
Впервые такое представление о функциях ввел итальянский математик Вольтерра. Таким образом, скалярное произведение двух функций есть мера их «похожести».
Теперь перейдем к преобразованиям сигналов (функций). Для преобразования будем использовать понятие оператора, или, что то же самое, ориентированную систему.
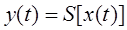
| (1.2) |
Здесь x(t) – есть независимый входной сигнал, а y(t) – выходной результат преобразования S. Если преобразование S является линейным (понятие линейной системы подробно обсуждается далее в этом пособии), то практически все сигналы, проходя через нее, будут как-то менять свою форму. Но есть одно исключение – функция 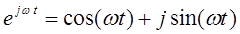 - комплексная экспонента. Эта функция, проходя сквозь линейную систему S, не меняет свою форму, а меняет только амплитуду и фазу. Если трактовать эту функцию как вектор, то она называется собственным вектором преобразования S.
- комплексная экспонента. Эта функция, проходя сквозь линейную систему S, не меняет свою форму, а меняет только амплитуду и фазу. Если трактовать эту функцию как вектор, то она называется собственным вектором преобразования S.
Ввиду такой особенности этой функции было бы удобным все функции, проходящие сквозь линейную систему, рассматривать как совокупность таких комплексных экспонент.
Как же разложить наш произвольный сигнал на набор комплексных экспонент? Ответ прост: надо воспользоваться скалярным произведением. Если взять набор комплексных экспонент с единичной амплитудой и разными частотами, то скалярное произведение кождой из них на наш сигнал как раз и даст меру присутствия комплексной экспоненты такой частоты в нашем сигнале:

| (1.3) |
Формула (1.3) задает прямое преобразование Фурье. Так как каждая комплексная экспонента, проходя через линейную систему, изменяется только по амплитуде и фазе, то мы можем получить амплитуду и фазу для каждой частотной составляющей выходного сигнала путем простого умножения:
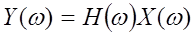 , ,
| (1.4) |
где 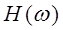 - частотная характеристика системы, определяющая, как изменяется по амплитуде и по фазе комплексная экспонента заданной частоты.
- частотная характеристика системы, определяющая, как изменяется по амплитуде и по фазе комплексная экспонента заданной частоты.
Существует также и обратное преобразование Фурье. Оно задается формулой:
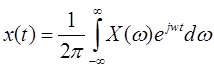
| (1.5) |
Попробуйте самостоятельно ответить на вопрос: какую смысловую нагрузку несет в себе знак минус в степени экспоненты в прямом преобразовании Фурье и почему его нет в обратном?
Каждой линейной системе S соответствует некоторое линейное дифференциальное уравнение. Известно, что общее решение любого линейного уравнения есть взвешенная сумма функций 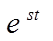 , где
, где 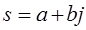 - некоторое комплексное число, являющееся корнем характеристического уравнения для этого дифференциального уравнения. По этой причине, при изучении системы с помощью дифференциального уравнения было бы удобным представить входной сигнал и выходной сигнал (решение уравнения) в виде суммы функций
- некоторое комплексное число, являющееся корнем характеристического уравнения для этого дифференциального уравнения. По этой причине, при изучении системы с помощью дифференциального уравнения было бы удобным представить входной сигнал и выходной сигнал (решение уравнения) в виде суммы функций 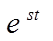 . Т.е. необходимо наши сигналы-векторы вновь разложить по некоторому базису функций-векторов, на этот раз зависящих от переменной s. Такое разложение носит имя прямого преобразования Лапласа:
. Т.е. необходимо наши сигналы-векторы вновь разложить по некоторому базису функций-векторов, на этот раз зависящих от переменной s. Такое разложение носит имя прямого преобразования Лапласа:
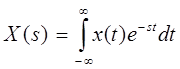
| (1.6) |
Ему соответствует обратное преобразование:
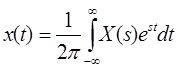
| (1.7) |
Преобразование Лапласа также называют переходом в область изображений. В этой области операция дифференцирования заменяется умножением на s, а интегрирование – делением на s. Поэтому соотношение (1.4) можно обобщить:
 , ,
| (1.8) |
где функция H(s) называется передаточной функцией системы S. Такое представление линейной системы, как мы увидим позже, позволяет упростить решение большинства задач обработки сигналов.
Таковы замечательные свойства комплексной экспоненты относительно линейных преобразований. Ключевыми моментами здесь являются: представление функции как вектора, использование скалярного произведения для перехода к новым системам координат, использование специфических свойств комплексной экспоненты. Все это вместе и ничего больше составляет фундамент анализа линейных систем. А теперь перейдем к основам цифровой обработки сигналов.
Дата добавления: 2017-08-01; просмотров: 413;
