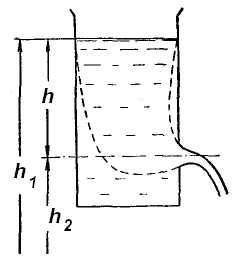
Применим уравнение Бернулли к случаю истечения жидкости из небольшого отверстия в широком открытом сосуде.
| 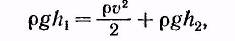 Или
Или
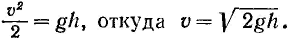 (18.8) –
Формула Торричелли (18.8) –
Формула Торричелли
|
| рис. 18.4 |
Вязкость. Формула Ньютона. Стационарное течение жидкости по прямолинейной трубе. Формула Пуазейля.
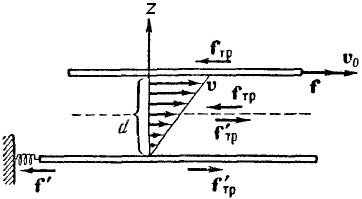 рис. 18.5 Силы внутреннего трения
рис. 18.5 Силы внутреннего трения
| Варьируя скорость пластины v0, площадь пластин. S и расстояние между ними d, можно получить, что 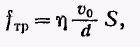 (18.9)
Или (18.9)
Или
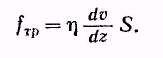 (18.10) (18.10)
|
Единицей вязкости в СИ является такая вязкость, при которой градиент скорости, равный 1 м/сек на 1 м, приводит к возникновению силы внутреннего трения в 1 Нна 1 м2 поверхности касания слоев.
Движение жидкости по трубе. Формула Пуазейля
При не слишком больших скоростях течения изменяется вдоль любого радиуса по закону
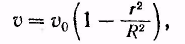 (18.11)
(18.11)
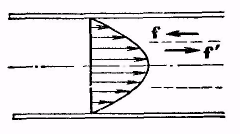 рис. 18.6
рис. 18.6
| Части жидкости, лежащие по разные стороны от этой поверхности, действуют друг на друга, с силой, величина которой в расчете на единицу поверхности равна
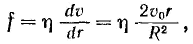 (18.12)
т. е. возрастает пропорционально расстоянию поверхности раздела от оси трубы. (18.12)
т. е. возрастает пропорционально расстоянию поверхности раздела от оси трубы.
|
Сила внутреннего трения
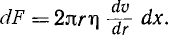
Сила разности давлений dF:
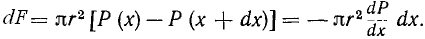
При стационарном течении сумма этих двух сил должна обращаться в нуль, поэтому
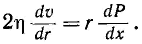
Скорость u (r), а с ней и производная 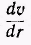 не меняются с изменением х.
не меняются с изменением х.
Поэтому должна быть постоянной и производная 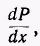 причем эта производная должна быть равна
причем эта производная должна быть равна 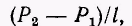 где P1 — давление на входе трубы, Р2 — на выходе, а l — длина трубы. В результате приходим к уравнению
где P1 — давление на входе трубы, Р2 — на выходе, а l — длина трубы. В результате приходим к уравнению
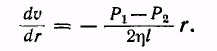
Интегрируя, получим
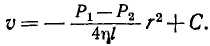
Постоянная интегрирования С определится из условия, что на стенке трубы, т. е. при r = R скорость v должна обращаться в нуль. Это дает
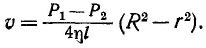 (18.13)
(18.13)
Скорость v максимальна на оси трубы, где она достигает значения
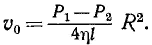 (18.14)
(18.14)
При удалении от оси скорость v меняется по параболическому закону.
Расход жидкости
Определим расход жидкости, т. е. количество ее, ежесекундно протекающее через поперечное сечение трубы.
Масса жидкости, ежесекундно протекающая через кольцевую площадку с внутренним радиусом r и внешним r + dr, равна
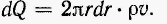
Подставляя сюда выражение для u(18.13)и интегрируя, находим искомый расход жидкости
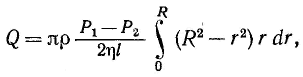
Или
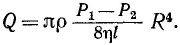 (18.15)
(18.15)
Расход жидкости пропорционален разности давлений Pt — Р2, четвертой степени радиуса трубы и обратно пропорционален длине трубы и коэффициенту вязкости жидкости.
Формула (18.15) называется формулой Пуазейля, хотя сам Пуазейль и не выводил ее, он исследовал вопрос только экспериментально. На формуле Пуазейля основан один из экспериментальных методов определения коэффициентов вязкости жидкостей.
Дата добавления: 2017-06-02; просмотров: 671;
