Уравнение Бернулли. Силы внутреннего трения. Коэффициент вязкости. Течение жидкости в круглой трубе. Формула Стокса.

Источники: Детлаф Яворский 2002 г., Пар. 3.5 С. 44-46.

Савельев И. В., Т.1 Механика, колебания и волны, молекулярная физика, Глава «Гидродинамика»

Лагранжев и Эйлеров способ описания движения.

Поле векторов скорости, линии тока.

Густота линий тока.

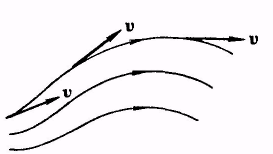
рис. 18.1. Линии тока

Если вектор скорости в каждой точке пространства остается по­стоянным, то течение называется установившимся, или стационарным.

рис. 18.2. Трубки тока

Объемы жидкости, протекающие за еди­ницу времени через сечения S₁ и S₂, должны быть одинаковы:

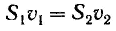
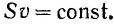(18.1)

Выражение (18.1) представляет собой содержание теоремы о неразрывности струи.

Жидкость, в которой внутреннее трение (вязкость) полностью отсутствует, называется идеальной.

Уравнение Бернулли

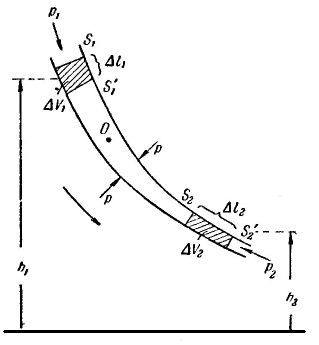
рис.18.3

Приращение энергии запишется следующим образом:

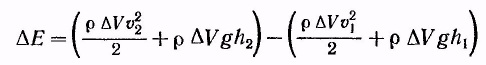(18.2)

Работа:

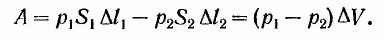(18.3)

Приравнивая выражения (18.2) и (18.3), сокращая на DV и перенося члены с одинаковыми индексами в одну часть равенства, получим:

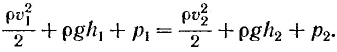(18.4)

Полученный нами результат можно сформулировать следующим образом: в стационарно текущей идеальной жидкости вдоль любой линии тока выполняется условие

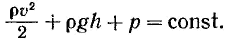(18.5)