Енергія і робота при обертальному русі

Кінетична енергія. При обертанні навколо нерухомої осі кінетична енергія визначається формулою

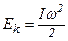, (1.64)

де I – момент інерції тіла навколо цієї осі, 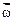– кутова швидкість.

У загальному випадку рух тіла – це накладання двох рухів – поступального з швидкістю центра інерції 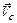й обертального з кутовою швидкістю w навколо осі, яка проходить через центр інерції тіла.

У цьому випадку формула для кінетичної енергії отримує найбільш простий вигляд:

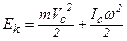, (1.65)

де 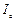– момент інерції відносно осі обертання, що проходить через центр інерції тіла.

Таким чином, у загальному випадку руху тіла його кінетична енергія складається з кінетичної енергії поступального руху і кінетичної енергії обертального руху навколо осі, яка проходить через центр інерції тіла.

Робота при обертання твердого тіла. Якщо результуючий момент сил 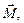які діють на тіло, не змінюється ( 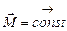), то робота при обертанні:

A = Mj, (1.66)

де j – кут повороту. Якщо результуючий момент M є змінною величиною, то весь кут повороту потрібно розбити на елементарні повороти Dj_i , такі малі, що моменти сил M_i на цих ділянках можна вважати незмінними величинами. Тоді для кожної i-ї ділянки можна застосувати формулу (1.66), а повна робота буде дорівнювати:

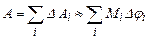. (1.67)

Формула (1.67) тим точніше визначає роботу, чим менші Dj_i. Строгий знак рівності можна поставити тільки під знаком границі при Dj_i ®0. В результаті отримаємо:

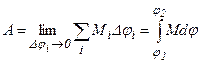, (1.68)

де j₁ і j₂ – початковий і кінцевий кути повороту. Таким чином, щоб визначити роботу при обертальному русі, потрібно результуючий момент сил, що діють на тіло, проінтегрувати за кутом повороту.

На координатній площині (M, j) робота чисельно дорівнює

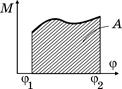
Рис. 13

площі криволінійної трапеції, яка зверху обмежена графіком M=f(j), знизу віссю кутa повороту, ліворуч і праворуч прямими j = j₁ і j = j₂ (див. рис. 13).