и ускорения общего центра масс тела от времени в цикле ходьбы

КИНЕМАТИКА ЛОКОМОЦИЙ

Одной из основных задач биомеханики при исследовании движений чело­века является измерение количественных показателей механического состояния биосистемы и его изменения. Существующие методы регистрации движений (оптическое, механоэлектрическое и т.д.) позволяют определить кинематические и динамические характеристики движений спортсмена.

Кинематика движений определяет пространственную форму движений и ее изменение во времени без учета масс тела и действующих на него сил и мо­ментов сил. Кинематика дает только внешнюю картину движения и не раскры­вает причину изменения движений, и механизмы, лежащие в основе этих движе­ний.

Кинематические характеристики тела человека и его движений – это меры положения и движения человека в пространстве и во времени: пространствен­ные, временные и пространственно-временные.

1.1 Описание положения тела

Положение тела человека в пространстве описывается тремя характеристи­ками: местом, ориентацией и положением (рис. 1).

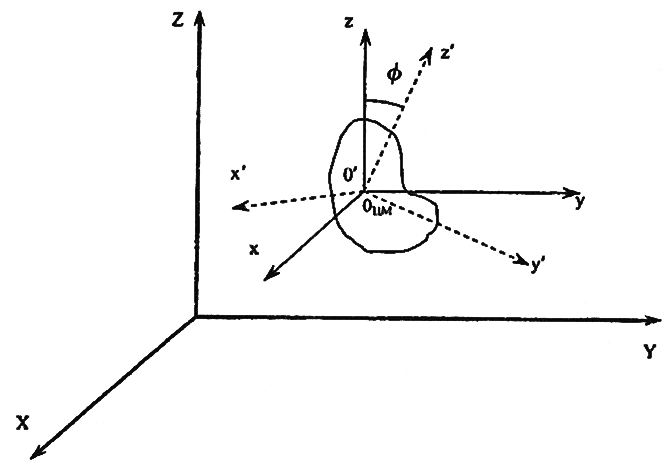
Рис. 1. Неподвижная (XYZ) и подвижная (xyz) системы координат, характеризующие место тела в пространстве

Место тела характеризует, в какой части пространства в данный момент находится человек (например, в какой части стадиона). Чтобы определить место тела, достаточно указать три координаты какой-либо точки тела в неподвижной системе координат. В качестве такой точки выбирают общий центр масс тела (ОЦМ), связывая с ним начало координат другой подвижной системы координат, оси которой ориентированы так же, как и оси неподвижной системы (рис. 1).

Ориентация тела характеризует его поворот относительно неподвижной системы координат. На рисунке 1 показано, что подобный поворот подвижной системы координат можно оценить по величине угла φ (угол между соответству­ю­щими осями x y z и x¹ y¹ z¹). Например, при вращении подвижной системы ко­ординат в плоскости ХОУ величина угла φ₁ = 0, что означает ориентацию тела вверх головой, при φ₂ = 90° – горизонтально, при φ₃ = 180 – вниз головой.

Поза тела характеризует взаимное расположение звеньев тела относи­тельно друг друга. Анатомическое описание поз в анатомии весьма условно (сги­бание-разгибание и т.д.), биомеханическое описание основано на применении системы независимых углов Эйлера, описывающих движение в суставах в трех­мерном пространстве. Определение действительных значений углов Эйлера для сегментов тела человека при движении в трехмерном пространстве позволяет ис­пользовать аппарат теоретической механики для решения многочисленных задач биомеханического исследования.

1.2 Система координат: инерциальная, связанная с телом, поточная

При описании положения тела необходимо выбрать неподвижную систему координат. Эту неподвижную систему координат связывают с телом отсчета (условно взятым телом, от которого отсчитывается расстояние). На теле отсчета устанавливают начало и направление измерения расстояния, выбирают единицы отсчета (все это в совокупности составляет систему отсчета).

Однако любое тело отсчета нельзя считать абсолютно неподвижным и на отсчет расстояний будет влиять движение самого тела отсчета с ускорением. Условно принято считать «неподвижным», не ускоряемым телом отсчета такое, ускорение которого мало и не сказывается на отсчете данного наблюдаемого движения. Для «неподвижной» (инерциальной) системы координат справедливы формулы Ньютона (законы Ньютона).

Рассматривая подвижное тело отсчета и связанную с ним систему коорди­нат (неинерциальное тело отсчета), заметим, что ускоренное их движение при­водит к существенным влияниям на изучаемые характеристики. Законы Ньютона для неинерциального тела отсчета не соблюдаются. Примером неинерциальной системы координат (связанной с телом) может служить система координат, начало отсчета которой находится в точке тазобедренного сустава перемещаю­щегося спортсмена, относительное движение центра масс бедра будет рассмат­риваться в неинерциальной системе координат.

Поточная система координат неподвижно связана с основной плоскостью движения какого-либо сегмента тела человека (например, плоскостью ладони при плавании). Необходимость введения такой системы координат обусловлена решением задач динамики и определения сил аэродинамического сопротивления (рис. 2).

Рис. 2. Поточная система координат

1.3 Кинематические характеристики

Пространственный рисунок движения точки определяет ее траектория (во­ображаемый след движущейся точки). Длина траектории – это путь точки. Путь точки в криволинейном движении равен длине кривой линии от начального до конечного положения. Кривизна траектории (K) показывает, какова форма дви­жения в пространстве, определяется по радиусу кривизны (r) из следующего со­отношения:

.

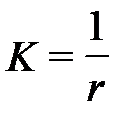Перемещение точки измеряется по разности координат: ΔS = S_K – S_H (м) для поступательного движения; Δϕ = ϕ_K – ϕ_Н (град) для вращательного движения, где S_K, S_H – конечная и начальная линейные координаты; ϕ_K, ϕ_Н – конечная и началь­ная угловые координаты.

Временные характеристики, раскрывающие движение во времени, опреде­ляются при наличии системы отсчета времени, где за начало отсчета берется точка временной оси, отражающая начало движения.

К временным характеристикам относят:

- момент времени (t_i) – точка на временной оси – промежуток времени от начала отсчета до него;

- длительность движения (Δt) – разность моментов времени от начала (t₁) до конца движения (t₂):

Δt = t₂ – t₁;

- темп движений – временная мера повторности движений (N) – количес­тво движений в единицу времени:

,

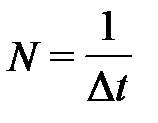· где единицей времени служит минута (например, критический темп в спортивной ходьбе составляет 230 шагов в минуту);

- частота движений – временная мера повторности движений (f) – коли­чество движений в единицу времени:

,

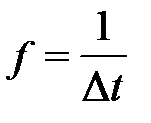· где единицей времени является секунда (например, максимальная ча­стота шагов в спринтерском беге составляет 4,8 шаг/с);

- ритм движений – соотношение длительностей частей движений (фаз или периодов):

R = Δt₁ : Δt₂ : Δt₃…

Фаза – это часть движения, на протяжении которой решается определенная двигательная задача. Начало и окончание фазы находят по граничным моментам, моментам существенного изменения движения. Граничные моменты выявля­ются при анализе изменения во времени динамических и энергетических харак­теристик основных точек тела человека (например, общего центра масс тела) и фиксируют нулевые и экстремальные (минимальные и максимальные) величины перечисленных биомеханических характеристик. Например, момент отрыва и момент постановки ноги на опору в беге, максимальная H_max и минимальная H_min координаты перемещения общего центра масс тела человека при ходьбе в верти­кальной плоскости.

Графическое представление временной структуры движения иллю­стриру­ется с помощью хронограммы (временной диаграммы движения) (рис. 3).

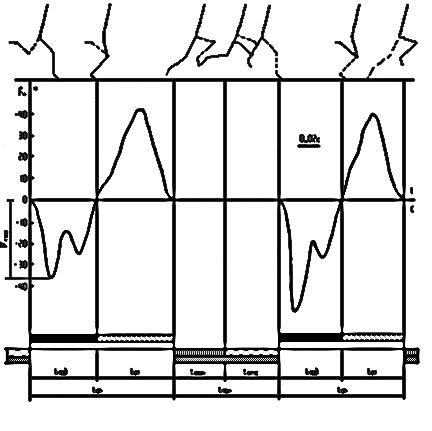
Рис. 3. Временная диаграмма движения (хронограмма)

Скорость и ускорение – это пространственно-временные характеристики движения. Скорость определяет быстроту изменения положения точки в про­странстве с изменением времени:

.

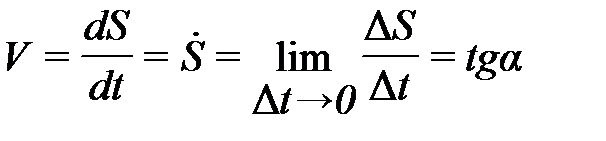Скорость – это первая производная пути по времени. Графически первая производная может быть определена по тангенсу угла наклона касательной в лю­бой точке зависимости S = S (t) – так определяется мгновенная скорость. Средняя скорость на отрезке или внутрицикловая скорость для циклических локомоций рассчитывается из соотношения перемещения точки за отрезок времени, в тече­ние которого это изменение произошло. Максимальная скорость V_max может быть определена графически по тангенсу угла наклона касательной (на графике пере­мещений S = S (t)), равному нулю – в точках экстремума tgα = 0.

Рассмотрим графики изменения вертикальных перемещений, скорости и ускорения ОЦМ тела ходока в цикле ходьбы во времени (рис. 4).

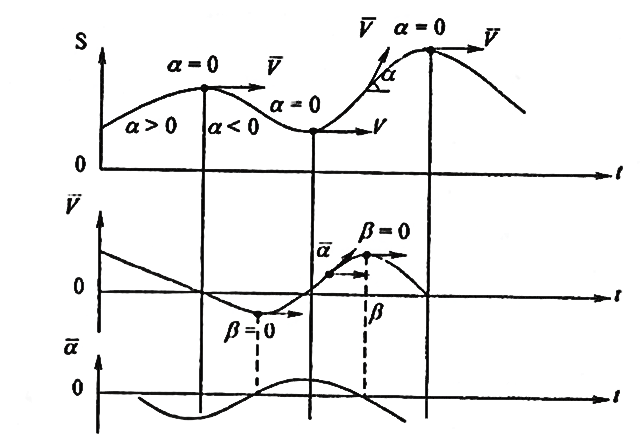
Рис. 4. Графики зависимости вертикального перемещения скорости

и ускорения общего центра масс тела от времени в цикле ходьбы

Знак скорости показывает направление движения: (+) – вверх, (–) – вниз (по графику вертикальных перемещений ОЦМ).

Знак ускорения показывает направление действия силы в ОЦМ. Если знак скорости и ускорения совпадают в какой-либо части движения (фазе), то движе­ние имеет ускоренный характер; если знаки противоположны, т.е. направление движения и действующая сила разнонаправлены, то имеет место торможение.

Ускорение характеризует быстроту изменения вектора скорости в данный момент времени:

.

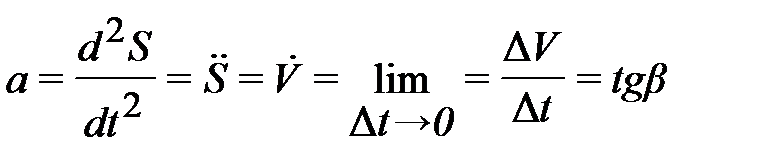Ускорение в точке может быть вычислено графически по тангенсу угла наклона кривой скорости, изменяющейся во времени:

.

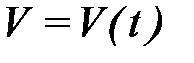Для гармонической (синусоидальной) функции изменения перемещения во времени графики перемещений и ускорений находятся в противофазе (как видно из рисунка 4) – это следствие двойного дифференцирования гармонической функции.

Рассмотрим взаимосвязь величин скорости и ускорения для поступатель­ного и вращательного движений, представленную в таблице 1.

Таблица 1

Поступательное движение	Вращательное движение	Взаимосвязь показателей
Линейная координата (м)	Угловая координата (град, рад)	Радиус окружности (м)
Si	φi	R
Линейная скорость (м/с)	Угловая скорость (град/с)	–
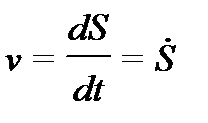
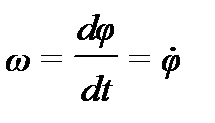
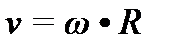
Линейное ускорение	Угловое ускорение	–

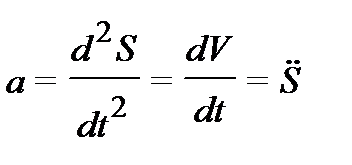
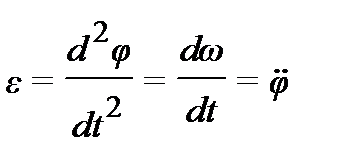
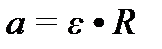
1.4 Длина и частота шагов. Связь длины и частоты шагов со скоростью

В циклических локомоциях (ходьба, бег, коньки, лыжи, гребля) скорость передвижения зависит от длины и частоты шагов.

Под длиной шага будем понимать расстояние, которое проходит спорт­смен, велосипед или лодка за один цикл движения. Соотношение длины и ча­стоты шагов в различных способах передвижения неодинаковы, но существуют общие закономерности: с увеличением частоты шагов усиливается отталкива­ние, растет длина шагов и вследствие этого возрастает скорость. Одновременное повышение частоты шагов и длина шага возможно до некоторого предела, после которого дальнейшее повышение одного параметра приводит к снижению дру­гого.

Оптимальная скорость шагательных локомоций определяется оптималь­ным соотношением длины и частоты шагов, при которых наблюдаются мини­мальные затраты энергии на передвижение.