Предел функции в бесконечности и в точке.

Определение.Число называется пределом функции при , если для любого сколь угодно малого положительного числа существует такое положительное число N, зависящее от ε - N(ε), что для всех x, таких что выполняется неравенство .(Рис.2)

Кратко это определение можно записать так:

Геометрический смысл предела

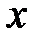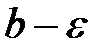При достаточно больших х, значение функции мало отличается от . (Ординаты лежат в полосе b-ε< < b+ε)

Пусть дана функция , определенная в проколотой окрестности точки .

Определение.Число называется пределом функции в точке (при ), если для любого сколь угодно малого числа существует δ, зависящее от ε - такое, что для всех , удовлетворяющих соотношению , выполняется неравенство .(Рис. 3)

Обозначение: .

Геометрический смысл предела

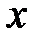Найдется такая δ-окрестность точки x₀, что для всех х из этой окрестности, соответствующие ординаты функции будут заключены в полосе b-ε< < b+ε).

Пример 1. Доказать: .

Доказательство. Для любого имеем:

.

Таким образом, для любого существует такое, что как только . Следовательно, .

Определение.Число называется пределом функции при слева, если для любого сколь угодно малого числа существует такое , что для всех , удовлетворяющих соотношению , выполняется неравенство .

Обозначение: .

Определение 2.Число называется пределом функции при справа, если для любого сколь угодно малого числа существует такое , что для всех , удовлетворяющих соотношению , выполняется неравенство .

Обозначение: .

Замечание 1. Если функция имеет в точке оба односторонних предела, которые равны между собой и равны числу , то функция имеет в точке предел равный .

Замечание 2. Определение предела в точке не требует существования самой функции в этой точке (т.е. изучает поведение функции в окрестности этой точки).

Бесконечно малые и бесконечно большие функции

Определение. Функция называется бесконечно малой величиной (БМВ) при или при 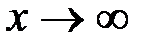, если ее предел равен нулю:

.

Свойства бесконечно малых величин:

- алгебраическая сумма конечного числа бесконечно малых величин есть величина бесконечно малая;

- произведение БМВ на ограниченную функцию есть БМВ;

- частное от деления БМВ на функцию, предел которой отличен от 0, есть БМВ.

Пример. Функци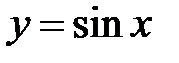и и являются б/м при , т.к. и .

Определение 2. Функция называется бесконечно большой величиной (ББВ) при или при 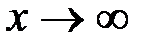, если ее предел равен бесконечности.

!!! Если - БМВ при или при 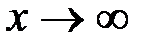, то функция является ББВ при или при 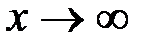. Верно и обратное утверждение.

Свойства бесконечно больших величин:

- сумма ББВ и ограниченной функции, есть ББВ;

- произведение ББВ на функцию, предел которой отличен от 0 есть ББВ;

- частное от деления ББВ на функцию, имеющую предел, есть ББВ.