Mathematical Models of Static (MMS) of objects
Problem definition of modeling and identification of static characteristics of objects (cm figure 2.1).
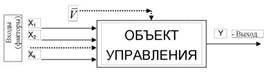
Figure 2.1 Structure of an object of a statics
Математические модели статических (MMS) объектов
Определение проблемы моделирования и идентификации статических характеристик объектов (см рисунок 2.1).
| L; LЗН equation; |
Characteristic of a MMS is that in them there are no derivatives on time.
In a general view of a MMS of an object – the function of a response connecting input parameters of X with entrance Y = j( X1, X 2 ...X K ) in the presence of a vector of
indignations of V. When using the MM statistical methods of a statics it is usually presented in the regression equation form (a polynomial, a piece of a number of Taylor in which function decays):
Характеристика в MMS является то, что в них нет производных по времени.
В общем виде в MMS объекта - функция ответа, соединяющего входные параметры Х с входной Y (X1, X 2 ... X K) в присутствии вектора
возмущений V. При использовании ММ статистические методы статики это обычно представляется в виде уравнения регрессии (многочлен, кусок ряда Тейлора, в котором функция затухает):
| k | k | kk | |||
| = b0 | +еbi Ч X i +еbii Ч X i2+е еbij Ч X i Ч X j (2.1) | ||||
| Y | |||||
| i =1 | i =1 | i =1 j =i +1 |
in the regression
(2.2)
The choice of model of a look (2.2) is caused by his simplicity, and, rather big accuracy of the description of the studied dependences. The look (1) is traditionally used, if necessary (if the
equation not adequately describes an experiment) members of a look bi Ч X i3 , b j Ч X1Ч X 2Ч X 3, etc. can be added. Special computing difficulties when determining values
of coefficients of bi of the equation of regression of bi at the same time don't arise, however, the nature of change of behavior of a function graph of high orders outside the range of approximation and even between the points found experimentally can at once baht is unpredictable.
Mathematical models of linear dynamic (MMD) objects and systems and communication between them. MMD.
Are widely used in the analysis and synthesis of various systems of automation (see the figure 2.2). MMD describe change of parameters in time, in their expressions surely are present derivatives on time or other parameters equivalent to them
Выбор модели внешний вид (2.2) обусловлена его простотой, и, довольно большая точность описания изучаемых зависимостей. Выражение (1) традиционно используется, при необходимости (если
Уравнение не адекватно описывает эксперимент) члены выглядят би X i3, X 2 X 3 и т.д. могут быть добавлены б J X1. Особые трудности вычислений при определении значения
коэффициентов Bi уравнения регрессии Bi в то же время не возникает, однако, характер изменения поведения графика функции высших порядков вне диапазона приближения и даже между точками найденных экспериментально можно сразу батов непредсказуема.
Математические модели линейных динамических (ММР) объектов и систем и связи между ними. MMD.
Широко используются при анализе и синтезе различных систем автоматики (смотрите рисунок 2.2). MMD описывают изменение параметров во времени, в их выражениях, конечно, присутствуют производные по времени или другим параметрам эквивалентные им

| U(t) | X(t) |
| Объект |
Figure 2.2. Dynamics object
It is accepted to designate vectors of entrance influences by a letter U (control), vectors of output influences of a letter X (state) or Y (exits), vectors of the revolting influences of a letter V (in the figure 2.2 – aren't shown)
Дата добавления: 2017-05-18; просмотров: 585;
