Другие виды степенных средних величин
Наряду со средней арифметической, в статистике применяется средняя гармоническая величина, обратная средней арифметической из обратных значений признака. Как и средняя арифметическая, она может быть простой и взвешенной.
Формула для расчета средней гармонической простой будет иметь вид:
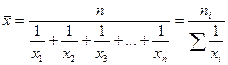
Формулу для расчета средней гармонической взвешенной можно представить в общем виде:
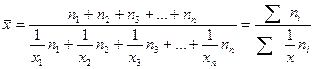
Например, имеются следующие данные:
| Выпуска продукции, тн. | Производительность труда, тн./чел.-час | |
| Цех 1 | ||
| Цех 2 | ||
| Итого |
Необходимо определить среднюю производительность труда. Для решения этой задачи необходимо пользоваться средней гармонической взвешенной:
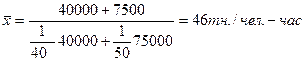
Средняя хронологическаяприменяется для оценки среднего уровня ряда динамики. При наличии информации на моменты времени с равными интервалами между ними используется средняя хронологическая простая:
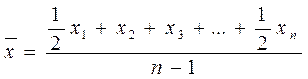 , где
, где
n – число моментов (дат)
Средняя геометрическая применяется, как правило, для оценки среднего показателя относительных величин (например, средний темп роста).
Средняя геометрическая простая определяется по формуле:
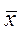

Средняя геометрическая взвешенная определяется по формуле:
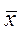
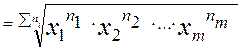
Средняя квадратическая применяется для определения средних размеров диаметров труб стальных, стволов деревьев и т.д. Этот вид средней также используется при расчете показателей вариации
· простая:
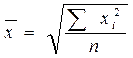
· взвешенная:
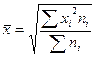
При расчете различных степенных средних по одним и тем же данных статистического наблюдения средние не буду одинаковы. Чем выше степень k средней, тем больше ее величина. Математически доказано, что между величинами степенных средних, рассчитанных по одной и той же совокупности единиц статистического наблюдения и одному и тому же признаку, существует следующее соотношение:
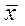 гарм <
гарм < 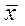 геом <
геом < 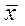 ар <
ар < 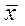 кв.
кв.
Мода и медиана
Для характеристики структуры совокупности применяются особые показатели, которые можно назвать структурными средними. К таким показателям относятся мода и медиана.
Мода - это величина признака (варианта), наиболее часто повторяющаяся в изучаемой совокупности. Для дискретных рядов распределения модой будет значение варианта с наибольшей частотой.
Например, если совокупность состоит из значений:
2,4,5,4,5,3,2,4,5,5,5,4,4,3,3,2,3,4
то мода равна 4, поскольку повторяется больше всех (6 раз)
Для дискретных рядов распределения модой будет значение варианта с наибольшей частотой.
Для интервальных рядов распределения с равными интервалами мода определяется по формуле:
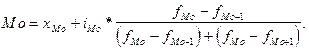
где 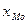 - начальное значение интервала, содержащего моду;
- начальное значение интервала, содержащего моду;
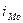 - величина модального интервала;
- величина модального интервала;
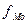 - частота модального интервала;
- частота модального интервала;
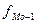 - частота интервала, предшествующего модальному;
- частота интервала, предшествующего модальному;
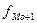 - частота интервала, следующего за модальным.
- частота интервала, следующего за модальным.
При этом модальным интервалом называется интервал с наибольшей частотой.
Медиана - это варианта, расположенная в середине упорядоченного вариационного ряда. Если ряд распределения дискретный и имеет нечетное число членов, то медианой будет варианта, находящаяся в середине упорядоченного ряда (упорядоченный ряд - это расположение единиц совокупности в возрастающем или убывающем порядке).
Рассмотрим пример расчета медианы в дискретном ряду.
Определим медиану заработной платы рабочих.
| Месячная з/п , руб. | Число рабочих | Сумма накопительных частот |
| 8 (2+6) | ||
| 24 (8+16) | ||
| — | ||
| — | ||
Для определения медианы надо подсчитать сумму накопленных частот ряда. Наращивание итога продолжается до получения накопленной суммы частот, превышающей половину. В нашем примере сумма частот составила ее половина - 20.
Накопленная сумма частот ряда получилась равной Варианта, соответствующая этой сумме, т.е. 1600 руб., и есть медиана ряда.
Если же сумма накопленных частот против одной из вариант равна точно половине сумме частот, то медиана определяется как средняя арифметическая этой варианты и последующей.
Медиана интервального вариационного ряда распределения определяется по формуле
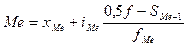
где  — начальное значение интервала, содержащего медиану;
— начальное значение интервала, содержащего медиану;
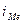 — величина медианного интервала;
— величина медианного интервала;
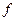 — сумма частот ряда;
— сумма частот ряда;
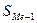 — сумма накопленных частот, предшествующих медианному интервалу;
— сумма накопленных частот, предшествующих медианному интервалу;
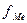 — частота медианного интервала.
— частота медианного интервала.
Квартили и децили
Более общая постановка вариант, занимающих определенное порядковое место в ранжированном ряду, называется порядковой статистикой. Различают порядковые статистики, отсекающие четверти совокупности, которые называются квартили;в первую или нижнюю (отсекающие четверть совокупности снизу), третью или верхнюю (отсекающие четверть сверху). Второй квартиль можно назвать медиану. Далее можно говорить об отсекающих десятые части — децилях и т.д.
Определение этих порядковых статистик в вариационном ряду, так же как и определение медианы, начинается с расчета порядкового номера соответствующего варианта, а затем по накопленным частотам определяется интервал, в котором находится соответствующий вариант. Определение величины накопленного варианта внутри интервала тоже абсолютно аналогично нахождению медианы.
В интервальном вариационном ряду квартили внутри определенного по накопленным частотам интервала рассчитываются по следующим формулам: 1
Нижний квартиль
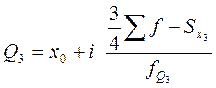
Верхний квартиль
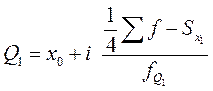 , где
, где
х0 — нижняя граница квартальных интервалов;
i — величина интервала;
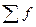 — сумма частот;
— сумма частот;
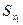 — накопленная частота интервала, предшествующего нижнему квартилю;
— накопленная частота интервала, предшествующего нижнему квартилю;
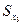 — накопленная частота интервала, предшествующего верхнему квартилю;
— накопленная частота интервала, предшествующего верхнему квартилю;
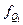 - частота квартального интервала.
- частота квартального интервала.
Формулы для децилей в интервальном вариационном ряду записываются следующим образом:
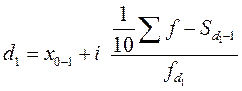
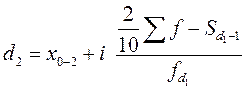
и т.д.
Вопросы для самоконтроля
1. Что такое средние величины и каковы их роль и значение?
2. Какие существуют средние величины и как рассчитываются средняя арифметическая простая и взвешенная?
3. Как осуществляется расчет средней арифметической по данным интервального ряда?
4. Свойства средней арифметической.
5. Средняя хронологическая для интервального и моментного ряда.
6. Что такое средняя гармоническая и как рассчитать среднюю гармоническую простую и взвешенную?
7. В чем сущность моды и как она рассчитывается для вариационного и интервального ряда?
8. Что такое медиана, какими свойствами она обладает и как рассчитывается медиана для интервального ряда?
9. Квартили и децили. Для каких целей они применяются и как они рассчитываются?
Дата добавления: 2017-04-20; просмотров: 1013;
