Тангенциальная составляющая ускорения 1 страница

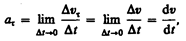
т. е. равна первой производной по времени от модуля скорости, определяя тем самым быстроту изменения скорости по модулю.

Найдем вторую составляющую ускорения. Допустим, что точка В достаточно близка к точке А, поэтому Ds можно считать дугой окружности некоторого радиуса r, мало отличающейся от хорды АВ. Тогда из подобия треугольников АОВ и EAD следует Dv_n/AB = v₁/r, но так как AB = vDt, то

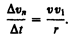
В пределе при 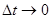получим .

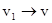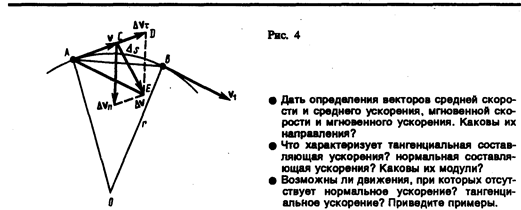
Поскольку 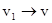, угол EAD стремится к нулю, а так как треугольник EAD равнобед­ренный, то угол ADE между v и Dv_n стремится к прямому. Следовательно, при 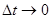векторы Dv_n и v оказываются взаимно перпендикулярными. Tax как вектор скорости направлен по касательной к траектории, то вектор Dv_n, перпендикулярный вектору скорости, направлен к центру ее кривизны. Вторая составляющая ускорения, равная

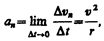
называется нормальной составляющей ускорения и направлена по нормали к траектории к центру ее кривизны (поэтому ее называют также центростремительным ускорением).

Полное ускорение тела есть геометрическая сумма тангенциальной и нормальной составляющих (рис.5):

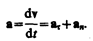
Итак, тангенциальная составляющая ускорения характеризует быстроту изменения скорости по модулю (направлена по касательной к траектории), а нормальная состав­ляющая ускорения — быстроту изменения скорости по направлению (направлена к цен­тру кривизны траектории).

В зависимости от тангенциальной и нормальной составляющих ускорения движе­ние можно классифицировать следующим образом:

1) 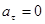, а_n = 0 — прямолинейное равномерное движение;

2) 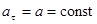, а_n = 0 — прямолинейное равнопеременное движение. При таком виде движения

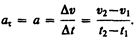
Если начальный момент времени t₁=0, а начальная скорость v₁=v₀, то, обозначив t₂=t и v₂=v, получим 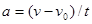, откуда

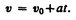
Проинтегрировав эту формулу в пределах от нуля до произвольного момента времени t, найдем, что длина пути, пройденного точкой, в случае равнопеременного движения

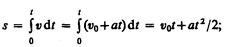
3) 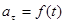, а_n = 0— прямолинейное движение с переменным ускорением;

4) 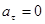, а_n = const. При 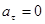скорость по модулю не изменяется, а изменяется по направлению. Из формулы a_n=v²/r следует, что радиус кривизны должен быть посто­янным. Следовательно, движение по окружности является равномерным;

5) 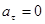, 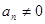— равномерное криволинейное движение;

6) 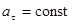, 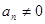— криволинейное равнопеременное движение;

7) 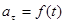, 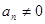— криволинейное движение с переменным ускорением.

§ 4. Угловая скорость и угловое ускорение

Рассмотрим твердое тело, которое вращается вокруг неподвижной оси. Тогда отдель­ные точки этого тела будут описывать окружности разных радиусов, центры которых лежат на оси вращения. Пусть некоторая точка движется по окружности радиуса R (рис. 6). Ее положение через промежуток времени Dt зададим углом D 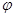. Элементар­ные (бесконечно малые) повороты можно рассматривать как векторы (они обозначают­ся 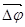или ). 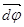Модуль вектора 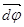равен углу поворота, а его направление совпадает с направлением поступательного движения острия винта, головка которого вращается в направлении движения точки по окружности, т.е. подчиняетсяправилу правого винта(рис.6). Векторы, направления которых связываются с направлением вращения, назы­ваютсяпсевдовекторами илиаксиальными векторами. Эти векторы не имеют опреде­ленных точек приложения: они могут откладываться из любой точки оси вращения.

Угловой скоростью называется векторная величина, равная первой производной угла поворота тела по времени:

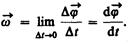
Вектор 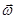направлен вдоль оси вращения по правилу правого винта, т.е. так же, как и вектор 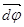(рис.7). Размерность угловой скорости dim w=T^–1, а ее единица — ради­ан в секунду (рад/с).

Линейная скорость точки (см. рис. 6)

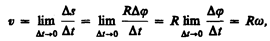
т. е.

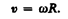
В векторном виде формулу для линейной скорости можно написать как векторное произведение:

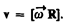
При этом модуль векторного произведения, по определению, равен 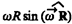, а направление совпадает с направлением поступательного движения правого винта при его вращении от 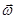к R.

Если ( 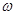= const, то вращение равномерное и его можно характеризовать периодом вращения T — временем, за которое точка совершает один полный оборот, т.е. поворачивается на угол 2p. Так как промежутку времени Dt = T соответствует 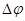= 2p, то 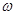= 2p/T, откуда

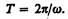
Число полных оборотов, совершаемых телом при равномерном его движении по окружности, в единицу времени называется частотой вращения:

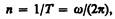
откуда

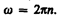
Угловым ускорением называется векторная величина, равная первой производной угловой скорости по времени:

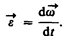
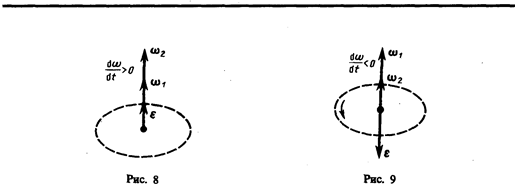
При вращении тела вокруг неподвижной оси вектор углового ускорения направлен вдоль оси вращения в сторону вектора элементарного приращения угловой скорости. При ускоренном движении вектор 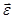сонаправлен вектору 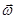(рис.8), при замедлен­ном — противонаправлен ему (рис.9).

Тангенциальная составляющая ускорения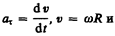

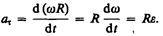
Нормальная составляющая ускорения

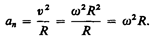
Таким образом, связь между линейными (длина пути s, пройденного точкой по дуге окружности радиуса R, линейная скорость v, тангенциальное ускорение 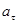, нормальное ускорение 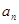) и угловыми величинами (угол поворота j, угловая скорость w, угловое ускорение e) выражается следующими формулами:

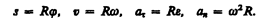
В случае равнопеременного движения точки по окружности (e=const)

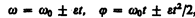
где w₀ — начальная угловая скорость.

Задачи

1.1. Зависимость пройденного телом пути от времени задается уравнением s=A+Bt+Ct²+Dt³(С=0,1 м/с², D=0,03 м/с³). Определить: 1) время после начала движения, через которое ускорение а тела будет равно 2 м/с²; 2) среднее ускорение áаñ тела за этот промежу­ток времени. [1) 10 с; 2) 1,1 м/с²]

1.2. Пренебрегая сопротивлением воздуха, определить угол, под которым тело брошено к гори­зонту, если максимальная высота подъема тела равна 1/4 дальности его полета. [45°]

1.3. Колесо радиусом R=0,1 м вращается так, что зависимость угловой скорости от времени задается уравнением w = 2At + 5Bt⁴(A = 2 рад/с² и B = 1 рад/с⁵). Определить полное ускорение точек обода колеса через t=1 с после начала вращения и число оборотов, сделан­ных колесом за это время. [а=8,5 м/с²; N=0,48]

1.4. Нормальное ускорение точки, движущейся по окружности радиусом r=4 м, задается уравне­нием a_n=A+Bt+Ct²(А=1 м/с², B=6 м/с³, С=3 м/с⁴). Определить: 1) тангенциальное ускорение точки; 2) путь, пройденный точкой за время t₁= 5 с после начала движения; 3) полное ускорение для момента времени t₂=1 с. [1) 6 м/с²; 2) 85 м; 3) 6,32 м/с²]

1.5. Частота вращения колеса при равнозамедленном движении за t=1 мин уменьшилась от 300 до 180 мин^–1. Определить: 1) угловое ускорение колеса; 2) число полных оборотов, сделанных колесом за это время. [1) 0,21 рад/с²; 2) 240]

1.6. Диск радиусом R=10 см вращается вокруг неподвижной оси так, что зависимость угла поворота радиуса диска от времени задается уравнением j=A+Bt+Ct²+Dt³ (B=1 рад/с, С=1 рад/с², D=1 рад/с³). Определить для точек на ободе колеса к концу второй секунды после начала движения: 1) тангенциальное ускорение 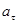; 2) нормальное ускорение а_n; 3) полное ускорение а. [1) 1,4 м/с²; 2) 28,9 м/с²; 3) 28,9 м/с²]

Глава 2 Динамика материальной точки и поступательного движения твердого тела

§ 5. Первый закон Ньютона. Масса. Сила

Динамика является основным разделом механики, в ее основе лежат три закона Ньютона, сформулированные им в 1687 г. Законы Ньютона играют исключительную роль в механике и являются (как и все физические законы) обобщением результатов огромного человеческого опыта. Их рассматривают как систему взаимосвязанных законов и опытной проверке подвергают не каждый отдельный закон, а всю систему в целом.

Первый закон Ньютона: всякая материальная точка (тело) сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока воздействие со стороны других тел не заставит ее изменить это состояние. Стремление тела сохранять состояние покоя или равномерного прямолинейного движения называется инертностью. Поэтому первый закон Ньютона называют также законом инерции.

Механическое движение относительно, и его характер зависит от системы отсчета. Первый закон Ньютона выполняется не во всякой системе отсчета, а те системы, по отношению к которым он выполняется, называются инерциальными системами отсчета. Инерциальной системой отсчета является такая система отсчета, относительно которой материальная точка, свободная от внешних воздействий, либо покоится, либо движется равномерно и прямолинейно. Первый закон Ньютона утверждает существование инерциальных систем отсчета.

Опытным путем установлено, что инерциальной можно считать гелиоцентрическую (звездную) систему отсчета (начало координат находится в центре Солнца, а оси проведаны в направлении определенных звезд). Система отсчета, связанная с Землей, строго говоря, неинерциальна, однако эффекты, обусловленные ее неинерциальностью (Земля вращается вокруг собственной оси и вокруг Солнца), при решении многих задач пренебрежимо малы, и в этих случаях ее можно считать инерциальной.

Из опыта известно, что при одинаковых воздействиях различные тела неодинаково изменяют скорость своего движения, т.е., иными словами, приобретают различные ускорения. Ускорение зависит не только от величины воздействия, но и от свойств самого тела (от его массы).

Масса тела — физическая величина, являющаяся одной из основных характеристик материи, определяющая ее инерционные (инертная масса) и гравитационные (гравитационная масса) свойства. В настоящее время можно считать доказанным, что инертная и гравитационная массы равны друг другу (с точностью, не меньшей 10^–12 их значения).

Чтобы описывать воздействия, упоминаемые в первом законе Ньютона, вводят понятие силы. Под действием сил тела либо изменяют скорость движения, т. е. приобретают ускорения (динамическое проявление сил), либо деформируются, т. е. изменяют свою форму и размеры (статическое проявление сил). В каждый момент времени сила характеризуется числовым значением, направлением в пространстве и точкой приложения. Итак, сила— это векторная величина, являющаяся мерой механического воздействия на тело со стороны других тел или полей, в результате которого тело приобретает ускорение или изменяет свою форму и размеры.

§ 6. Второй закон Ньютона

Второй закон Ньютона — основной закон динамики поступательного движения — от­вечает на вопрос, как изменяется механическое движение материальной точки (тела) под действием приложенных к ней сил.

Если рассмотреть действие различных сил на одно и то же тело, то оказывается, что ускорение, приобретаемое телом, всегда прямо пропорционально равнодействующей приложенных сил:

а ~ F (т = const). (6.1)

При действии одной и той же силы на тела с разными массами их ускорения оказываются различными, а именно

а ~ 1/т (F = const). (6.2)

Используя выражения (6.1) и (6.2) и учитывая, что сила и ускорение—величины векторные, можем записать

а = kF/m. (6.3)

Соотношение (6.3) выражает второй закон Ньютона: ускорение, приобретаемое материальной точкой (телом), пропорционально вызывающей его силе, совпадает с нею по направлению и обратно пропорционально массе материальной точки (тела).

В СИ коэффициент пропорциональности k= 1. Тогда

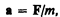
или

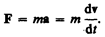(6.4)

Учитывая, что масса материальной точки (тела) в классической механике есть величина постоянная, в выражении (6.4) ее можно внести под знак производной:

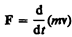(6.5)

Векторная величина

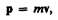(6.6)

численно равная произведению массы материальной точки на ее скорость и имеющая направление скорости, называется импульсом (количеством движения) этой материаль­ной точки.

Подставляя (6.6) в (6.5), получим

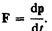(6.7)

Это выражение — более общая формулировка второго закона Ньютона: скорость изме­нения импульса материальной точки равна действующей на нее силе. Выражение (6.7) называется уравнением движения материальной точки.

Единица силы в СИ — ньютон (Н): 1 Н — сила, которая массе 1 кг сообщает ускорение 1 м/с² в направлении действия силы:

1 Н = 1 кг×м/с².

Второй закон Ньютона справедлив только в инерциальных системах отсчета. Первый закон Ньютона можно получить из второго. Действительно, в случае равенст­ва нулю равнодействующей сил (при отсутствии воздействия на тело со стороны других тел) ускорение (см. (6.3)) также равно нулю. Однако первый закон Ньютона рассматривается как самостоятельный закон (а не как следствие второго закона), так как именно он утверждает существование инерциальных систем отсчета, в которых только и выполняется уравнение (6.7).

В механике большое значение имеет принцип независимости действия сил: если на материальную точку действует одновременно несколько сил, то каждая из этих сил сообщает материальной точке ускорение согласно второму закону Ньютона, как будто других сил не было. Согласно этому принципу, силы и ускорения можно разлагать на составляющие, использование которых приводит к существенному упрощению решения задач. Например, на рис. 10 действующая сила F=ma разложена на два компонен­та: тангенциальную силу F_t, (направлена по касательной к траектории) и нормальную силу F_n (направлена по нормали к центру кривизны). Используя выражения 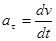и 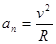, а также 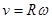, можно записать:

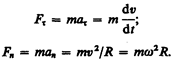
Если на материальную точку действует одновременно несколько сил, то, согласно принципу независимости действия сил, под F во втором законе Ньютона понимают результирующую силу.

§ 7. Третий закон Ньютона

Взаимодействие между материальными точками (телами) определяется третьим зако­ном Ньютона: всякое действие материальных точек (тел) друг на друга носит характер взаимодействия; силы, с которыми действуют друг на друга материальные точки, всегда равны по модулю, противоположно направлены и действуют вдоль прямой, соединяющей эти точки:

F₁₂ = – F₂₁, (7.1)

где F₁₂ — сила, действующая на первую материальную точку со стороны второй;

F₂₁ — сила, действующая на вторую материальную точку со стороны первой. Эти силы приложены к разным материальным точкам (телам), всегда действуют парами и явля­ются силами одной природы.

Третий закон Ньютона позволяет осуществить переход от динамики отдельной материальной точки к динамике системы материальных точек. Это следует из того, что и для системы материальных точек взаимодействие сводится к силам парного взаимодействия между материальными точками.

§ 8. Силы трения

Обсуждая до сих пор силы, мы не интересовались их происхождением. Однако в меха­нике мы будем рассматривать различные силы: трения, упругости, тяготения.

Из опыта известно, что всякое тело, движущееся по горизонтальной поверхности другого тела, при отсутствии действия на него других сил с течением времени замедля­ет свое движение и в конце концов останавливается. Это можно объяснить существова­нием силы трения, которая препятствует скольжению соприкасающихся тел друг относительно друга. Силы трения зависят от относительных скоростей тел. Силы трения могут быть разной природы, но в результате их действия механическая энергия всегда превращается во внутреннюю энергию соприкасающихся тел.

Различают внешнее (сухое) и внутреннее (жидкое или вязкое) трение. Внешним трением называется трение, возникающее в плоскости касания двух соприкасающихся тел при их относительном перемещении. Если соприкасающиеся тела неподвижны друг относительно друга, говорят о трении покоя, если же происходит относительное перемещение этих тел, то в зависимости от характера их относительного движения говорят о трении скольжения, качения или верчения.

Внутренним трением называется трение между частями одного и того же тела, например между различными слоями жидкости или газа, скорости которых меняются от слоя к слою. В отличие от внешнего трения здесь отсутствует трение покоя. Если тела скользят относительно друг друга и разделены прослойкой вязкой жидкости (смазки), то трение происходит в слое смазки. В таком случае говорят о гидродинамическом трении (слой смазки достаточно толстый) и граничном трении (толщина смазоч­ной прослойки »0,1 мкм и меньше).

Обсудим некоторые закономерности внешнего трения. Это трение обусловлено шероховатостью соприкасающихся поверхностей; в случае же очень гладких поверх­ностей трение обусловлено силами межмолекулярного притяжения.

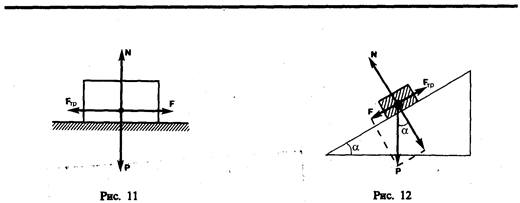
Рассмотрим лежащее на плоскости тело (рис. 11), к которому приложена горизон­тальная сила F. Тело придет в движение лишь тогда, когда приложенная сила F будет больше силы трения F_тр. Французские физики Г. Амонтон (1663—1705) и Ш. Кулон (1736—1806) опытным путем установили следующий закон: сила трения скольжения F_тр пропорциональна силе N нормального давления, с которой одно тело действует на другое:

F_тр = f N,

где f — коэффициент трения скольжения, зависящий от свойств соприкасающихся поверхностей.

Найдем значение коэффициента трения. Если тело находится на наклонной плоско­сти с углом наклона a (рис.12), то оно приходит в движение, только когда тангенциаль­ная составляющая F силы тяжести Р больше силы трения F_тр. Следовательно, в пре­дельном случае (начало скольжения тела) F=F_тр. или Psin a₀ = f N = f P cos a₀,откуда

f = tga₀.

Таким образом, коэффициент трения равен тангенсу угла a₀, при котором начинается скольжение тела по наклонной плоскости.

Для гладких поверхностей определенную роль начинает играть межмолекулярное притяжение. Для них применяется закон трения скольжения

F_тр = f _ист (N + Sp₀),

где р₀ — добавочное давление, обусловленное силами межмолекулярного притяжения, которые быстро уменьшаются с увеличением расстояния между частицами; S — пло­щадь контакта между телами; f_ист — истинный коэффициент трения скольжения.

Трение играет большую роль в природе и технике. Благодаря трению движется транспорт, удерживается забитый в стену гвоздь и т. д.

В некоторых случаях силы трения оказывают вредное действие и поэтому их надо уменьшать. Для этого на трущиеся поверхности наносят смазку (сила трения уменьша­ется примерно в 10 раз), которая заполняет неровности между этими поверхностями и располагается тонким слоем между ними так, что поверхности как бы перестают касаться друг друга, а скользят друг относительно друга отдельные слои жидкости. Таким образом, внешнее трение твердых тел заменяется значительно меньшим внут­ренним трением жидкости.

Радикальным способом уменьшения силы трения является замена трения скольже­ния трением качения (шариковые и роликовые подшипники и т. д.). Сила трения качения определяется по закону, установленному Кулоном:

F_тр=f_к N/r, (8.1)

где r — радиус катящегося тела; f_к — коэффициент трения качения, имеющий размер­ность dim f_к =L. Из (8.1) следует, что сила трения качения обратно пропорциональна радиусу катящегося тела.

§ 9. Закон сохранения импульса. Центр масс

Для вывода закона сохранения импульса рассмотрим некоторые понятия. Совокуп­ность материальных точек (тел), рассматриваемых как единое целое, называется механической системой. Силы взаимодействия между материальными точками механичес­кой системы называются — внутренними. Силы, с которыми на материальные точки системы действуют внешние тела, называются внешними. Механическая система тел, на которую не действуют внешние силы, называется замкнутой (или изолированной). Если мы имеем механическую систему, состоящую из многих тел, то, согласно третьему закону Ньютона, силы, действующие между этими телами, будут равны и проти­воположно направлены, т. е. геометрическая сумма внутренних сил равна нулю.

Рассмотрим механическую систему, состоящую из n тел, масса и скорость которых соответственно равны m₁, m₂,.... m_n, и v₁, v₂,..., v_n. Пусть 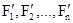— равнодейст­вующие внутренних сил, действующих на каждое из этих тел, a 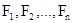— равно­действующие внешних сил. Запишем второй закон Ньютона для каждого из n тел механической системы:

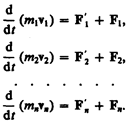
Складывая почленно эти уравнения, получаем

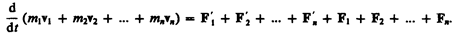
Но так как геометрическая сумма внутренних сил механической системы по третьему закону Ньютона равна нулю, то

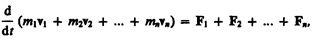
или

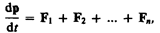(9.1)

где 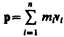— импульс системы. Таким образом, производная по времени от им­пульса механической системы равна геометрической сумме внешних сил, действующих на систему.

В случае отсутствия внешних сил (рассматриваем замкнутую систему)

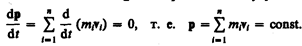
Последнее выражение и является законом сохранения импульса: импульс замкнутой системы сохраняется, т. е. не изменяется с течением времени.

Закон сохранения импульса справедлив не только в классической физике, хотя он и получен как следствие законов Ньютона. Эксперименты доказывают, что он выпол­няется и для замкнутых систем микрочастиц (они подчиняются законам квантовой механики). Этот закон носит универсальный характер, т. е. закон сохранения импуль­са — фундаментальный закон природы.