Предмет физики и ее связь с другими науками

Окружающий вас мир, все существующее вокруг вас и обнаруживаемое нами посред­ством ощущений представляет собой материю.

Неотъемлемым свойством материи и формой ее существования является движение. Движение в широком смысле слова — это всевозможные изменения материи — от простого перемещения до сложнейших процессов мышления.

Разнообразные формы движения материи изучаются различными науками, в том числе и физикой. Предмет физики, как, впрочем, и любой науки, может быть раскрыт только по мере его детального изложения. Дать строгое определение предмета физики довольно сложно, потому что границы между физикой и рядом смежных дисциплин условны. На данной стадии развития нельзя сохранить определение физики только как науки о природе.

Академик А. Ф. Иоффе (1880—1960; российский физик)* определил физику как науку, изучающую общие свойства и законы движения вещества и поля. В настоящее время общепризнано, что вес взаимодействия осуществляются посредством полей, например гравитационных, электромагнитных, полей ядерных сил. Поле наряду с ве­ществом является одной из форм существования материи. Неразрывная связь поля и вещества, а также различие в их свойствах будут рассмотрены по мере изучения курса.

*Все данные приведены по биографическому справочнику Ю. А. Храмова «Физики» (М.: Наука, 1983).

Физика — наука о наиболее простых и вместе с тем наиболее общих формах движения материи и их взаимных превращениях. Изучаемые физикой формы движения материи (механическая, тепловая и др.) присутствуют во всех высших и более сложных формах движения материи (химических, биологических и др.). Поэтому они, будучи наиболее простыми, являются в то же время наиболее общими формами движения материи. Высшие и более сложные формы движения материи — предмет изучения других наук (химии, биологии и др.).

Физика тесно связана с естественными науками. Эта теснейшая связь физики с другими отраслями естествознания, как отмечал академик С. И. Вавилов (1891—1955; российский физик и общественный деятель), привела к тому, что физика глубочайшими корнями вросла в астрономию, геологию, химию, биологию и другие естественные науки. В результате образовался ряд новых смежных дисциплин, таких, как астрофизика, биофизика и др.

Физика тесно связана и с техникой, причем эта связь имеет двусторонний характер. Физика выросла из потребностей техники (развитие механики у древних греков, например, было вызвано запросами строительной и военной техники того времени), и техника, в свою очередь, определяет направление физических исследований (напри­мер, в свое время задача создания наиболее экономичных тепловых двигателей вызвала бурное развитие термодинамики). С другой стороны, от развития физики зависит технический уровень производства. Физика — база для создания новых отраслей тех­ники (электронная техника, ядерная техника и др.).

Бурный темп развития физики, растущие связи ее с техникой указывают на значи­тельную роль курса физики во втузе: это фундаментальная база для теоретической подготовки инженера, без которой его успешная деятельность невозможна.

Единицы физических величин

Основным методом исследования в физике является опит — основанное на практике чувственно-эмпирическое познание объективной действительности, т. е. наблюдение исследуемых явлений в точно учитываемых условиях, позволяющих следить за ходом явлений и многократно воспроизводить его при повторении этих условий.

Для объяснения экспериментальных фактов выдвигаются гипотезы. Гипотеза — это научное предположение, выдвигаемое для объяснения какого-либо явления и требующее проверки на опыте и теоретического обоснования для того, чтобы стать достоверной научной теорией.

В результате обобщения экспериментальных фактов, а также результатов деятель­ности людей устанавливаютсяфизические законы — устойчивые повторяющиеся объективные закономерности, существующие в природе. Наиболее важные законы устанавливают связь между физическими величинами, для чего необходимо эти вели­чины измерять. Измерение физической величины есть действие, выполняемое с помо­щью средств измерений для нахождения значения физической величины в принятых единицах. Единицы физических величин можно выбрать произвольно, но тогда возник­нут трудности при их сравнении. Поэтому целесообразно ввести систему единиц, охватывающую единицы всех физических величин.

Для построения системы единиц произвольно выбирают единицы для нескольких не зависящих друг от друга физических величии. Эти единицы называютсяосновными.Остальные же величины и их единицы выводятся из законов, связывающих эти величины и их единицы с основными. Они называютсяпроизводными.

В настоящее время обязательна к применению в научной, а также в учебной литературе Система Интернациональная (СИ), которая строится на семи основных единицах — метр, килограмм, секунда, ампер, кельвин, моль, кандела — и двух допол­нительных — радиан и стерадиан.

Метр (м) — длина пути, проходимого светом в вакууме за 1/299792458 с.

Килограмм (кг) — масса, равная массе международного прототипа килограмма (платиноиридиевого цилиндра, хранящегося в Международном бюро мер и весов в Севре, близ Парижа).

Секунда (с) — время, равное 9192631770 периодам излучения, соответствующего переходу между двумя сверхтонкими уровнями основного состояния атома цезия-133.

Ампер (А) — сила неизменяющегося тока, который при прохождении по двум параллельным прямолинейным проводникам бесконечной длины и ничтожно малого поперечного сечения, расположенным в вакууме на расстоянии 1 м один от другого, создаст между этими проводниками силу, равную 2×10^–7 Н на каждый метр длины.

Кельвин (К) — 1/273,16 часть термодинамической температуры тройной точки воды.

Моль (моль) — количество вещества системы, содержащей столько же структур­ных элементов, сколько атомов содержится в нуклиде ¹²С массой 0,012 кг.

Кандела (кд) — сила света в заданном направлении источника, испускающего монохроматическое излучение частотой 540×10¹² Гц, энергетическая сила света кото­рого в этом направлении составляет 1/683 Вт/ср.

Радиан (рад) — угол между двумя радиусами окружности, длина дуги между которыми равна радиусу.

Стерадиан (ср) — телесный угол с вершиной в центре сферы, вырезающий на поверхности сферы площадь, равную площади квадрата со стороной, равной радиусу сферы.

Для установления производных единиц используют физические законы, связыва­ющие их с основными единицами. Например, из формулы равномерного прямолиней­ного движения v=s/t (s – пройденный путь, t — время) производная единица скорости получается равной 1 м/с.

1 ФИЗИЧЕСКИЕ ОСНОВЫ МЕХАНИКИ

Глава 1Элементы кинематики

§ 1. Модели в механике. Система отсчета. Траектория, длина пути, вектор перемещения

Механика — часть физики, которая изучает закономерности механического движения и причины, вызывающие или изменяющие это движение.Механическое движе­ние — это изменение с течением времени взаимного расположения тел или их частей.

Развитие механики как науки начинается с III в. до н. э., когда древнегреческий ученый Архимед (287—212 до н. э.) сформулировал закон равновесия рычага и законы равновесия плавающих тел. Основные законы механики установлены итальянским физиком и астрономом Г. Галилеем (1564—1642) н окончательно сформулированы английским ученым И. Ньютоном (1643—1727).

Механика Галилея—Ньютона называетсяклассической механикой. В ней изучаются законы движения макроскопических тел, скорости которых малы по сравнению со скоростью света с в вакууме. Законы движения макроскопических тел со скоростями, сравнимыми со скоростью с, изучаютсярелятивистской механикой, основанной на специальной теории относительности, сформулированной А. Эйнштейном (1879—1955). Для описания движения микроскопических тел (отдельные атомы и элементарные частицы) законы классической механики неприменимы — они заменяются законами китовой механики.

В первой части нашего курса мы будем изучать механику Галилея—Ньютона, т.е. рассматривать движение макроскопических тел со скоростями, значительно меньшими скорости с. В классической механике общепринята концепция пространства и времени, разработанная И. Ньютоном и господствовавшая в естествознании на протяжении XVII—XIX вв. Механика Галилея—Ньютона рассматривает пространство и время как объективные формы существования материи, но в отрыве друг от друга и от движения материальных тел, что соответствовало уровню знаний того времени.

Механика делится на три раздела: I) кинематику; 2) динамику; 3) статику.

Кинематика изучает движение тел, не рассматривая причины, которые это движение обусловливают.

Динамика изучает законы движения тел и причины, которые вызывают или изменя­ют это движение.

Статика изучает законы равновесия системы тел. Если известны законы движения тел, то из них можно установить и законы равновесия. Поэтому законы статики отдельно от законов динамики физика не рассматривает.

Механика для описания движения тел в зависимости от условий конкретных задач использует разные физические модели. Простейшей моделью являетсяматериальная точка — тело, обладающее массой, размерами которого в данной задаче можно пренебречь. Понятие материальной точки — абстрактное, но его введение облегчает решение практических задач. Например, изучая движение планет по орбитам вокруг Солнца, можно принять их за материальные точки.

Произвольное макроскопическое тело или систему тел можно мысленно разбить на малые взаимодействующие между собой части, каждая из которых рассматривается как материальная точка. Тогда изучение движения произвольной системы тел сводится к изучению системы материальных точек. В механике сначала изучают движение одной материальной точки, а затем переходят к изучению движения системы материальных точек.

Под воздействием тел друг на друга тела могут деформироваться, т. е. изменять свою форму и размеры. Поэтому в механике вводится еще одна модель — абсолютно твердое тело. Абсолютно твердым телом называется тело, которое ни при каких условиях не может деформироваться и при всех условиях расстояние между двумя точками (или точнее между двумя частицами) этого тела остается постоянным.

Любое движение твердого тела можно представить как комбинацию поступатель­ного и вращательного движений. Поступательное движение — это движение, при кото­ром любая прямая, жестко связанная с движущимся телом, остается параллельной своему первоначальному положению. Вращательное движение — это движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной и той же прямой, называемой осью вращения.

Движение тел происходит в пространстве и во времени. Поэтому для описания движения материальной точки надо знать, в каких местах пространства эта точка находилась и в какие моменты времени она проходила то или иное положение.

Положение материальной точки определяется по отношению к какому-либо друго­му, произвольно выбранному телу, называемому телом отсчета. С ним связывается система отсчета — совокупность системы координат и часов, связанных с телом от­счета. В декартовой системе координат, используемой наиболее часто, положение точки А в данный момент времени по отношению к этой системе характеризуется тремя координатами x, y и z или радиусом-вектором r, проведенным из начала системы координат в данную точку (рис. 1).

При движении материальной точки ее координаты с течением времени изменяются. В общем случае ее движение определяется скалярными уравнениями

x = x(t), у = y(t), z = z(t), (1.1)

эквивалентными векторному уравнению

r = r(t). (1.2)

Уравнения (1.1) и соответственно (1.2) называютсякинематическими уравнениями дви­женияматериальной точки.

Число независимых координат, полностью определяющих положение точки в про­странстве, называется числом степеней свободы. Если материальная точка свободно движется в пространстве, то, как уже было сказано, она обладает тремя степенями свободы (координаты х, у и z), если она движется по некоторой поверхности, то двумя степенями свободы, если вдоль некоторой линии, то одной степенью свободы.

Исключая t в уравнениях (1.1) и (1.2), получим уравнение траектории движения материальной точки. Траектория движения материальной точки — линия, описыва­емая этой точкой в пространстве. В зависимости от формы траектории движение может быть прямолинейным или криволинейным.

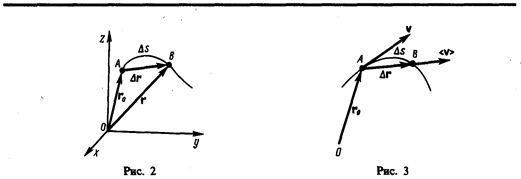
Рассмотрим движение материальной точки вдоль произвольной траектории (рис. 2). Отсчет времени начнем с момента, когда точка находилась в положении А. Длина участка траектории АВ, пройденного материальной точкой с момента начала отсчета времени, называется длиной пути Ds и является скалярной функцией времени: Ds = Ds(t). Вектор Dr = r —r₀, проведенный из начального положения движущейся точки в положение ее в данный момент времени (приращение радиуса-вектора точки за рассматриваемый промежуток времени), называется перемещением.

При прямолинейном движении вектор перемещения совпадает с соответствующим участком траектории и модуль перемещения |Dr| равен пройденному пути Ds.

§ 2. Скорость

Для характеристики движения материальной точки вводится векторная величина — скорость, которой определяется как быстрота движения, так и его направ­ление в данный момент времени.

Пусть материальная точка движется по какой-либо криволинейной траектории так, что в момент времени t ей соответствует радиус-вектор r₀ (рис. 3). В течение малого промежутка времени Dt точка пройдет путь Ds и получит элементарное (бесконечно малое) перемещение Dr.

Вектором средней скорости <v> называется отношение приращения Dr радиу­са-вектора точки к промежутку времени Dt:

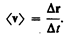(2.1)

Направление вектора средней скорости совпадает с направлением Dr. При неог­раниченном уменьшении Dt средняя скорость стремится к предельному значению, которое называетсямгновенной скоростью v:

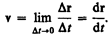
Мгновенная скорость v, таким образом, есть векторная величина, равная первой производной радиуса-вектора движущейся точки по времени. Так как секущая в пре­деле совпадает с касательной, то вектор скорости v направлен по касательной к траек­тории в сторону движения (рис. 3). По мере уменьшения Dt путь Ds все больше будет приближаться к |Dr|, поэтому модуль мгновенной скорости

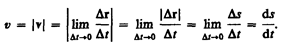
Таким образом, модуль мгновенной скорости равен первой производной пути по времени:

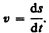(2.2)

Принеравномерном движении — модуль мгновенной скорости с течением времени изменяется. В данном случае пользуются скалярной величиной ávñ —средней скоро­стью неравномерного движения:

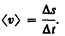
Из рис. 3 вытекает, что ávñ> |ávñ|, так как Ds > |Dr|, и только в случае прямолиней­ного движения

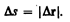
Если выражение ds = vdt (см. формулу (2.2)) проинтегрировать по времени в пре­делах от t до t + Dt, то найдем длину пути, пройденного точкой за время Dt:

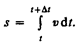(2.3)

В случаеравномерного движения числовое значение мгновенной скорости постоянно; тогда выражение (2.3) примет вид

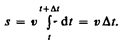
Длина пути, пройденного точкой за промежуток времени от t₁ до t₂, дается интегралом

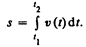
§ 3. Ускорение и его составляющие

В случае неравномерного движения важно знать, как быстро изменяется скорость с течением времени. Физической величиной, характеризующей быстроту изменения скорости по модулю и направлению, является ускорение.

Рассмотримплоское движение, т.е. движение, при котором все участки траектории точки лежат в одной плоскости. Пусть вектор v задает скорость точки А в момент времени t. За время Dt движущаяся точка перешла в положение В и приобрела скорость, отличную от v как по модулю, так и направлению и равную v₁ = v + Dv. Перенесем вектор v₁ в точку А и найдем Dv (рис. 4).

Средним ускорением неравномерного движения в интервале от t до t + Dt называется векторная величина, равная отношению изменения скорости Dv к интервалу вре­мени Dt

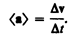
Мгновенным ускорением а (ускорением) материальной точки в момент време­ни t будет предел среднего ускорения:

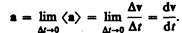
Таким образом, ускорение a есть векторная величина, равная первой производной скорости по времени.

Разложим вектор Dv на две составляющие. Для этого из точки А (рис. 4) по направлению скорости v отложим вектор 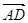, по модулю равный v₁. Очевидно, что вектор 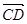, равный 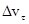, определяет изменение скорости за время Dt по моду­лю: 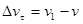. Вторая же составляющая 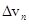вектора Dv характеризует изменение ско­рости за время Dt по направлению.