Тангенциальная составляющая ускорения 6 страница
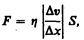 (31.1)
(31.1)
где коэффициент пропорциональности m, зависящий от природы жидкости, называется динамической вязкостью (или просто вязкостью).
Единица вязкости — паскаль-секунда (Па×с): 1 Па×с равен динамической вязкости среды, в которой при ламинарном течении и градиенте скорости с модулем, равным 1 м/с на 1 м, возникает сила внутреннего трения 1 Н на 1 м2 поверхности касания слоев (1 Па×с= 1 Н×с/м2).
Чем больше вязкость, тем сильнее жидкость отличается от идеальной, тем большие силы внутреннего трения в ней возникают. Вязкость зависит от температуры, причем характер этой зависимости для жидкостей и газов различен (для жидкостей h с увеличением температуры уменьшается, у газов, наоборот, увеличивается), что указывает на различие в них механизмов внутреннего трения. Особенно сильно от температуры зависит вязкость масел. Например, вязкость касторового масла в интервале 18—40°С падает в четыре раза. Российский физик П. Л. Капица (1894—1984; Нобелевская премия 1978 г.) открыл, что при температуре 2,17 К жидкий гелий переходит в сверхтекучее состояние, в котором его вязкость равна нулю.
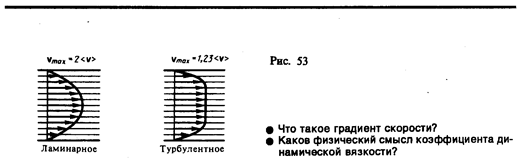
Существует два режима течения жидкостей. Течение называется ламинарным (слоистым), если вдоль потока каждый выделенный тонкий слой скользит относительно соседних, не перемешиваясь с ними, и турбулентным (вихревым), если вдоль потока происходит интенсивное вихреобразование и перемешивание жидкости (газа).
Ламинарное течение жидкости наблюдается при небольших скоростях ее движения. Внешний слой жидкости, примыкающий к поверхности трубы, в которой она течет, из-за сил молекулярного сцепления прилипает к ней и остается неподвижным. Скорости последующих слоев тем больше, чем больше их расстояние до поверхности трубы, и наибольшей скоростью обладает слой, движущийся вдоль оси трубы.
При турбулентном течении частицы жидкости приобретают составляющие скоростей, перпендикулярные течению, поэтому они могут переходить из одного слоя в другой. Скорость частиц жидкости быстро возрастает по мере удаления от поверхности трубы, затем изменяется довольно незначительно. Так как частицы жидкости переходят из одного слоя в другой, то их скорости в различных слоях мало отличаются. Из-за большого градиента скоростей у поверхности трубы обычно происходит образование вихрей.
Профиль усредненной скорости при турбулентном течении в трубах (рис. 53) отличается от параболического профиля при ламинарном течении более быстрым возрастанием скорости у стенок трубы и меньшей кривизной в центральной части течения. Характер течения зависит от безразмерной величины, называемойчислом Рейнольдса (О. Рейнольдс (1842—1912) — английский ученый):
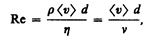
где n = h/p—кинематическая вязкость; р—плотность жидкости; <v>—средняя по сечению трубы скорость жидкости; d — характерный линейный размер, например диаметр трубы.
При малых значениях числа Рейнольдса 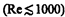 наблюдается ламинарное течение, переход от ламинарного течения к турбулентному происходит в области
наблюдается ламинарное течение, переход от ламинарного течения к турбулентному происходит в области 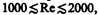 а при
а при 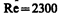 (для гладких труб) течение—турбулентное. Если число Рейнольдса одинаково, то режим течения различных жидкостей (газов) в трубах разных сечений одинаков.
(для гладких труб) течение—турбулентное. Если число Рейнольдса одинаково, то режим течения различных жидкостей (газов) в трубах разных сечений одинаков.
§ 32. Методы определения вязкости
1. Метод Стокса.* Этот метод определения вязкости основан на измерении скорости медленно движущихся в жидкости небольших тел сферической формы.
* Дж. Стокс (1819—1903) — английский физик и математик.
На шарик, падающий в жидкости вертикально вниз, действуют три силы: сила тяжести Р=4/3pr3rg (r — плотность шарика), сила Архимеда Р=4/3pr3r'g (r' — плотность жидкости) и сила сопротивления, эмпирически установленная Дж. Стоксом: F=6phrv, где r — радиус шарика, v — его скорость. При равномерном движении шарика
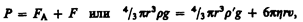
откуда
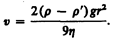
Измерив скорость равномерного движения шарика, можно определить вязкость жидкости (газа).
2. Метод Пуазейля.* Этот метод основан на ламинарном течении жидкости в тонком капилляре. Рассмотрим капилляр радиусом R и длиной l. В жидкости мысленно выделим цилиндрический слой радиусом r и толщиной dr (рис. 54). Сила внутреннего трения (см. (31.1)), действующая на боковую поверхность этого слоя,
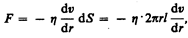
где dS — боковая поверхность цилиндрического слоя; знак минус означает, что при возрастании радиуса скорость уменьшается.
* Ж. Пуазейль (1799—1868) — французский физиолог и физик.
Для установившегося течения жидкости сила внутреннего трения, действующая на боковую поверхность цилиндра, уравновешивается силой давления, действующей на его основание:
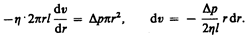
После интегрирования, полагая, что у стенок имеет место прилипание жидкости, т. е. скорость на расстоянии R от оси равна нулю, получаем
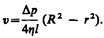
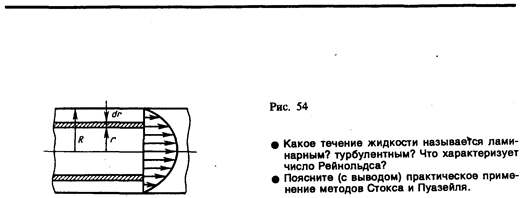
Отсюда видно, что скорости частиц жидкости распределяются по параболическому закону, причем вершина параболы лежит на оси трубы (см. также рис. 53).
За время t из трубы вытечет жидкость, объем которой
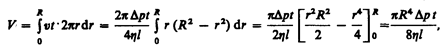
откуда вязкость
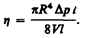
§ 33. Движение тел в жидкостях и газах
Одной из важнейших задач аэро- и гидродинамики является исследование движения твердых тел в газе и жидкости, в частности изучение тех сил, с которыми среда действует на движущееся тело. Эта проблема приобрела особенно большое значение в связи с бурным развитием авиации и увеличением скорости движения морских судов.
На тело, движущееся в жидкости или газе, действуют две силы (равнодействующую их обозначим R), одна из которых (Rx) направлена в сторону, противоположную движению тела (в сторону потока), —лобовое сопротивление, а вторая (Ry) перпендикулярна этому направлению —подъемная сила (рис. 55).
Если тело симметрично и его ось симметрии совпадает с направлением скорости, то на него действует только лобовое сопротивление, подъемная же сила в этом случае равна нулю. Можно доказать, что в идеальной жидкости равномерное движение происходит без лобового сопротивления. Если рассмотреть движение цилиндра в такой жидкости (рис. 56), то картина линий тока симметрична как относительно прямой, проходящей через точки А и В, так и относительно прямой, проходящей через точки С и D, т. с. результирующая сила давления на поверхность цилиндра будет равна нулю.

Иначе обстоит дело при движении тел в вязкой жидкости (особенно при увеличении скорости обтекания). Вследствие вязкости среды в области, прилегающей к поверхности тела, образуется пограничный слой частиц, движущихся с меньшими скоростями. В результате тормозящего действия этого слоя возникает вращение частиц и движение жидкости в пограничном слое становится вихревым. Если тело не имеет обтекаемой формы (нет плавно утончающейся хвостовой части), то пограничный слой жидкости отрывается от поверхности тела. За телом возникает течение жидкости (газа), направленное противоположно набегающему потоку. Оторвавшийся пограничный слой, следуя за этим течением, образует вихри, вращающиеся в противоположные стороны (рис. 57).
Лобовое сопротивление зависит от формы тела и его положения относительно потока, что учитывается безразмерным коэффициентом сопротивления Сx, определяемым экспериментально:
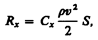 (33.1)
(33.1)
где r — плотность среды; v — скорость движения тела; S — наибольшее поперечное сечение тела.
Составляющую Rx можно значительно уменьшить, подобрав тело такой формы, которая не способствует образованию завихрения.
Подъемная сила может быть определена формулой, аналогичной (33.1):
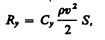
где Су — безразмерный коэффициент подъемной силы.
Для крыла самолета требуется большая подъемная сила при малом лобовом сопротивлении (это условие выполняется при малых углах атаки a (угол к потоку); см. рис. 55). Крыло тем лучше удовлетворяет этому условию, чем больше величина К=Су/Сx называемаякачеством крыла. Большие заслуги в конструировании требуемого профиля крыла и изучении влияния геометрической формы тела на коэффициент подъемной силы принадлежат «отцу русской авиации» Н. Е. Жуковскому (1847—1921).
Задачи
6.1. Полый железный шар (r =7,87 г/см3) весит в воздухе 5 Н, а в воде (r' = 1 г/см3) — 3 Н. Пренебрегая выталкивающей силой воздуха, определить объем внутренней полости шара. [139 см3]
6.2. Бак цилиндрической формы площадью основания S = 1 м2 и объемом V = 3 м3 заполнен водой. Пренебрегая вязкостью воды, определить время t, необходимое для опустошения бака, если на дне бака образовалось круглое отверстие площадью S1 =10 см2.
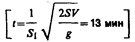
6.3. Сопло фонтана, дающего вертикальную струю высотой H = 5 м, имеет форму усеченного конуса, сужающегося вверх. Диаметр нижнего сечения d1 = 6 см, верхнего — d2 = 2 см. Высота сопла h = 1 м. Пренебрегая сопротивлением воздуха в струе и сопротивлением в сопле, определить: 1) расход воды в 1 с, подаваемой фонтаном; 2) разность Dр давления в нижнем сечении и атмосферного давления. Плотность воды r =1 г/см3. [1) 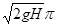 d2/4 = 3,1 х 10-3 м3/с; 2) Dp = pgh + pgH (1– d
d2/4 = 3,1 х 10-3 м3/с; 2) Dp = pgh + pgH (1– d 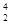 /d
/d 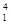 =58,3 кПа]
=58,3 кПа]
6.4. На горизонтальной поверхности стоит цилиндрический сосуд, в боковой поверхности которого имеется отверстие. Поперечное сечение отверстия значительно меньше поперечного сечения самого сосуда. Отверстие расположено на расстоянии h1 = 64 см ниже уровня воды в сосуде, который поддерживается постоянным, и на расстоянии h2 = 25 см от дна сосуда. Пренебрегая вязкостью воды, определить, на каком расстоянии по горизонтали от сосуда падает на поверхность струя, вытекающая из отверстия. [80 см]
6.5. В широком сосуде, наполненном глицерином (плотность r =1,2 г/см3), падает с установившейся скоростью 5 см/с стеклянный шарик (r' = 2,7 г/см3) диаметром 1 мм. Определить динамическую вязкость глицерина. [1,6 Па×с]
6.6. В боковую поверхность цилиндрического сосуда, установленного на столе, вставлен на высоте h1 = 5 см от его дна капилляр внутренним диаметром d = 2 мм и длиной l = 1 см. В сосуде поддерживается постоянный уровеньмашинного масла (плотность r = 0,9 г/см3 и динамическая вязкость h = 0,1 Па×с) на высоте h2 = 80 см выше капилляра. Определить, на каком расстоянии по горизонтали от конца капилляра падает на поверхность стола струя масла, вытекающая из отверстия. 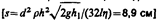
6.7. Определить наибольшую скорость, которую может приобрести свободно падающий в воздухе (r=1,29 г/см3) стальной шарик (r' = 9 г/см3) массой m = 20 г. Коэффициент Сх принять равным 0,5. [94 см/с]
Глава 7 Элементы специальной (частной) теории относительности
§ 34. Преобразования Галилея. Механический принцип относительности
В классической механике справедливмеханический принцип относительности (принцип относительности Галилея): законы динамики одинаковы во всех инерциальных системах отсчета.
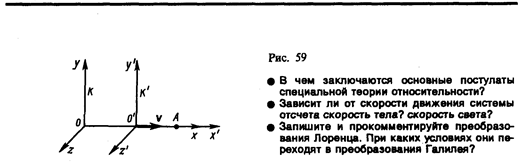
Для его доказательства рассмотрим две системы отсчета: инерциальную систему K (с координатами х, у, z), которую условно будем считать неподвижной, и систему K' (с координатами x', у', z'), движущуюся относительно K равномерно и прямолинейно со скоростью u (u=const). Отсчет времени начнем с момента, когда начала координат обеих систем совпадают. Пусть в произвольный момент времени t расположение этих систем друг относительно друга имеет вид, изображенный на рис. 58. Скорость u направлена вдоль OO', радиус-вектор, проведенный из О в О', r0=ut.
Найдем связь между координатами произвольной точки А в обеих системах. Из рис. 58 видно, что
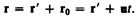 (34.1)
(34.1)
Уравнение (34.1) можно записать в проекциях на оси координат:
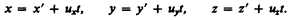 (34.2)
(34.2)
Уравнения (34.1) и (34.2) носят название преобразований координат Галилея.
В частном случае, когда система К' движется со скоростью т вдоль положительного направления оси х системы К (в начальный момент времени оси координат совпадают), преобразования координат Галилея имеют вид
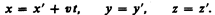
В классической механике предполагается, что ход времени не зависит от относительного движения систем отсчета, т. е. к преобразованиям (34.2) можно добавить еще одно уравнение:
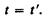 (34.3)
(34.3)
Записанные соотношения справедливы лишь в случае классической механики (u<<с), а при скоростях, сравнимых со скоростью света, преобразования Галилея заменяются более общими преобразованиями Лоренца* (§ 36).
* Х. Лоренц (1853—1928) — нидерландский физик-теоретик.
Продифференцировав выражение (34.1) по времени (с учетом (34.3)), получим уравнение
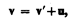 (34.4)
(34.4)
которое представляет собой правило сложения скоростей в классической механике.
Ускорение в системе отсчета К
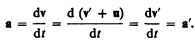
Таким образом, ускорение точки А в системах отсчета К и К', движущихся друг относительно друга равномерно и прямолинейно, одинаково:
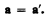 (34.5)
(34.5)
Следовательно, если на точку А другие тела не действуют (а=0), то, согласно (34.5), и а'=0, т. е. система К' является инерциальной (точка движется относительно нее равномерно и прямолинейно или покоится).
Таким образом, из соотношения (34.5) вытекает подтверждение механического принципа относительности: уравнения динамики при переходе от одной инерциальной системы отсчета к другой не изменяются, т. е. являютсяинвариантными по отношению к преобразованиям координат. Галилей обратил внимание, что никакими механическими опытами, проведенными в данной инерциальной системе отсчета, нельзя установить, покоится ли она или движется равномерно и прямолинейно. Например, сидя в каюте корабля, движущегося равномерно и прямолинейно, мы не можем определить, покоится корабль или движется, не выглянув в окно.

§ 35. Постулаты специальной (частной) теории относительности
Классическая механика Ньютона прекрасно описывает движение макротел, движущихся с малыми скоростями (v<<с). Однако в конце XIX в. выяснилось, что выводы классической механики противоречат некоторым опытным данным, в частности при изучении движения быстрых заряженных частиц оказалось, что их движение не подчиняется законам механики. Далее возникли затруднения при попытках применить механику Ньютона к объяснению распространения света. Если источник и приемник света движутся друг относительно друга равномерно и прямолинейно, то, согласно классической механике, измеренная скорость должна зависеть от относительной скорости их движения. Американский физик А. Майкельсон (1852—1913) в 1881 г., а затем в 1887 г. совместно с Е. Морли (американский физик, 1838—1923) пытался обнаружить движение Земли относительно эфира (эфирный ветер) —опыт Майкельсона — Морли, применяя интерферометр, названный впоследствии интерферометром Майкельсона (см. § 175). Обнаружить эфирный ветер Майкельсону не удалось, как, впрочем, не удалось его обнаружить и в других многочисленных опытах. Опыты «упрямо» показывали, что скорости света в двух движущихся друг относительно друга системах равны. Это противоречило правилу сложения скоростей классической механики.
Одновременно было показано противоречие между классической теорией и уравнениями (см. § 139) Дж. К. Максвелла (английский физик, 1831—1879), лежащими в основе понимания светакак электромагнитной волны.
Для объяснения этих и некоторых других опытных данных необходимо было создать новую механику, которая, объясняя эти факты, содержала бы ньютоновскую механику как предельный случай для малых скоростей (v<<с). Это и удалось сделать А. Эйнштейну, который пришел к выводу о том, что мирового эфира — особой среды, которая могла бы быть принята в качестве абсолютной системы, — не существует. Существование постоянной скорости распространения света в вакууме находилось в согласии с уравнениями Максвелла.
Таким образом, А. Эйнштейн заложил основыспециальной теории относительности.Эта теория представляет собой современную физическую теорию пространства и времени, в которой, как и в классической ньютоновской механике, предполагается, что время однородно (см. § 13), а пространство однородно (см. § 9) и изотропно (см. § 19). Специальная теория относительности часто называется такжерелятивистской теорией,а специфические явления, описываемые этой теорией, —релятивистскими эффектами.
В основе специальной теории относительности лежат постулаты Эйнштейна, сформулированные им в 1905 г.
I. Принцип относительности: никакие опыты (механические, электрические, оптические), проведенные внутри данной инерциальной системы отсчета, не дают возможности обнаружить, покоится ли эта система или движется равномерно и прямолинейно; все законы природы инвариантны по отношению к переходу от одной инерциальной системы отсчета к другой.
П. Принцип инвариантности скорости света: скорость света в вакууме не зависит от скорости движения источника света или наблюдателя и одинакова во всех инерциальных системах отсчета.
Первый постулат Эйнштейна, являясь обобщением механического принципа относительности Галилея на любые физические процессы, утверждает, таким образом, что физические законы инвариантны по отношению к выбору инерциальной системы отсчета, а уравнения, описывающие эти законы, одинаковы по форме во всех инерциальных системах отсчета. Согласно этому постулату, все инерциальные системы отсчета совершенно равноправны, т. е. явления (механические, электродинамические, оптические и др.) вовсех инерциальных системах отсчета протекают одинаково.
Согласно второму постулату Эйнштейна, постоянство скорости света — фундаментальное свойство природы, которое констатируется как опытный факт.
Специальная теория относительности потребовала отказа от привычных представлений о пространстве и времени, принятых в классической механике, поскольку они противоречили принципу постоянства скорости света. Потеряло смысл не только абсолютное пространство, но и абсолютное время.
Постулаты Эйнштейна и теория, построенная на их основе, установили новый взгляд на мир и новые пространственно-временные представления, такие, например, как относительность длин и промежутков времени, относительность одновременности событий. Эти и другие следствия из теории Эйнштейна находят надежное экспериментальное подтверждение, являясь тем самым обоснованием постулатов Эйнштейна — обоснованием специальной теории относительности.
§ 36. Преобразования Лоренца
Анализ явлений в инерциальных системах отсчета, проведенный А. Эйнштейном на основе сформулированных им постулатов, показал, что классические преобразования Галилея несовместимы с ними и, следовательно, должны быть заменены преобразованиями, удовлетворяющими постулатам теории относительности.
Для иллюстрации этого вывода рассмотрим две инерциальные системы отсчета: К (с координатами х, у, z) и К' (с координатами х', у', z'), движущуюся относительно К (вдоль оси х) со скоростью v = const (рис. 59). Пусть в начальный момент времени t=t'=0, когда начала координат О и О' совпадают, излучается световой импульс. Согласно второму постулату Эйнштейна, скорость света в обеих системах одна и та же и равна с. Поэтому если за время t в системе К сигнал дойдет до некоторой точки А (рис. 59), пройдя расстояние
х = ct, (36.1)
то в системе К' координата светового импульса в момент достижения точки А
х' = ct'. (36.2)
где t' — время прохождения светового импульса от начала координат до точки А в системе К'. Вычитая (36.1) из (36.2), получаем
х' – х = c(t' – t).
Так как х' ¹ х (система К' перемещается по отношению к системе К), то
t' ¹ t,
т. е. отсчет времени в системах К и К' различен — отсчет времени имеет относительный характер (в классической физике считается, что время во всех инерциальных системах отсчета течет одинаково, т. е. t=t').
Эйнштейн показал, что в теории относительности классические преобразования Галилея, описывающие переход от одной инерциальной системы отсчета к другой:
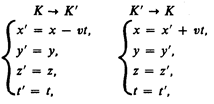
заменяются преобразованиями Лоренца, удовлетворяющими постулатам Эйнштейна (формулы представлены для случая, когда К' движется относительно К со скоростью v вдоль оси х).
Эти преобразования предложены Лоренцем в 1904 г., еще до появления теории относительности,как преобразования, относительно которых уравнения Максвелла (см. § 139) инвариантны.
Преобразования Лоренцаимеют вид
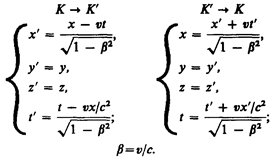 (36.3)
(36.3)
Из сравнения приведенных уравнений вытекает, что они симметричны и отличаются лишь знаком при v. Это очевидно, таккак если скорость движения системы К' относительно системы К равна v, то скорость движения К относительно К' равна –v.
Из преобразований Лоренца вытекает также, что при малых скоростях (по сравнению со скоростью с), т. е. когда b<<1, они переходят в классические преобразования Галилея (в этом заключается сутьпринципа соответствия), которые являются, следовательно, предельным случаем преобразований Лоренца. При v>c выражения (36.3) для х, t, х', t' теряют физический смысл (становятся мнимыми). Это находится, в свою очередь, в соответствии с тем, что движение со скоростью, большей скорости распространения света в вакууме, невозможно.
Из преобразований Лоренца следует очень важный вывод о том, что как расстояние, так и промежуток времени между двумя событиями меняются при переходе от одной инерциальной системы отсчета к другой, в то время как в рамках преобразований Галилея эти величины считались абсолютными, не изменяющимися при переходе от системы к системе. Кроме того, как пространственные, так и временные преобразования (см. (36.3)) не являются независимыми, поскольку в закон преобразования координат входит время, а в закон преобразования времени — пространственные координаты, т. е. устанавливается взаимосвязь пространства и времени. Таким образом, теория Эйнштейна оперирует не с трехмерным пространством, к которому присоединяется понятие времени, а рассматривает неразрывно связанные пространственные и временные координаты, образующие четырехмерное пространство-время.
§ 37. Следствия из преобразований Лоренца
1. Одновременность событий в разных системах отсчета. Пусть в системе К в точках с координатами x1 и x2 в моменты времени t1 и t2 происходят два события. В системе К' им соответствуют координаты 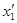 и
и 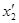 и моменты времени
и моменты времени 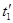 и
и 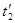 . Если события в системе К происходят в одной точке (x1 =х2)и являются одновременными (t1 =t2), то, согласно преобразованиям Лоренца (36.3),
. Если события в системе К происходят в одной точке (x1 =х2)и являются одновременными (t1 =t2), то, согласно преобразованиям Лоренца (36.3),

т. е. эти события являются одновременными и пространственно совпадающими для любой инерциальной системы отсчета.
Если события в системе К пространственно разобщены (х1 ¹ x2), но одновременны (t1 = t2), то в системе К', согласно преобразованиям Лоренца (36.3),
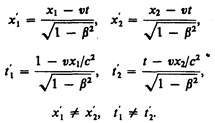
Таким образом, в системе К' эти события, оставаясь пространственно разобщенными, оказываются и неодновременными. Знак разности 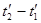 определяется знаком выражения v (x1 – x2), поэтому в различных точках системы отсчета К' (при разных v) разность
определяется знаком выражения v (x1 – x2), поэтому в различных точках системы отсчета К' (при разных v) разность 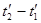 будет различной по величине и может отличаться по знаку. Следовательно, в одних системах отсчета первое событие может предшествовать второму, в то время как в других системах отсчета, наоборот, второе событие предшествует первому. Сказанное, однако, не относится к причинно-следственным событиям, так как можно показать, что порядок следования причинно-следственных событий одинаков во всех инерциальных системах отсчета.
будет различной по величине и может отличаться по знаку. Следовательно, в одних системах отсчета первое событие может предшествовать второму, в то время как в других системах отсчета, наоборот, второе событие предшествует первому. Сказанное, однако, не относится к причинно-следственным событиям, так как можно показать, что порядок следования причинно-следственных событий одинаков во всех инерциальных системах отсчета.
2. Длительность событий в разных системах отсчета. Пусть в некоторой точке (с координатой х), покоящейся относительно системы К, происходит событие, длительность которого (разность показаний часов в конце и начале события) t = t2 – t1, где индексы 1 и 2 соответствуют началу и концу события. Длительность этого же события в системе К'
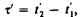 (37.1)
(37.1)
причем началу и концу события, согласно (36.3), соответствуют
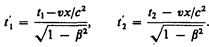 (37.2)
(37.2)
Подставляя (37.2) в (37.1), получаем
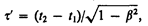
Дата добавления: 2017-04-20; просмотров: 407;
