Параллельное соединение

Системой с параллельным соединением элементов называется такая система, которая отказывает в том случае, если отказали все ее элементы.

Пример такой системы представлен на рис. 7.8.

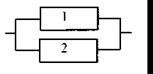
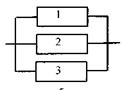
а) б)

Рисунок 4.8 - Системы с параллельным соединением

Случай, изображенный на рисунке 4.8, а, есть дублирование элементов.

На рисунке 4.8, б, система состоит из трех элементов.

Если отказывает любой из трех элементов - система остается работоспособной. Она будет работать и в том случае, если откажут любые два элемента, так как для обеспечения нормального функционирования системы достаточно функционирование всего одного элемента.

Определим надежность функционирования системы на рисунке 4.8, а:

P₁(t) - вероятность безотказной работы первого элемента;

Р₂ (t) - вероятность безотказной работы второго элемента.

Тогда

F₁(t) = 1 – P₁(t) - вероятность отказа первого элемента;

F₂(t) = 1 - Р₂ (t) - вероятность отказа второго элемента.

Вероятность отказа всей системы:

F_с(t) = [1 – P₁(t)] · [1 – P₂(t)]. (4.6)

Вероятность безотказной работы всей системы:

Р_с(t) = 1 - F_с(t) = 1 - [1 – P₁(t)] · [1 – P₂(t)]. (4.7)

В частном случае, если параллельно включенные элементы имеют одинаковую надежность, т.е.:

P₁(t) = P₂(t) = P(t). (4.8)

Будем иметь:

Р_с(t) = 1 - [1 – P₁(t)]². (4.9)

На рисунке 4.9 показана система кругов Р₁, Р₂, Р₃, все точки которых соответствуют работоспособности элементов системы, т.е. любая точка заштрихованного множества объединения отвечает состоянию работоспособности системы

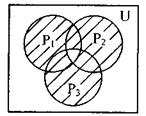
Рисунок 4.9 - Параллельное соединение

Таким образом, расчетная формула для определения показателя надежности системы с параллельным соединением:

Р_с(t) = 1 - [1 – P₁(t)] · [1 – P₂(t)] · ...· [1 – P_n(t)]. (4.10)

Выводы из формулы следующие: