Параметры статистического распределения.
Для проверки гипотез о виде эмпирического закона распределения наибольшее распространение получили критерии Пирсона и Колмогорова.
Критерий Колмагорова
Строим статистическую интегральную функцию распределения F*(t) и теоретическую интегральную функцию распределения F(t) предполагаемого закона.
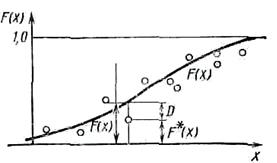
Рисунок 3.2 – Теоретическая и экспериментальная функция распределения
Оцениваем максимальную величину расхождения между функциями:
Dmax=max |F*(t) - F(t)|,
где F*(t) – статистическая функция; F(t) – теоретическая функция;
Определяется условная интенсивность:
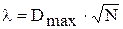 .
.
В зависимости от l находится табличное значение вероятности Р(l).
Если Р(l) ³ 0,5, то гипотеза не противоречит опытным данным.
Критерий Пирсона
Требуется определить согласие гипотезы о законе распределения с результатами эксперимента и параметры распределения.
Если 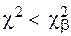 , то гипотеза подтверждается.
, то гипотеза подтверждается.
Доказано, что при n®¥ случайная величина х имеет c2 – распределение:
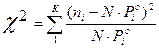
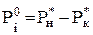 ;
; 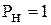 .
.
где 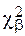 - табличное значение (выбирается по Р и r); r = K – S + 1 – число степеней свободы; K – число интервалов; S – число обязательных связей: S =2 для нормального закона; S =1 для экспоненциального закона; S = 3 для закона Вейбула.
- табличное значение (выбирается по Р и r); r = K – S + 1 – число степеней свободы; K – число интервалов; S – число обязательных связей: S =2 для нормального закона; S =1 для экспоненциального закона; S = 3 для закона Вейбула.
Лекция 4. Надежность сложных систем. Сложная система и ее характеристики. Структурный анализ систем технологического оборудования
Дата добавления: 2017-02-20; просмотров: 313;
