Основные показатели динамического ряда. Уровень динамического ряда
Всесторонний анализ динамического ряда позволяет вскрывать и характеризовать закономерности, проявляющиеся на разных этапах развития явлений, выявить тенденции и особенности их развития. В процессе анализа динамического ряда используют следующие показатели динамики: уровни ряда, абсолютные приросты уровней, темпы роста, темпы прироста, абсолютные значения одного процента прироста.
Исходные значения признака, образующие динамический ряд, называются уровнямиряда. Они служат начальной базой для расчета и оценки различных показателей динамики. В большинстве случаев этот расчет основан на сравнении между собой уровней ряда.
Тот уровень, который является базой для сравнения и с которым производится сравнение других уровней, называется базисным. За базу сравнения применяют либо начальный (первый), либо предыдущий, или любой уровень динамического ряда. Базисный уровень в статистике обычно принято обозначать У0. Уровень ряда, который сравнивается с базисным, называется текущим (отчетным). Текущие уровни могут иметь следующие обозначения: У1, У2, У3…Уn.
Если все уровни динамического ряда сравниваются с одним и тем же уровнем, то полученные показатели динамики называются базисными. Если же каждый последующий уровень ряда сравнивается с каждым предыдущим, то полученные динамические показатели называются цепными.Эти показатели представляют собой как бы отдельные звенья единой «цепи», связывающей уровни ряда.
В динамическом ряду приводится несколько последовательных уровней, среди которых особый интерес представляют начальный, срединный и конечный уровни ряда. Первый член динамического ряда называется начальным уровнем. Срединный уровень ряда находится обычно по способу определения медианы: при нечетном числе уровней срединным считается тот, который находится в середине ряда; при четном – срединный уровень рассчитывают как полусумму из двух смежных уровней, находящихся в средине динамического ряда. Последний член динамического ряда принято называть конечным.
Допустим, имеются данные об объеме товарных овощей в административном районе, тыс. тонн: 2006 г. – 20; 2007 г. – 18; 2008 г. – 15; 2009 г. – 19; 2010 г. – 22. В этом динамическом ряду начальным уровнем является объем товарных овощей в 2006 г., срединным – в 2008 г., и конечным – объем товарных овощей в 2010 г.
Для общей характеристики явления за весь период целесообразно рассчитать средний уровень из всех членов динамического ряда. При этом способ расчета среднего уровня зависит от вида динамического ряда.
При расчете среднего уровня в моментном динамическом ряду (с равными промежутками между моментами) рекомендуется использовать способ средней хронологической простой величины.
Следует обратить внимание на то, что уровней в моментном ряду всегда на единицу больше числа интервальных промежутков между моментами. Например, в каждом квартале, включающем три месяца, число моментов и соответствующих им уровней ряда равно четырем. Соответственно этому моментный ряд за полный год всегда насчитывает пять квартальных или 13 помесячных моментов и столько же уровней.
Допустим, необходимо рассчитать среднее поголовье коров за первый квартал года в сельскохозяйственной организации по следующим данным:
Дата 1.01 1.02 1.03 1.04
Число голов 800 810 830 840
Приведенные данные показывают, что поголовье коров зафиксировано по состоянию на первое число каждого месяца. При этом предполагается, что с 1.02 по 1.04 поголовье на конец каждого месяца в первом квартале существенно не отличается от поголовья по смежным начальным датам: поголовье на 1.02 ≈ поголовью на 31.01; на 1.03 ≈ на 28 (29). 02 и т.д. Кроме того, что помесячные промежутки между указанными моментами приблизительно равны между собой и составляют один месяц. Предполагается, что изменение численности коров в промежутках между указанными датами шло более-менее равномерно. Следовательно, для расчета среднего квартального поголовья можно воспользоваться формулой хронологической моментного ряда. Подставим в формулу исходные данные и получим:
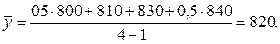
Таким образом, в сельскохозяйственной организации в среднем за первый квартал имелось 820 коров.
В тех случаях, когда моментный ряд динамики представлен неравными промежутками между датами, средний уровень ряда обычно рассчитывают по способу средней арифметической взвешенной, т.е.
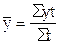 , (9.1)
, (9.1)
где у – постоянные уровни ряда: t – промежутки времени с постоянными уровнями.
Пример. Имеются данные о численности работников в фермерском хозяйстве:
Дата 1.08 10.08 17.08 31.08
Численность 12 15 20 12
Необходимо рассчитать среднемесячную численность работников за август. Из приведенных данных видно, что между указанными датами были различные промежутки времени (в днях) и существенно различалась численность работников. Поэтому при определении средней численности работников за весь август необходимо их число за каждый отдельный промежуток взвесить через количество календарных дней, т.е. применить формулу (10.1):
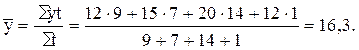
Таким образом, в фермерском хозяйстве в течение августа работало ежедневно в среднем 16,3 работника.
При расчете среднего уровня в периодическом ряду динамики обычно рекомендуют использовать способ средней арифметической простой величины, т.е.
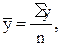 (9.2)
(9.2)
где у – уровни периодического ряда; n – число уровней в ряду.
Предположим, имеются данные о реализации льнотресты в сельскохозяйственной организации по месяцам четвертого квартала:
Месяцы Октябрь Ноябрь Декабрь
Объем, т 500 400 300
Необходимо найти среднемесячный объем реализации льнотресты. Для этого воспользуемся формулой (10.2) и получим:
 .
.
Следовательно, среднемесячная реализация льнотресты в четвертом квартале составила 400 т.
Дата добавления: 2017-04-20; просмотров: 806;
