Абсолютные приросты уровней
Одним из наиболее простых показателей развития динамики является абсолютный прирост уровня.
Абсолютным приростом называется разность двух уровней динамического ряда.Измеряется в тех же единицах, в которых показаны уровни ряда динамики. Если абсолютный прирост уровня обозначим через ΔУ, уровень последующего периода – Уi, предыдущего – Уi-1, то значение абсолютного прироста алгебраически можно выразить так:
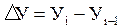 , (9.3)
, (9.3)
где 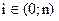 .
.
Абсолютный прирост выражает абсолютное изменение уровней и показывает, на сколько единиц увеличился или уменьшился последующий уровень динамического ряда по сравнению с предыдущим.
Характер динамического ряда может принимать разнообразные формы. Если уровни ряда от начального к конечному увеличиваются, то такой динамический ряд будет иметь положительные абсолютные приросты.
Например, необходимо найти абсолютный прирост государственных закупок сахарной свеклы административного района в 2010 г. по сравнению с 2009 г. по следующим данным (тыс. т), если было закуплено соответственно 145 и 140 тыс. тонн. Абсолютный прирост составил (по формуле (9.3): 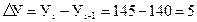 тыс. тонн, т.е. объем госзакупок в 2010 г. возрос по сравнению с 2009 г. на 5 тыс. тонн.
тыс. тонн, т.е. объем госзакупок в 2010 г. возрос по сравнению с 2009 г. на 5 тыс. тонн.
В тех случаях, когда каждый последующий уровень ряда ниже предыдущего (базисного), имеет место не абсолютный прирост, а абсолютное снижениеуровня.
Определим абсолютное снижение объема переработки картофеля в перерабатывающей организации в 2010 г. по сравнению с 2008 г., если за этот период переработка снизилась со 100, 1 до 95,3 тыс. т.
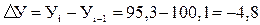 тыс. тонн.
тыс. тонн.
Это означает, что объем переработки картофеля уменьшился на 4,8 тыс. тонн.
Абсолютные приросты могут быть рассчитаны базисным и цепным способами. Абсолютные приросты, полученные в результате сравнения текущих (отчетных) уровней с постоянными (базисными), называют базисными.Приросты, которые получены при сравнении каждого последующего уровня с предыдущим, называются цепными.
Исчислим базисные и цепные абсолютные приросты урожайности картофеля в сельскохозяйственной организации по следующим данным (табл. 9.2).
Т а б л и ц а 9.2. Урожайность картофеля в сельскохозяйственной
организации «Днепр»
| Годы | Урожайность, ц/га | Абсолютный прирост, ц/га | |
| По сравнению с 2008 годом (базисный) | По сравнению с предыдущим годом (цепной) | ||
| У0=273 | – | – | |
| У1=277 | У1 –У0=4 | У1–У0=4 | |
| У2=304 | У2–У0=31 | У2–У1=27 |
Базисные и цепные абсолютные приросты имеют общую для их базу и поэтому связаны между собой следующими зависимостями:
• во-первых, сумма n последовательных цепных абсолютных приростов, начиная с первого, равна n-ому базисному абсолютному приросту, т.е.
Σ ΔУц=ΔУб. (9.4)
• во-вторых, разность между смежными (последующим и предыдущим) базисными абсолютными приростами равна соответствующему цепному абсолютному приросту, т.е.
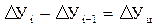 . (9.5)
. (9.5)
Приведенная зависимость может быть при необходимости использована для преобразования цепных абсолютных приростов в базисные и наоборот. Например, имеются данные о цепных приростах подекадного объема переработки зерна на мелькомбинате: за 1 декаду –– 10 т, за 2 –– 8 т, за 3 декаду –– 6 т. Необходимо рассчитать базисные абсолютные приросты объема переработки зерна за каждую декаду.
Для нахождения базисных абсолютных приростов воспользуемся первой зависимостью по формуле (10.4). В результате получим: базисный абсолютный прирост за первую декаду ΔУ1=0+10=10 т; за вторую –– ΔУ2=10+8=18 т; за третью –– ΔУ3=10+8+6=24 т.
Если есть необходимость найти цепные абсолютные приросты по приведенным базисным приростам, то можно воспользоваться второй зависимостью по формуле (10.5). Допустим, имеются данные о базисных абсолютных приростах помесячного объема переработки сахарной свеклы на сахарном комбинате: в ноябре –– 240 тыс. т, в декабре –– 210, в январе –– 220, в феврале –– 150 тыс. т. По этим данным необходимо рассчитать цепные абсолютные приросты помесячного объема переработки сахарной свеклы. Согласно второй зависимости имеем:
за ноябрь ΔУ1=240-0=240 тыс. т. за январь ΔУ3=220-210=10 тыс. т.
за декабрь ΔУ2=210-240=-30 тыс. т. за февраль ΔУ4=150-220=-70 тыс. т.
В статистико-экономических исследованиях часто приходится рассчитывать средний абсолютный прирост уровней динамического ряда.
Средний абсолютный прироствсегда является периодическим показателем. Поэтому он исчисляется по формуле простой средней арифметической из цепных абсолютных приростов за последовательные и более-менее равные по продолжительности периоды:
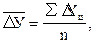 (9.6)
(9.6)
где: 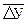 – средний абсолютный прирост; n – число цепных абсолютных приростов.
– средний абсолютный прирост; n – число цепных абсолютных приростов.
Пример. Определить среднемесячный абсолютный прирост объема переработки молока в перерабатывающей организации за первый квартал (табл. 10.3).
Т а б л и ц а 9. 3. Объем переработки молока
| Месяцы | Переработано, т | Помесячный абсолютный прирост (цепной), т |
| Январь | У0=1470 | ΔУ0=0 |
| Февраль | У1=1867 | ΔУ1=397 |
| Март | У2=1960 | ΔУ2=93 |
| Итого | - | ΣΔУ=490 |
Используя формулу (10.6), находим среднемесячный абсолютный прирост переработки молока:
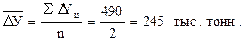
Согласно первой зависимости общая сумма цепных абсолютных приростов (Σ ΔУц) ряда динамики представляет собой базисный абсолютный прирост за весь изучаемый период в целом (Уn – У0). Число приростов (n) равно числу уровней ряда минус единица 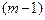 . Следовательно, средний абсолютный прирост можно выразить в виде:
. Следовательно, средний абсолютный прирост можно выразить в виде:
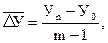 (10.7)
(10.7)
где Уп – значение конечного уровня динамического ряда; У0 – начальный уровень ряда; 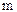 – число уровней ряда.
– число уровней ряда.
Пример.Найти среднегодовой абсолютный прирост валового сбора фруктов и ягод в специализированной сельскохозяйственной организации за период 2008 – 2010 гг., если известно, что в 2008 г. было собрано 1596 т, а в 2010 г. – 1823 т. Расчет среднегодового абсолютного прироста ведем по формуле (10.6), т.е. 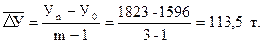
Следовательно, за изучаемый период среднегодовой абсолютный прирост валового сбора фруктов и ягод составил 113,5 т.
Дата добавления: 2017-04-20; просмотров: 720;
