Темпы роста уровней
Для характеристики относительной скорости изменения уровня динамического ряда используется показатель темпа роста. Это выраженное в процентах отношение одного уровня динамического ряда к другому, принятому за базу сравнения. Темпы роста могут быть выражены в форме коэффициентов или процентов.
Коэффициент роста показывает, во сколько раз сравниваемый (текущий) уровень больше базисного:
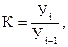 (9.8)
(9.8)
где К – коэффициент роста уровней; Уi – уровень последующего периода;
Уi-1 – уровень предыдущего периода.
Коэффициент роста, выраженный в процентах, называется темпом:
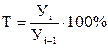 (9.9)
(9.9)
Пример. Валовая продукция маслосырзавода в 2010 г. составила 32,0 млрд. рублей, в 2009 г. – 30,7 млрд. рублей. Необходимо найти темп роста валовой продукции в 2010 г. по сравнению с 2009 г.
Для решения воспользуются формулами (10.8 и 10.9). Во-первых,
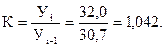
Следовательно, производство валовой продукции маслосырзавода в 2010 г. увеличилось по сравнению с 2009 г. в 1,042 раза.
Во-вторых, 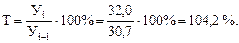
Это означает, что объем валовой продукции в 2010 г. составил 104,2 % объема продукции 2009 года.
Темпы роста могут быть рассчитаны базисным и цепным способами.
Допустим, необходимо исчислить базисные и цепные темпы роста урожайности картофеля в сельскохозяйственной организации «Днепр» (табл. 9.4).
Т а б л и ц а 9.4. Динамика урожайности картофеля в сельскохозяйственной
Организации
| Годы | Урожайность, ц/га | Темп роста, % | |
| По сравнению с 2007 г. (базисные) | По сравнению с предыдущим годом. (цепные) | ||
| - | |||
| 105,4 | 105,4 | ||
| 106,9 | 101,5 | ||
| 117,4 | 109,7 |
Между базисными и цепными темпами роста, выраженными в форме коэффициентов, имеется определенная взаимосвязь, которая заключается в следующем:
• во-первых, произведение последовательных цепных темпов роста равно базисному темпу роста за соответствующий период;
• во-вторых, частное от деления последующего базисного темпа роста на предыдущий равно соответствующему цепному темпу роста.
Указанные зависимости между темпами роста можно использовать для преобразования базисных темпов в цепные и наоборот, особенно в тех случаях, когда неизвестны абсолютные уровни динамики.
Пример. Известно, что производительность труда в фермерском хозяйстве в 2010 г. возросла по сравнению с 2006 г. в 1,2 раза, а в 2006г. по сравнению с 2002 г. – в 1,3 раза. Необходимо определить, как повысилась производительность труда в 2010 г. по сравнению с 2002 г., т.е. найти темп роста производительности труда за период 2002 – 2010 гг. С этой целью рассуждаем так: поскольку коэффициенты роста за первый и второй периоды –– цепные, то базисный коэффициент за весь промежуток времени равен их произведению, т.е. Кб=1,2 · 1,3=1,56. Это означает, что базисный темп роста составил 156 %, т.е. в 2010 г. производительность труда в фермерском хозяйстве повысилась по сравнению с 2002 г. в 1,56 раза (156 %).
Темпы роста уровней динамического ряда по отдельным периодам, как правило, неодинаковы и обнаруживают некоторые колебания. Вследствие этого обычно возникает необходимость исчисления среднего темпа роста уровней за весь изучаемый период.
В отличие от абсолютного прироста за весь период, который представляет собой сумму абсолютных приростов за каждый отдельный промежуток времени, общий показатель темпа роста –– это произведение цепных коэффициентов (темпов) роста за каждый промежуток времени, т.е. коэффициенты связаны между собой знаком произведения. Поэтому для определения среднего темпа роста необходимо применить среднюю геометрическую простую, т.е.
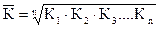 (9.10)
(9.10)
где 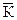 –– средний коэффициент роста за весь период; К1, К2, К3….Кn –– цепные коэффициенты роста за каждый отдельный промежуток времени; n –– число темпов роста.
–– средний коэффициент роста за весь период; К1, К2, К3….Кn –– цепные коэффициенты роста за каждый отдельный промежуток времени; n –– число темпов роста.
Например, валовая продукция в сельскохозяйственной организации «Днепр» за период 2008 – 2010 г. имела следующие коэффициенты роста: 2008 г. – 1,09; 2009 – 1,02; 2010 – 1,04 раза. По этим данным необходимо найти среднегодовой темп роста валовой продукции. Применим для решения формулу (9.10) и получим 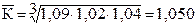 раза (105,0 %).
раза (105,0 %).
Если произведение цепных темпов заменить соответствующим базисным темпом роста за весь изучаемый период, то получим формулу среднего темпа роста:
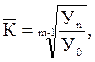 (9.11)
(9.11)
где 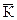 –– средний темп роста; Уп –– конечный уровень ряда; У0 –– начальный уровень; m –– число уровней в динамическом ряду.
–– средний темп роста; Уп –– конечный уровень ряда; У0 –– начальный уровень; m –– число уровней в динамическом ряду.
Применение формулы (9.11) по сравнению с предыдущей (9.10) позволяет значительно упростить расчет среднего темпа роста. Кроме того, формулой (9.11) можно пользоваться в тех случаях, когда имеются значения только начального и конечного уровней. Допустим, необходимо определить среднегодовой темп роста площади пахотных земель в фермерском хозяйстве за период 2001 – 2010 гг., если в начале этого периода фермер имел 10 га, а в конце –– 100 га земель.
Расчет искомого среднегодового темпа роста ведем по формуле (9.11), т.е.
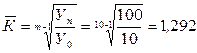 (129,2 %).
(129,2 %).
Следовательно, ежегодный темп роста площади пахотных земель в фермерском хозяйстве в среднем составлял 129,2 %.
Дата добавления: 2017-04-20; просмотров: 588;
