Логико-экономические стандартные приемы экономического анализа
К числу широко распространенных способов статистики, используемых в финансово-экономическом анализе, относятся следующие: сводка и группировка, абсолютные и относительные величины, средние величины, ряды динамики, сравнение, индексы, графический и т.д.
Изучение любого показателя начинается, как правило, с анализа его абсолютной величины, которая сравнивается с абсолютной величиной этого показателя в предшествующем периоде, с нормативной, плановой величиной. Сравнение проводится также со средней величиной, исчисленной по совокупности аналогичных показателей, с лучшим показателем. Сравнение является на первый взгляд одним из самых простых способов анализа, однако необходимо учесть, что адекватные выводы могут быть получены только при сравнении сопоставимых показателей. Например, сравнивая показатели выручки от продаж за отчетный год и предшествующий, необходимо учесть влияние инфляционных процессов, структурных, организационных и прочих изменений, произошедших в отчетном периоде. Чтобы добиться сопоставимости данных, необходимо скорректировать сумму выручки отчетного года с учетом влияния имевших место факторов.
Относительные величины используются в анализе динамики различных показателей, а также в процессе изучения структурных показателей и их изменения. Выводы об изменениях показателей в динамике (во времени) можно сделать, рассчитав темпы роста (снижения) в виде отношения величины соответствующего показателя к его базисной величине (базисный темп роста) или к его величине за предшествующий период (цепной темп роста).
Важное значение в экономическом анализе имеют средние величины, которые позволяют обобщить совокупность типичных, однородных показателей хозяйственной деятельности, выявить закономерности и тенденции: средняя арифметическая, средняя взвешенная, средняя геометрическая, средняя хронологическая моментного ряда динамики и т.д.
Способ группировки позволяет изучить различные экономические показатели с точки зрения выявления между ними причинно-следственных связей. В процессе использования способа группировки производится определенная классификация показателей, а также факторов (причин), влияющих на изменение этих показателей. Группировку целесообразно применять в тех случаях, когда имеется основание для предположения, что между изменением данного экономического показателя и фактора (или нескольких факторов) имеется связь. Для доказательства этого предположения составляется таблица по какому-либо группировочному признаку (признакам) с заданными интервалами возрастания (убывания) его значения, и производится отбор показателей из совокупности исходных данных. Способ группировки может применяться, например, при изучении зависимости между размером производственной площади предприятий, входящих в состав производственного объединения (отрасли), и изменением различных показателей хозяйственной деятельности, в частности, уровня рентабельности продаж, рентабельности капитала, производительности труда работников и т.п.
Методы факторного анализа.
Одной из главных задач анализа является изучение причин, влияющих на изменение различных экономических показателей оценки деятельности организации. Целью факторного анализа является количественное измерение влияния каждого отдельно взятого фактора.
Экономические показатели рассматриваются в анализе как результат воздействия других показателей – факторов. Факторы – это причины, воздействующие на изучаемый экономический показатель, которые в результате анализа получают количественную и качественную оценку своего воздействия на результативный показатель. Разделение экономических показателей хозяйственной деятельности организации на результативные и факторные достаточно условно, так как практически каждый результативный показатель может быть использован в качестве факторного, оказывающего влияние на другой показатель более высокого порядка и наоборот.
Общепринятая классификация факторов предполагает разделение их на внешние (не зависящие от деятельности организации) и внутренние (зависящие от деятельности организации). К внешним факторам относятся внешнеэкономические условия хозяйствования (система рыночных, финансовых отношений, налоговая среда, уровень платежеспособного спроса и т.п.), социальные условия, природные условия. Внутренние факторы можно подразделить на производственные (производственные ресурсы, организационно-технический уровень производства) и непроизводственные (снабжение, сбыт, природоохранные мероприятия, социальные аспекты и т.п.).
В экономическом анализе исследуются факторные модели, отражающие функциональные зависимости (детерминированные, жесткие связи), а также стохастические (вероятностные).
Важным моментом факторного анализа является выбор модели, адекватно отражающей зависимость между результативным показателем и влияющими на него факторами (причинами). В детерминированных (жестких, функциональных) факторных моделях выделяется три основных типа:
· мультипликативная:
y = 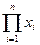 = x1 ∙ x 2 ,…∙ x n;
= x1 ∙ x 2 ,…∙ x n;
· аддитивная:
y = 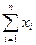 = x 1 + x 2 + … + x n ;
= x 1 + x 2 + … + x n ;
· кратная:
y = 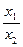 ; y =
; y = 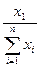 ; у =
; у = 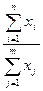 ; у =
; у = 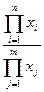 ,
,
где y – результативный показатель;
xi - факторы (факторные показатели).
Факторный анализ основан на принципе элиминирования, то есть устранения (игнорирования) влияния всех других факторов (причин) на изменение результативного (итогового) показателя, кроме одного.
Для выявления и измерения их воздействия используются определенные методики факторного анализа, в процессе реализации которых применяются различные методы факторного анализа:
q балансовый;
q индексный;
q цепных подстановок;
q абсолютных разниц;
q относительных разниц;
q интегральный;
q дифференцирования.
Балансовый метод используется, например, для расчета влияния остатков готовой продукции на начало и конец отчетного периода, объема произведенной продукции на изменение объема реализованной готовой продукции. Воспользовавшись базисными (или плановыми) и отчетными величинами этих показателей, расчет можно провести с использованием следующей формулы:
Ргп = ОгпH + Пгп - ОгпK,
где Ргп – объем реализованной готовой продукции за период, тыс.руб.;
Огпн - остатки готовой продукции на начало периода, тыс.руб.;
Пгп – объем произведенной готовой продукции за период, тыс.руб.;
Огпк - остатки готовой продукции на конец периода, тыс.руб.
Для расчета влияния факторов на изменение объема реализованной готовой продукции за период необходимо определить отклонения отчетных факторов от базисных (или плановых) значений. Положительные значения полученных отклонений будут соответствовать положительному значению влияния каждого из факторов. Исключение будет составлять отклонение по остаткам готовой продукции на конец периода. Для определения влияния этого фактора на объем продаж продукции величину полученного отклонения нужно взять с противоположным знаком, так как из формулы видна обратная связь между ними. Алгебраическая сумма влияния всех трех факторов должна соответствовать отклонению по результативному показателю. Расчет с использованием балансового метода приведен в табл. 1.4.
Таблица 1.4
Расчет влияния факторов на объем продаж
готовой продукции балансовым методом
тыс.руб.
| Показатели | Базисный период | Отчетный период | Отклонение (гр.3-гр.2) | Влияние факторов |
| Остатки готовой продукции на начало периода | ||||
| Объем произведенной готовой продукции | ||||
| Остатки готовой продукции на конец периода | -3 | |||
| Объем реализованной готовой продукции |
Как видно из таблицы 1.4, прирост объема продаж продукции в отчетном периоде по сравнению с базисным составил 44 тыс.руб. Это связано с влиянием трех факторов: изменением остатков готовой продукции на начало и конец периода и изменением объема произведенной продукции, причем влияние перечисленных факторов было неоднозначным. Положительное влияние на рост продаж готовой продукции в отчетном периоде оказало увеличение ее производства (+45 тыс.руб.), а также изменение ее остатков на начало периода (+2 тыс.руб.) Вместе с тем имело место негативное влияние увеличения остатков готовой продукции на конец периода, которое уменьшило объем продаж продукции в отчетном периоде на 3 тыс.руб. Совокупное влияние всех трех факторов на изменение объема продаж готовой продукции составило: +2+45-3 = 44 тыс.руб., что соответствует отклонению отчетного результативного показателя от базисного (44 тыс.руб.).
Индексный метод также широко применяется в решении задач факторного анализа. Он дает возможность разложить по факторам, как относительное отклонение, так и абсолютное отклонение результативного показателя. В качестве примера можно привести определение влияния на выручку от продаж двух факторов: физического объема реализованной продукции (в количественном выражении) и цен на продукцию. Для этого необходимо воспользоваться системой взаимосвязанных индексов:
IN = 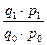 ; IN =
; IN = 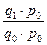 ∙
∙ 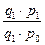 ; IN = Iq ∙ I p ,
; IN = Iq ∙ I p ,
где IN - общий (результативный) индекс выручки от продаж;
Iq - факторный индекс физического объема реализованной продукции;
I p - факторный индекс цен;
q0 , q1 - физический объем реализованной продукции в базисном и отчетном периодах;
p0 , p1 – цены базисного и отчетного периодов.
Приведенные формулы показывают, что общее относительное изменение выручки от продажи продукции образуется как произведение относительных изменений двух факторов: физического объема реализованной продукции и цен. Абсолютное отклонение (прирост) результативного показателя – выручки от продажи продукции (ΔN) определяется следующим образом:
ΔN = N1 – N0 = q1p1 - q0p0 ,
где N1 – сумма выручки от продаж за отчетный период;
N0 – сумма выручки от продаж за предыдущий период.
Это отклонение образуется под влиянием изменений физического объема реализованной продукции и цен. Для определения влияния каждого фактора необходимо воспользоваться приемом элиминирования, то есть при расчете влияния одного фактора устранить влияние другого. Разница между числителем и знаменателем расчета индекса физического объема ( 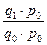 ) покажет влияние изменения количества реализованной продукции на сумму выручки от продаж (ΔNq), так как в этом случае будет элиминировано (устранено) влияние цен. Разница между числителем и знаменателем расчета индекса цен (
) покажет влияние изменения количества реализованной продукции на сумму выручки от продаж (ΔNq), так как в этом случае будет элиминировано (устранено) влияние цен. Разница между числителем и знаменателем расчета индекса цен ( 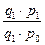 ) покажет влияние изменения цен сумму выручки от продаж (ΔNp), так как в этом случае будет элиминировано (устранено) влияние количества реализованной продукции. Формулы для расчета влияния факторов следующие:
) покажет влияние изменения цен сумму выручки от продаж (ΔNp), так как в этом случае будет элиминировано (устранено) влияние количества реализованной продукции. Формулы для расчета влияния факторов следующие:
ΔNq = q1p0 - q0p0; ΔNp = q1p1 - q1p0; ΔNq + ΔNp= ΔN
С помощью приведенных выше формул произведем расчет влияния факторов на изменение результативного показателя индексным методом, используя следующие данные: выручка от продажи продукции в отчетном году составила 1200 тыс.руб., в предшествующем (базисном) – 1000 тыс.руб., рост цен в отчетном периоде составил 5%. Необходимо определить влияние изменение физического объема реализованной продукции и изменения цен на рост выручки от продажи продукции в отчетном году по сравнению с предшествующим годом.
Так как рост цен составил 5%, то можно считать, что индекс цен равен 1,05 (или 105%):
I p = 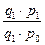 , откуда q1p0 = 1200 : 1,05 = 1143 тыс.руб.
, откуда q1p0 = 1200 : 1,05 = 1143 тыс.руб.
Теперь можно определить влияние каждого из факторов на рост выручки от продажи продукции:
· влияние изменения физического объема реализованной продукции:
ΔNq = q1p0 - q0p0 = 1143 – 1000 = 143 тыс.руб.;
· влияние изменения цен:
ΔNp = q1p1 - q1p0 = 1200 – 1143 = 57 тыс.руб.
Как видно из расчетов, на рост выручки от продажи продукции в бόльшей степени повлияло увеличение физического объема реализованной продукции. Суммарное влияние факторов составило 200 тыс.руб., что соответствует абсолютному приросту выручки от продажи продукции (1200 – 1000 = 200 тыс.руб.).
Использование индексного метода в решении задач факторного анализа имеет некоторые ограничения: количество факторов, включенных в аналитическую формулу, – не более двух, а результативный показатель представляется только в виде произведения факторов. При исследовании других видов факторных зависимостей с бóльшим числом факторов используются другие методы факторного анализа: цепных подстановок, интегральный, логарифмический и др.
Метод цепных подстановок используется для расчета влияния факторов на результативный показатель с использованием различных факторных моделей, выраженных в виде функции двух и более переменных (алгебраической суммы, произведения или частного от деления одних переменных на другие).
Последовательность действий такова. Вначале выбирается тот или иной вид формулы (модели факторного анализа), в которую включается необходимое количество факторов (аргументов), влияющих на результативный показатель (функцию). Далее формируется исходная информация о показателях и факторах, включенных в модель. Для этого могут быть использованы данные отчетности за два временных отрезка, например, отчетного и предшествующего (вместо показателей предшествующего периода могут быть использованы плановые или нормативные данные). Следующим этапом являются расчеты значений результативного показателя по выбранной формуле. Количество таких расчетов всегда на одно больше, чем количество факторов, включенных в формулу (модель). Значения факторов в расчетах последовательно заменяются с предшествующих (или плановых) на отчетные. В первом расчете все значения факторов – предшествующего периода (плановые), следовательно, и значение результативного показателя так же будет за предшествующий период. Во втором и в каждом последующем расчете предшествующее значение одного из факторов заменяется на его отчетное значение (все остальные факторы остаются без изменения). В результате такого расчета величина результативного показателя принимает скорректированный вид, причем в каждом последующем расчете количество отчетных значений факторов становится на одно больше, чем в предыдущем расчете. Для установления последовательности замены значений факторов с предшествующих на отчетные исходят из того, что в первую очередь замены производятся по экстенсивным (количественным) факторам, далее – по интенсивным (качественным). Замены предшествующих значений факторов на отчетные производятся до получения отчетного значения результативного показателя. Далее из каждого последующего результативного показателя вычитается предыдущее его значение, тем самым определяется влияние на результативный показатель того фактора, значение которого в последующем расчете было заменено с предшествующего на отчетное. Таким образом определяется влияние каждого фактора, включенного в модель. Алгебраическая сумма влияния всех факторов должна соответствовать абсолютному отклонению отчетного значения результативного показателя от его значения за предшествующий период. Далее делается вывод о характере и степени воздействия каждого фактора на результативный показатель. Покажем использование способа цепных подстановок на конкретном примере, используя данные табл. 1.5.
Таблица 1.5
Расчет влияния факторов на изменение выручки от продажи продукции
| Показатели | Усл. обозн. | Пред. год | Отчет. год | 1-й расчет | 2-й расчет | 3-й расчет |
| Материальные расходы, тыс. руб. | М | |||||
| Коэффициент материалоотдачи | λМ | |||||
| Выручка от продажи продукции, тыс.руб. | N |
В приведенном примере результативным показателем является выручка от продажи продукции (N), а факторами, оказывающими на нее влияние, - материальные расходы (М) и среднегодовой выпуск продукции в расчете на одного работника (λМ). Факторная зависимость выражается следующей формулой: N = М * λМ , используя которую делаются подстановки значений факторов:
1. 300 ∙ 60 = 18000 тыс.руб. (Nпред);
2. 326 ∙ 60 = 19560 тыс.руб. (Nскорректир);
3. 326 ∙ 72 = 23472 тыс.руб. (Nотч).
Расчет влияния каждого фактора на изменение выручки от продажи продукции:
· влияние изменения материальных расходов:
ΔNМ = 19560 – 18000 = 1560 тыс.руб.
· влияние изменения материалоотдачи:
ΔNλМ: = 23472 – 19560 = 3912 тыс.руб.
Алгебраическая сумма влияния двух факторов (1560+3912=5472 тыс.руб.), соответствует приросту результативного показателя – выручки от продажи продукции в отчетном году по сравнению с предшествующим годом (23472 – 18000 = 5472 тыс.руб.).
Для определения степени (доли) участия каждого из двух факторов на прирост выручки от продажи продукции в отчетном году необходимо принять величину прироста результативного показателя за 100% и относительно нее рассчитать удельный вес влияния каждого фактора.
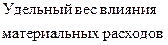 =
= 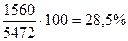
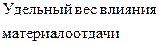 =
= 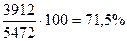
Как видно из расчетов, влияние второго фактора было наиболее существенным, что является положительным моментом, так как материалоотдача является интенсивным фактором, действие которого проявляется в повышении эффективности (отдачи) использования материальных ресурсов.
λМ, коэффициент
 |
Площадь бóльшего
 Прямоугольника ( ) = N отчетного года
Прямоугольника ( ) = N отчетного года

 72
72
 60
60
Площадь мéньшего прямоугольника =
= N предш..года
 0 300 326 М, тыс.руб.
0 300 326 М, тыс.руб.
Графическое изображение использования способа цепных подстановок
На рис. представлены графически: выручка от продажи продукции за отчетный год, объему которой соответствует площадь бóльшего прямоугольника (Nотч = 300 * 60 = 18000 тыс.руб.); выручка от продажи продукции за предшествующий год, объему которого соответствует площадь мéньшего прямоугольника (N = 326 * 72 = 23472 тыс.руб.). Разность между площадью большего и меньшего прямоугольников соответствует приросту выручки в отчетном году по сравнению с предшествующим годом. (ΔN = Nотч - Nпред= 23472 - 18000 = 5472 тыс.руб.). На рис.1.15 этот прирост выделен более интенсивным цветом. В соответствии с приведенными выше расчетами влияния факторов на прирост выручки от продажи продукции определено следующим образом:
ΔNR = Nскорр - Nпред = Мотч ∙ λМпред - Мпред ∙ λМпред = λМпред ∙ (Мотч - Мпред) =
= 60 ∙ (326 –300) = 1560 тыс.руб.
ΔN λ М = Nотч ∙ Nскорр = Мотч ∙ λМотч - Мотч∙ λМпред = Мотч ∙ (λМотч - λМпред) =
= 326 ∙ (72 – 60 ) = 3912 тыс.руб.
Последовательность замены значений факторов с предшествующих на отчетные установлена начиная с фактора материальных расходов (М). Если бы в первую очередь замены производились по фактору материалоотдачи (λМ), то результаты расчетов влияния факторов были бы другими. Такая ситуация объясняется наличием субъективизма при установлении последовательности замены значений факторов. Отсюда и основной недостаток способа цепных подстановок – проблема разложения дополнительного прироста выручки от продажи продукции, образующегося в результате одновременного действия двух факторов. На рис. 1.15 этот прирост занимает площадь правого верхнего квадрата. Данную проблему позволяет решить интегральный метод факторного анализа.
Интегральный метод, также как и способ цепных подстановок, применяется для измерения влияния факторов на результативный показатель в факторных моделях, отражающих функциональные зависимости. Он позволяет получить более точные результаты расчетов, не зависящие от последовательности замены базисных значений факторов на отчетные. Дополнительный прирост результативного показателя, образовавшийся от взаимодействия факторов, распределяется между ними.
Проблема разложения по факторам прироста результативного показателя, обусловленного их совместным влиянием, не может быть решена простым делением его на количество факторов, так как действие каждого отдельно взятого фактора отличается по величине, масштабности, направлению воздействия неоднозначно. В интегральном методе действует логарифмический закон перераспределения факторных нагрузок при соблюдении положения независимости факторов. Одной из особенностей интегрального метода факторного анализа является принцип общего подхода к решению самых разнообразных задач вне зависимости от количества факторов, включенных в модель, а также формы связи между ними. Для решения задач факторного анализа интегральным методом необходимо использовать различные формулы для измерения влияния факторов. Та или иная формула выбирается исходя из вида факторной системы (мультипликативная, кратная, смешанная). Сложность построения формул заключается в построении подынтегральных выражений элементов структуры факторной системы, так как этот процесс является индивидуальным для каждой конкретной факторной модели. В экономическом анализе разработаны формулы для измерения влияния факторов для наиболее часто встречающихся типов факторных систем, некоторые из них приведены в табл. 1.6. Использованы следующие обозначения: ¦ - результативные показатели; x , y, z – факторы; Аx, Аy, А z - влияние соответствующих факторов на результативные показатели.
Таблица 1.6
Формулы расчета влияния факторов на
результативный показатель
| Вид модели факторной системы | Ах | Ау | Аz |
| ¦=x∙y | Аx=1/2 Δx(y0+y1) | Аy=1/2 Δy(x0+x1) | - |
| ¦=x∙y∙z | Аx=1/2Δx(y0z1+ +y1z0)+1/3ΔxΔyΔz | Аy=1/2Δy (x0z1+x1z0)+ +1/3ΔxΔyΔz | Аz=1/2Δz(x0y1+ +x1y0)+1/3ΔxΔyΔz |
     x
¦=
y x
¦=
y
| Δ x y1 Аx= ln Δy y0 | Аy= Δ¦ - Ax | - |
       x
¦=
y + z x
¦=
y + z
| Δ x y1+z1 Аx= ln Δy+Δz y0+z0 | Δ¦ - Ax Аy= Δy Δy+Δz | Δ¦ - Ax Аy= Δz Δy+Δz |
Используя исходные данные табл. 1.5, можно произвести расчет влияния факторов интегральным методом, для этого необходимо ввести обозначения:
¦ 0 - выручка от продажи продукции предшествующего года;
¦ 1 - выручка от продажи продукции отчетного года;
x0 – материальные расходы предшествующего года;
x1 - материальные расходы отчетного года;
y0 - материалоотдача предшествующего года;
y1 – материалоотдача отчетного года.
Факторная зависимость описывается формулой: ¦=x ∙ y.
Влияние факторов на изменение выручки от продажи продукции в отчетном году рассчитывается по соответствующим формулам, приведенным в табл.1.6:
Аx=1/2 Δx(y0+y1) = ½ *(326 – 300) * (60 + 72) = 1716 (тыс.руб.)
Аy=1/2 Δy(x0+x1) = ½ * (72 – 60) * (300 + 326) = 3756 (тыс.руб.)
Совокупное влияние факторов, равное 5472 тыс.руб. (1716 + 3756), соответствует приращению результативного показателя 5472 тыс.руб. (23472 – 18000).
При сравнении результатов, полученных интегральным методом и методом цепных подстановок, обнаруживаются расхождения в значениях влияния факторов. В частности, по интегральному методу (более объективному) влияние материальных расходов оказалось на 156 тыс.руб. больше, чем по методу цепных подстановок, что объясняется перераспределением дополнительного прироста выручки от продажи продукции, связанного с совместным воздействием факторов на результативный показатель.
Дифференцирование так же является методом количественной оценки влияния отдельных факторов на изменение результативного показателя. При использовании этого метода предполагается, что приращение результативного показателя (функции) распределяется на слагаемые, каждое из которых определяется как произведение соответствующей частной производной на приращение переменной, по которой вычислена данная производная. Пусть имеется функция y = ƒ (x 1 , x 2), тогда ее полное приращение определяется следующим образом:
Δy= 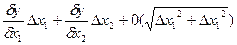
где Δy – приращение результативного показателя (функции);
Δx1 - приращение первого фактора;
Δx2 - приращение второго фактора;
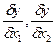 - частные производные;
- частные производные;
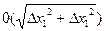 - бесконечно малая величина более высокого порядка , чем
- бесконечно малая величина более высокого порядка , чем 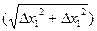 ;
;
Влияние факторов x1 и x2 на изменение y определяется так:
Δyх1= 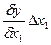
Δyх2= 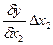
Сумма влияния факторов представляет собой главную часть приращения результативного показателя (Δy). Параметр 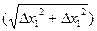 мал (достаточно близок к нулю) при малых изменениях факторов. Его значение может быть существенным (отличным от нуля) при больших изменениях факторов, что может привести к ошибкам в оценке влияния факторов.
мал (достаточно близок к нулю) при малых изменениях факторов. Его значение может быть существенным (отличным от нуля) при больших изменениях факторов, что может привести к ошибкам в оценке влияния факторов.
В качестве примера дифференцирования, как метода факторного анализа, можно рассмотреть конкретную задачу, в которой результативным показателем является выручка от продажи продукции (N), а факторами – материальные расходы (М) и материалоотдача ( 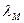 ). Взаимосвязь между факторами и результативным показателем выражается функцией N = М×λМ. Влияние факторов по методу дифференцирования рассчитывается следующим образом:
). Взаимосвязь между факторами и результативным показателем выражается функцией N = М×λМ. Влияние факторов по методу дифференцирования рассчитывается следующим образом:
ƒλ΄ΔλМ - влияние изменения материалоотдачи, где ƒλ΄ - частная производная функция по аргументу λМ;
ƒМ΄ΔМ - влияние изменения материальных расходов, где ƒМ΄ - частная производная функция по аргументу М.
Дата добавления: 2017-04-20; просмотров: 897;
