Классификация квадрик

Левую часть уравнения (1) путём известных методов (выделения полного квадрата, метод Лагранжа), как квадратичную форму можно свести к каноническому виду:

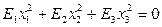где .

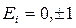В проективной системе координат сохраняется закон инерции.

Существует пять видов квадрик:

1.

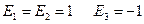
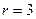
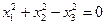- овальная квадрика

2.

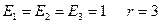
- нулевая квадрика

3.

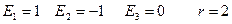
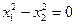- пара прямых

4.

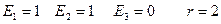
- пара мнимых прямых

5.

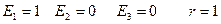
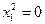- пара совпавших прямых

Классификация квадрик в проективной геометрии позволяет работать только с одной невырожденной квадрикой (овальной), которая не является нулевым множеством, в то время как в аффинной системе координат имеется три квадрики (эллипс, гипербола, парабола).

С учетом классификации квадрик на проективной плоскости можно составить более детальную классификацию на аффинной плоскости.

Ранг	Аффинный класс	Проективный класс
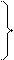	1. мнимый эллипс эллипс 2. парабола гипербола	1. нулевая квадрика   2. овальная квадрика
	1. пара мнимых пересекающихся прямых 2. пара мнимых параллельных прямых 3. пара параллельных прямых 4. пара пересекающихся прямых	пара мнимых прямых пара действительных прямых
	пара совпавших прямых	пара совпавших прямых