Мнимые точки проективной плоскости. Линии второго порядка на проективной плоскости. Проективная классификация линий второго порядка.

Если на проективной плоскости 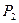задан проективный репер 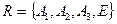, то любая точка плоскости имеет проективные координаты 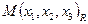, которые являются действительными числами, не равными нулю одновременно. Дополним проективную плоскость так называемыми мнимыми точками. Введем следующее соглашение: при выбранном репере 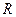точкой назовем любую тройку чисел 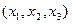, не равных одновременно нулю, взятых в определенном порядке. 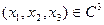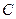Здесь , где - множество всех комплексных чисел, 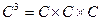. Числа 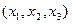- координаты точки. Точк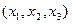и и 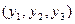совпадают тогда и только тогда, когда существует число 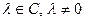, такое, что .

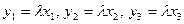Определение 7.1. Точка 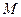называется вещественной, если ее координаты – вещественные числа или могут быть приведены к вещественным числам умножением на какое-то комплексное число 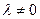; в противном случае точка называется мнимой.

Например, 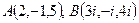- вещественные, 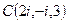- мнимая.

В дальнейшем будем рассматривать только такие реперы плоскости, для каждого из которых все вершины и единичная точка являются вещественными точками.

Определение 7.2. Множество всех вещественных и мнимых точек будем называть комплексной проективной плоскостью.

Определение 7.3. Две точк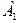и и 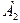называются комплексно-сопряженными точками, если их координаты могут быть записаны в виде 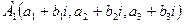и .

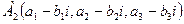Понятия мнимой точки и комплексно-сопряженных точек не зависит от выбора системы координат.

Определение 7.4. Прямой линией комплексной проективной плоскости называется множество всех (вещественных и мнимых) точек, координаты 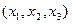при выбранном репере удовлетворяют уравнению: 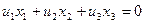, причем коэффициенты 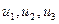(координаты прямой) – комплексные числа, которые не равны нулю соответственно.

Определение 7.5. Прямая называется вещественной, если ее координаты – вещественные числа или могут быть приведены к вещественным числам умножением на какое-то комплексное число 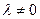; в противном случае прямая называется мнимой.

Справедливы следующие утверждения:

1. На каждой вещественной прямой лежит бесконечное множество мнимых точек.

2. На каждой мнимой прямой лежит одна вещественная точка.

3. Через две точки проходит одна и только одна прямая. Через комплексно-сопряженные точки проходит вещественная прямая.

4. Любые две прямые пересекаются в одной точке (вещественной или мнимой).

Пусть на проективной плоскости 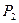задан проективный репер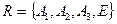

Определение 7.6. Множество точек проективной плоскости, координаты которых в проективной системе координат удовлетворяют уравнению второй степени 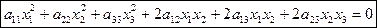(1), называется квадрикой или линией второго порядка.

Коэффициенты 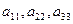- действительные числа, не равные нулю одновременно, причем 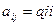. Матрица 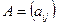- симметрическая.

Левая часть уравнения - однородный многочлен второй степени (вместе с тройкой чисел 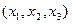уравнению удовлетворяет и весь класс пропорциональных троек), который представляет собой квадратичную форму.

Определение квадрики в проективной системе координат не зависит от выбора системы координат.

Каждая квадрика характеризуется рангом, который определяется рангом соответствующей квадратичной формы.

Определение 7.7. Рангом квадратичной формы называется ранг соответствующей ей матрицы.

Определение 7.8. Линия называется невырожденной, если ранг равен трём, вырожденной, если ранг меньше трёх.

Понятие линии второго порядка и её ранга являются проективными понятиями, то есть не меняются при различных проективных преобразованиях.

Теорема 7.9. Любая прямая пересекает невырожденную линию второго порядка не более чем в двух точках.

Доказательство методом от противного.

1. Предположим, что прямая 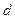пересекает квадрику 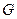более чем в двух точках: , ,

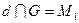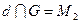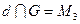
2. Докажем противоречие условию:

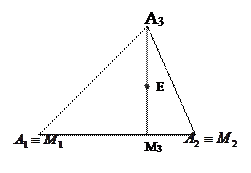· Введём произвольный репер, так что

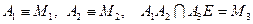, тогда

, ,

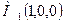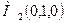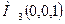
· Подставим координаты точек 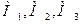в общее уравнение квадрики. Имеем: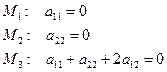

Матрица квадратичной формы примет вид: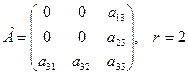

· По определению 7.8 имеем, что данная по условию квадрика является вырожденной. Получили противоречие с условием.

3. Значит, прямая пересекает невырожденную линию второго порядка не более чем в двух точках