Гармонические четверки
Пусть точки А,В,С,D принадлежат одной прямой. Говорят, что пара СD разделяет пару АВ, если их сложное отношение меньше 0, в противном случае пара СD не разделяет пару АВ.
Понятие разделенности не зависит от порядка рассмотрения пар АВ и СD и от порядка рассмотрения точек А,В,С,D.
Определение 4.5. Четверка точек А,В,С,D называется гармонической, если сложное отношение 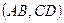 равно -1.
равно -1.
Свойства гармонической четверки
1) В гармонической четверке пары разделяют друг друга;
2) Гармонизм точек не нарушается при таких перестановках, которые не меняют состава пар.
Теорема 4.6. Для того чтобы четверка точек расширенной евклидовой прямой, содержащая одну несобственную точку и три собственных, была гармонической необходимо и достаточно, чтобы точка, находящаяся в паре с несобственной, была серединой отрезка, образованного другими двумя собственными точками.
Доказательство
(1) ( 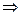 )Пусть
)Пусть 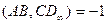 . Докажем, что точка С – является серединой AB. По теореме 4.4. имеем:
. Докажем, что точка С – является серединой AB. По теореме 4.4. имеем: 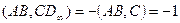 ,
, 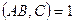 или
или 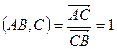
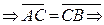 C- середина;
C- середина;
(2) ( 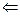 ) Доказывается в зависимости от расположения несобственной точки.
) Доказывается в зависимости от расположения несобственной точки.
Пусть А – несобственная точка, тогда В - середина CD. По свойствам сложных отношений имеем: 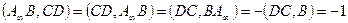
 Определение 4.7. Сложным отношением четырёх прямых пучка называется число равное отношению двух отношений
Определение 4.7. Сложным отношением четырёх прямых пучка называется число равное отношению двух отношений 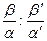 , где
, где 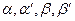 действительные числа, такие что
действительные числа, такие что 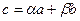 и
и 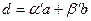 .
.
Теорема 4.8. Пусть 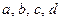 - различные прямые, принадлежащие пучку. A,B,C,D – четыре точки, инцидентные одной прямой, не проходящей через центр пучка, образованные при пересечении прямых a,b,c,d и данной прямой.
- различные прямые, принадлежащие пучку. A,B,C,D – четыре точки, инцидентные одной прямой, не проходящей через центр пучка, образованные при пересечении прямых a,b,c,d и данной прямой.
Тогда сложное отношение четырёх точек равно сложному отношению четырёх прямых (AB,CD)= (ab,cd).
Доказательство
1. Условие принадлежности точки прямой можно записать в матричном виде
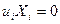 или
или 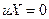
· точка 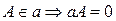
· точка 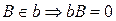
· точка 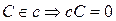
· точка 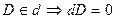
2. По определению сложного отношения прямых и точек имеем:
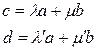
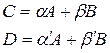
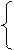 3. Подставим в условие принадлежности полученные равенства:
3. Подставим в условие принадлежности полученные равенства:
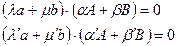
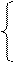


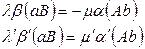
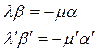
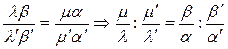
Ч.т.д.
Свойства сложного отношения точек и прямых
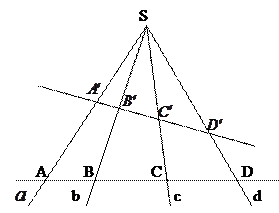 Утверждение 4.9.
Утверждение 4.9.
Если четыре прямых пучка пересечены двумя прямыми, то на этих прямых получаются четвёрки точек, имеющих равные двойные отношения: 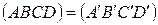
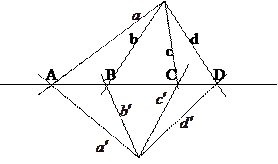 Утверждение 4.10
Утверждение 4.10
Если четыре точки, лежащие на одной прямой инцидентны четырём прямым одного пучка и четырем прямым другого пучка, то двойные отношения четвёрок прямых равны
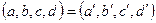

Дата добавления: 2017-01-29; просмотров: 1749;
