Свойства сложного отношения четырех точек
1) Сложное отношение четырех точек прямой не зависит от выбора проективного репера на прямой;
2) Сложное отношение четырех точек прямой не зависит от выбора координатных столбцов из класса пропорциональных столбцов;
3) При перестановке пар точек сложное отношение не меняется 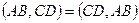 ;
;
4) При перестановке точек одной пары сложное отношение меняется на обратное 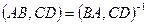 ,
,  ;
;
5) При перестановке точек двух пар сложное отношение не изменяется (AB,CD)=(BA,DC);
6) если в четверке есть одинаковые точки, то сложное отношение определяется:
D=C 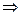 (AB,CC)=1; D=B
(AB,CC)=1; D=B 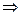 (AB,CD)=0; D=A
(AB,CD)=0; D=A 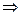 (AB,CA)=
(AB,CA)= 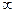
7) при перестановке крайних (средних) точек, сложное отношение меняется на дополнительное при единице: (AB,CD)=1- (DB,CA)=1-(AC,BD).
Теорема 4.3. (существование и единственность точки, находящейся с данными тремя точками в сложном отношении)
Если A,B,C – различные точки, а  - действительное число, то на данной прямой существует одна и только одна точка Х, такая, что
- действительное число, то на данной прямой существует одна и только одна точка Х, такая, что 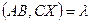 .
.
Доказательство
1.Существование. Рассмотрим проективный репер R=(A,B,C,) и точку X в этом репере. По замечанию 4.1.1. к определению 4.1 точка Х имеет координаты 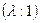 . Значит,
. Значит, 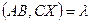 .
.
2. Единственность. Предположим, что точка Х’(х1,х2) и сложное отношение 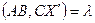 . По замечанию к определению 4.1
. По замечанию к определению 4.1 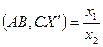 . Значит,
. Значит, 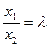 или
или 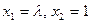 , т.е.
, т.е. 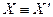 .
.
Следствие: Если на прямой даны точки А,В,С,D и А’,В’,С’,D’ , причем сложное отношение этих четверок совпадает, то 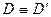 .
.
Теорема 4.4. (геометрический смысл сложного отношения 4-х точек на расширенной прямой)
Если точки А,В,С,D - собственные точки расширенной прямой, а 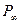
 - несобственная точка расширенной прямой, то сложное отношение точек)=
- несобственная точка расширенной прямой, то сложное отношение точек)= 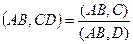 ;
; 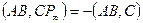 .
.
Доказательство
1. Рассмотрим проективный репер, образованный точками 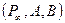 . Тогда в нем
. Тогда в нем 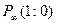 , А(0,1),В(1,1). Пусть С(с1,с2), D(d1,d2).
, А(0,1),В(1,1). Пусть С(с1,с2), D(d1,d2).
2. По формуле нахождения сложного отношения найдем:
(1) 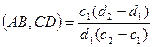
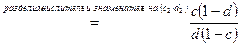
(2) 
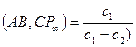
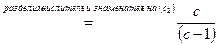
3. Выразим простые отношения данные в условии. Для этого определим координаты А,В,С,D в системе 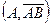 :
: 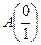 ,
,  . Имеем, что А(0), В(1), С(с), D(d), где
. Имеем, что А(0), В(1), С(с), D(d), где 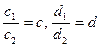 .
.
По формуле простого отношения 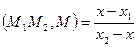 находим
находим 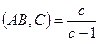 и
и 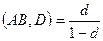 .
.
4. Подставив получившиеся равенства в условие теоремы, легко доказывается истинность равенств 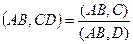 и
и 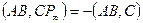 .
.
Дата добавления: 2017-01-29; просмотров: 2369;
