Случайная вариация и ее закономерности

Вероятность- это возможность осуществления того или иного события в некотором количестве случаев из общего числа возможных.

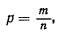
, где p – это вероятность, m- число благоприятных случаев, n – число всех возможных случаев.

Примером является рождение самцов и самок в популяции. Вероятность проявления того или иного генетического заболевания 1 на 10000 человек.

Заключение: количественной характеристикой вероятности того или иного явления т.е. объективным мерилом, по которому можно судить о возможности возникновения явления в будущем, может быть относительная частота явления, установленная на большом фактическом материале.

По мере приближения р к единице события становятся все более достоверными.

Закономерности случайной вариации:

1. теорема сложения вероятностей: относится к независимым друг от друга событиям, которые несовместимы.

2. теорема умножения вероятностей, относится к независимым событиям, которые совместимы друг и другом или следует друг за другом.

Первый пример: на клумбах растут 10 белых, 40 красных и 25 синих астр. Какова вероятность в темноте сорвать окрашенную астру?

Какова вероятность наличия цифры 4 наверху двух выброшенных кубиков? Вероятность для 1 кубика равна 1/6, для 2 кубиков – 1/6*1/6=1/36.

Количество случаев рождения ребенка с Синдромом Дауна в зависимости от возраста матери:

Возраст матери на момент родов	Риск синдрома Дауна
15 или меньше	1:720
	1:800
	1:900
	1:1030
	1:1200
	1:1200
	1:1200
	1:1030
	1:1030
	1:900
	1:900
	1:850
	1:800
	1:760
	1:720
	1:690
	1:650
	1:550
	1:440
	1:360
	1:280
	1:210
	1:160
	1:130
	1:100
	1:75
	1:60
	1:45
	1:35
	1:30
	1: 21
	1:17
	1:13
	1:8

Это называется теоретической вероятностью. Эмпирическая вероятность – вычисленная опытным путем.

Распределения вероятностей:

Подкидываем две монеты одновременно - 4 случая:

1. монеты падают орлами вверх ОО

2. выпадает ОР

3. Выпадает РО

4. Выпадает РР.

Вероятность выпадения двух орлов равна произведению вероятностей : рр, двух решек – gg или q² . Следующие вероятности pq+pq=2pq.

(p+q)²=p²+2pq+q².

Во всех случаях получение вероятностей различных сочетаний независимых событий основывается на том, что вероятности нескольких комбинаций выражаются членами разложения бинома, где (p+q)k, где k – число независимых случайных событий, p и q – вероятности благоприятных и неблагоприятных событий.

Разложение бинома Ньютона:

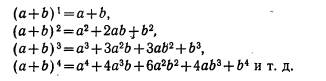
Для получения коэффициентов используется треугольник Паскаля:

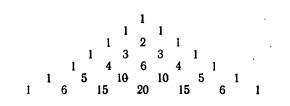
Биномиальное распределение – это вероятности появления отдельных значений xi, выражающиеся величинами, соответствующие коэффициентам разложения бинома Ньютона. Биномиальное распределение относится к прерывным (дискретным).

Средняя арифметическая при биномиальном распределении равна:

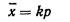
, а среднее квадратическое отклонение:

<== предыдущая лекция	\|	следующая лекция ==>
Проблемы развития элементной базы	\|	ОСОБЕННОСТИ МАССАЖА И ЗАНЯТИЙ ФИЗИЧЕСКИМИ УПРАЖНЕНИЯМИ ВО ВРЕМЯ БЕРЕМЕННОСТИ, В РОДАХ И ПОСЛЕРОДОВОМ ПЕРИОДЕ.

Дата добавления: 2017-01-29; просмотров: 874;