Задача Эйлера устойчивость упругого стержня
Исторически первые работы по устойчивости упругого стержня были написаны российским ученым швейцарского происхождения Леонардом Эйлером (1707-1783). Рассмотрим его решение задачи устойчивости упругого стержня, постоянного поперечного сечения. Стержень, расположен на двух шарнирно опертых концах, при действии продольной силы переменной величины Р (рис.62). Впервые эта задача была поставлена и решена Л. Эйлером в середине XVIII века.
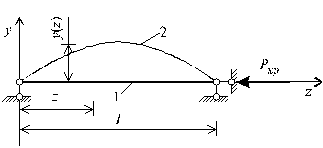
Рис.62 Расчетная схема стержня нагруженного продольной силой
На начальном этапе действия постоянно возрастающей силы Р, очевидно, что в поперечных сечениях стержня возникают только продольно сжимающие силы и стержень испытывает сжатие, сохраняя прямолинейную форму деформированного состояния (1). Считая данную форму деформированного состояния в качестве начальной, предполагают, что при некотором значении внешней силы Р=Pкр стержень изогнется, т.е. в некотором новом равновесном состоянии принимает искривленную форму (2), изображенную на рис.62.
Обозначая величину прогибов стержня через y (z) в сечении, расположенном на расстоянии z от начала системы координат y z, значения изгибающих моментов в указанном поперечном сечении от действия внешней силы Р принимают значения 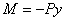 .
.
Из теории изгиба, при малых прогибах и пренебрегая продольными деформациями, деформированное состояние стержня за счет изгиба, описывается уравнением
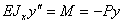 . (113)
. (113)
Принимая обозначение
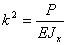 (114)
(114)
уравнение (113) можно представить в следующем виде:
 (115)
(115)
Решение (115) имеет следующий вид:
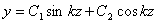 (116)
(116)
Произвольные постоянные С1 и С2 определяются из граничных условий закрепления балки, т.е.y(0) = 0; y(l) = 0.
Из первого условия вытекает, что С2 = 0, а из второго
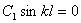 (117)
(117)
Последнее уравнение имеет два возможных решения: либо С1 = 0, либо же C2 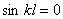 .
.
В первом случае получается, чтоС1 =С2 =0 и перемещения согласно (116) тождественно равны нулю, т.е. y = 0. Это решение очевидно соответствует первоначальному равновесному состоянию, которое нас не интересует. Во втором случае, т.е. предполагая, что С1 ¹ 0, из (115) следует, что 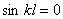 . Откуда следует, что
. Откуда следует, что 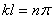 , где n = 1,2,3,... С учетом выражения (114), получим
, где n = 1,2,3,... С учетом выражения (114), получим 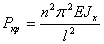 . Наименьшая критическая сила
. Наименьшая критическая сила 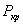 получается при n=1:
получается при n=1:
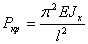 (118)
(118)
Эта сила носит название первой критической или Эйлеровой силы. Решение (115) при С1 = 0 и C2=0 принимает вид Y=C1sin((nπz)/l).
При выполнении практических расчетов, как правило, определяется критическое значение внешней силы, соответствующее низшей форме потери устойчивости системы. Поэтому мы далее будем рассматривать решение задачи по определению только наименьшего значения критических сил.
Основные теоремы при продольно-поперечном изгибе
Теорема о взаимности работ
Если одна и та же система находится в двух напряженных состояниях под действием одинаковых продольных нагрузок, но произвольных внешних поперечных сил (рис.63), то возможная работа поперечных сил 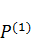 первого состояния на соответствующих перемещениях второго состояния равна возможной работе поперечных сил
первого состояния на соответствующих перемещениях второго состояния равна возможной работе поперечных сил 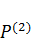 второго состояния на соответствующих перемещениях, вызванных силами первого состояния:
второго состояния на соответствующих перемещениях, вызванных силами первого состояния: 
или 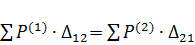 (119)
(119)
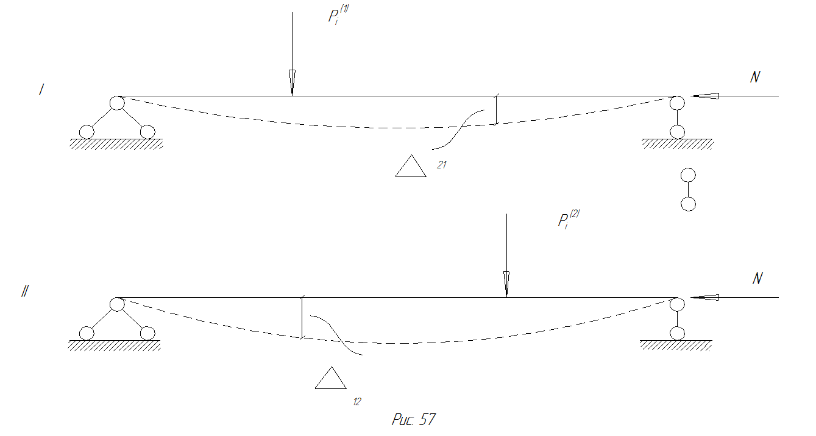
Рис. 63 Рисунок к теореме о взаимности работ.
Если одна и та же система находится в двух напряженных состояниях под действием одинаковых продольных нагрузок, но произвольных единичных поперечных сил (рис.63), то единичное перемещение 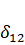 по направлению силы
по направлению силы 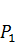 от силы
от силы 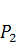 равно единичному перемещению
равно единичному перемещению 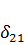 по направлению силы
по направлению силы 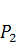 от силы
от силы 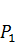 .
.
Теорема о взаимности перемещений является частным случаем теоремы о взаимности работ ( 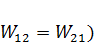 .Так как
.Так как 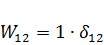 и
и 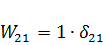 ,
,
то 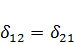 (119)
(119)

Рис. 64 Рисунок к теореме о взаимности перемещений.
Если система находится в двух состояниях, характеризуемых одинаковыми продольными нагрузками (рис. 65), то для этих состояний применима теорема о взаимности реакций: реакция связи К от единичного смещения связи i равна реакции связи i от единичного смещения связи К, т.е. 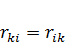 (120)
(120) 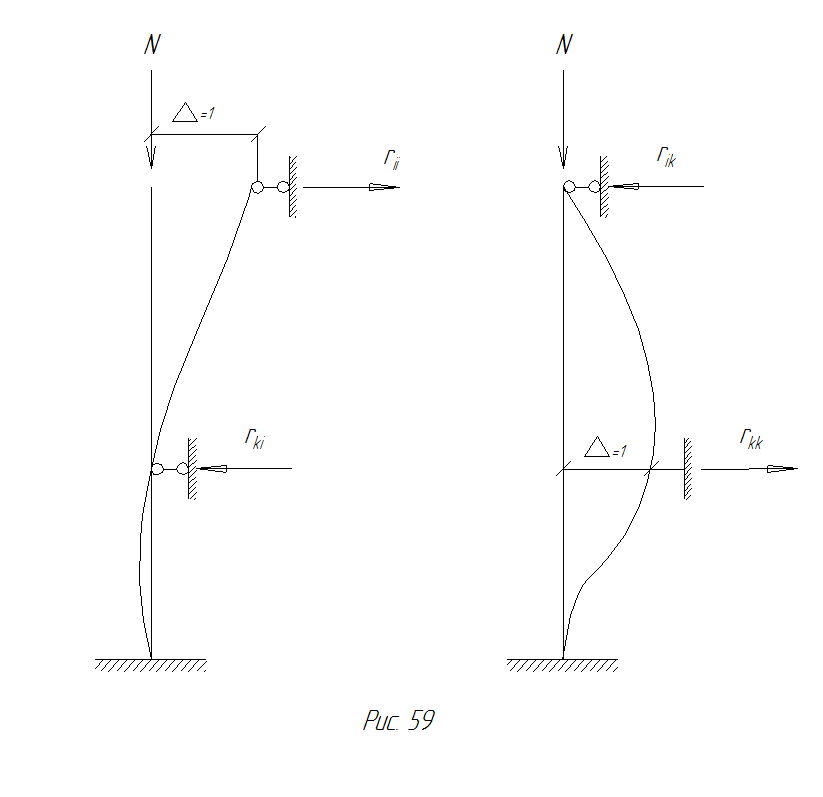
Рис. 65 Рисунок к теореме о взаимности реакций.
Подсчитаем возможные работы:

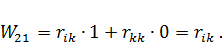
Так как 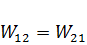 , то
, то 
| <== предыдущая лекция | | | следующая лекция ==> |
| Виды теплоизоляционных материалов холодильников | | | Проведение предварительной патентной экспертизы |
Дата добавления: 2017-01-29; просмотров: 2057;
