Синусоидалы функцияларды айнымалы векторлардың проекциялары түрінде көрсету
Электр тізбек күрделенгенде тригонометриялық түрде есептеу қиындап кетеді, ал сол себептен тұрақты тоқ тізбектерге ұқсасты айнымалы тоқ тізбектерді алгебралық түрде есептеуге рұқсат ететін әдіс керек болады. Мұндай ыңғайлы әдіс ретінде синусойдалы функцияларды құрауды айнымалы векторларды қарауға ауыстыруға орнатылған комплексті әдіс.
Комплексті жазықтықта әрбір нүкте бұл нүктені радиус-векторымен белгіленеді. Вектордың басы координат басымен үйлеседі, ал аяғы берілген комплексті санға сәйкесті нүктеде жатады (2.5-сурет).
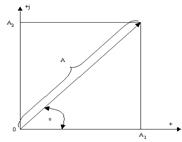
2.5-сурет. Комплексті санды бейнейлейтін вектор.
Комплексті санды көрсеткіш немесе полярлы түрде жазуға болады: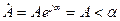 
мұнда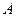 
-модуль; 
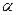-аргумент немесе фаза;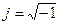 
Комплексті санның тригонометриялық түрде жазылуы:
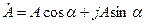
және оның алгебралық түрі:
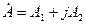
мұнда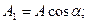 
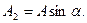
Демек,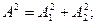 
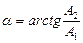
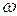бұрыштық жылдамдықпен болымды бағытпен, яғни сағат тіліне қарсы, айналып тұрған векторды былай көрсетуге болады:
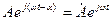
мұнда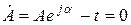 
уақыт мезгілде векторды көрсететін комплекстіамплитуда (2.6-сурет). Басқаша айтқанда, бұл уақыттан тәуелсіз, модуль және аргументы берілген синусоидалды функцияның амплитудасына және басты фазасына тең комплексті шама.
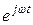көбейткіш – айналдыру оператор. Комплексті амплитуда 
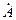-ны 
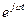көбейту болымды бағытқа вектор 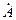-ны бұрыш 
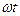бұруды көрсетеді.
 |
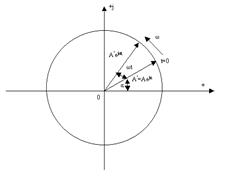2.6-сурет. Айналмалы вектор.
тригонометриялық түрде жазғанда шығады:
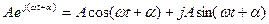
Фаза бойынша олардың өзара бағытта болуды сақтаумен құрылған векторлардың жиынтықтарын бейнелейтін диаграмма векторлық диаграмма деп аталады.
Дата добавления: 2017-01-29; просмотров: 1313;