Кинетика Михаэлиса – Ментен

Предварительные эксперименты по изучению кинетики ферментативных реакций показали, что скорость реакции 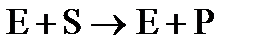, вопреки теоретическим ожиданиям, не зависит от концентрации фермента (Е) и субстрата (S) таким образом, как в случае обычной реакции второго порядка.

Браун и независимо от него Анри впервые выдвинули гипотезу об образовании в ходе реакции фермент-субстратного комплекса. Затем это предположение подтвердили три экспериментальных факта:

а) папаин образовывал нерастворимое соединение с фибрином (Вюртц, 1880);

б) субстрат инвертазы сахароза могла защищать фермент от тепловой денатурации (О'Салливан и Томпсон, 1890);

в) было показано, что ферменты являются стереохимически специфическими катализаторами (Фишер, 1898–1899).

В 1913 г. Михаэлис и Ментен опубликовали свою теорию общего механизма ферментативных реакций:

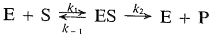
Они ввели понятие максимальной скорости и показали, что кривая насыщения (т.е. зависимость скорости реакции от концентрации субстрата) является равнобочной гиперболой. Они доказали, что максимально наблюдаемая скорость есть одна из асимптот к кривой, а отрезок, отсекаемый на оси абсцисс (в области ее отрицательных значений) второй асимптотой, т.е. константа в уравнении скорости, равен по абсолютному значению концентрации субстрата, необходимой для достижения половины максимальной скорости.[2]

Михаэлис и Ментен предположили, что скорость реакции определяется распадом комплекса ES, т.е. константой k₂. Это возможно только при условии, что k₂– наименьшая из констант скорости. В этом случае равновесие между фермент-субстратным комплексом, свободным ферментом и субстратом устанавливается быстро по сравнению со скоростью реакции (быстро устанавливающееся равновесие).

Начальную скорость реакции можно выразить следующей формулой:

v = k₂ [ES]

Поскольку константа диссоциации фермент-субстратного комплекса равна

K_S = [E] [S] / [ES] = k _-1/k₁

то концентрацию свободного фермента можно выразить как

[E] =K_S [ES] / [S]

Общая концентрация фермента в реакционной смеси определяется формулой

[Е]_т = [Е] + [ЕS] = K_S [ЕS] / [S] + [ЕS]

Реакция достигает максимальной скорости, когда концентрация субстрата достаточно высока, чтобы все молекулы фермента находились в виде комплекса ЕS (бесконечно большой избыток субстрата). Отношение начальной скорости к теоретически возможной максимальной скорости равно отношению [ЕS] к [Е]_т:

v / V_max= [ES] / [E]_т= [ES] / (K_S [ES] / [S] + [ES]) = 1 / (K_S+[S] +1)

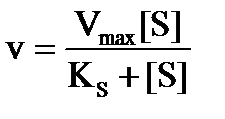
Это классическое уравнение Михаэлиса и Ментен, которое со времени его публикации в 1913 г. стало фундаментальным принципом всех кинетических исследований ферментов в течение десятилетий и с некоторыми ограничениями осталось таким до сих пор. [5]

Позднее было показано, что оригинальное уравнение Михаэлиса – Ментен предполагало наличие нескольких ограничений. Оно справедливо, т.е. правильно описывает кинетику реакции, катализируемой данным ферментом, только при условии выполнения всех следующих ограничительных условий:

1) образуется кинетически устойчивый фермент-субстратный комплекс;

2) константа K_Sявляется константой диссоциации фермент-субстратного комплекса: это справедливо, только если ;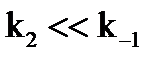

3) концентрация субстрата не меняется в ходе реакции, т.е. концентрация свободного субстрата равна его начальной концентрации;

4) продукт реакции быстро отщепляется от фермента, т.е. не образуется кинетически значимого количества ЕS комплекса;

5) вторая стадия реакции необратима; точнее говоря, мы принимаем во внимание только начальную скорость, когда обратной реакцией (из-за фактического отсутствия продукта) еще можно пренебречь;

6) с каждым активным центром фермента связывается только одна молекула субстрата;

7) для всех реагирующих веществ вместо активностей можно использовать их концентрации. [2]

Уравнение Михаэлиса – Ментен служит отправной точкой при любом количественном описании действия ферментов. Следует подчеркнуть, что кинетическое поведение большинства ферментов значительно сложнее, чем это вытекает из идеализированной схемы, лежащей в основе уравнения Михаэлиса – Ментен. При выводе этого уравнения предполагается, что существует только один фермент-субстратный комплекс. Между тем в действительности в большинстве ферментативных реакций образуется, по меньшей мере, два или три таких комплекса, возникающих в определенной последовательности.

Здесь через EZ обозначен комплекс, соответствующий истинному переходному состоянию, а через ЕР – комплекс между ферментом и продуктом реакции. Можно указать также, что в большинстве ферментативных реакций участвует более одного субстрата и образуется соответственно два или большее число продуктов. В реакции с двумя субстратами, S₁ и S₂, может образоваться три фермент-субстратных комплекса, а именно ES₁, ES₂ и ES₁S₂. Если в результате реакции получается два продукта, P₁ и P₂, то может существовать, по меньшей мере, еще три дополнительных комплекса EP₁, EP₂ и EP₁P₂. В таких реакциях имеется много промежуточных стадий, каждая из которых характеризуется своей константой скорости. Кинетический анализ ферментативных реакций, в которых принимают участие два реагирующих вещества или более, часто оказывается исключительно сложным и требует использования электронных вычислительных машин. Тем не менее, при анализе кинетики всех ферментативных реакций отправной точкой всегда является рассмотренное выше уравнение Михаэлиса – Ментен. [5]