Визначення нормальних напружень при згинанні
При прямому поперечному згинанні у поперечному перерізі балки виникають два внутрішніх зусилля Q та М; залежності між цим зусиллям та напруженнями у поперечному перерізі балки такі:
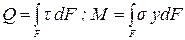 .
.
Отже, в поперечних перерізах балки при згинанні виникають як дотичні напруження так і нормальні напруження. Дотичні напруження при згинанні балок у переважній більшості випадків не враховуються. Особливі випадки коли величиною дотичних напружень знехтувати не можливо, тут не розглядаються.
Статична сторона задачі
Для виводу формул, що визначають нормальні напруження, які виникають в поперечному перерізі балки, розглянемо балку, що знаходиться в умовах чистого згину (рис. 6.13), тобто Q = 0 і дотичні напруження відсутні. Двома нескінченно близькими поперечними перерізами виділимо з цієї балки елемент довжиною dx (рис. 6.13,а).
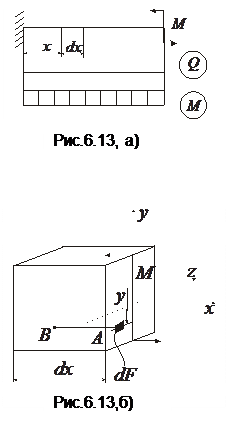
Переріз балки прямокутник. В площині перерізу проведемо координатні осі (рис.6.13,б).
Приймаємо, що вісь збігається з силовою лінією (лінію перетину силової площини з площиною перерізу); вісь z проведемо перпендикулярно осі у ; вісь х направлена перпендикулярно до площини перерізу. У перерізі виділимо елемент з площею dF (точка А), його координати – у, z. При чистому згинанні (Q=0, ) на елемент діє зусилля dN = sdF. Тоді з шести інтегральних рівнянь можна використати три:
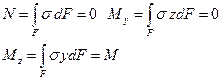
Але цих трьох рівнянь статики не достатньо для визначення s , тому що невідомий закон розподілу σ по перерізу та розташування осі Z.
Геометрична сторона задачі
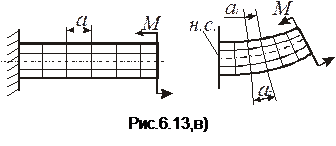
Розглянемо картину деформацій цієї балки. Якщо на еластичну балку нанести сітку з ліній паралельних і перпендикулярних осей, то при чистому згинанні прямокутна сітка деформується так що:
1) поздовжні лінії викривлюються по дузі кола;
2) поперечні лінії лишаються прямими і нахиляються одна до одної;
3) поперечні лінії з поздовжніми перетинаються під прямим кутом (рис. 6.13,в).
 |
На основі такої картини можна вважати, що при чистому згині поперечні перерізи лишаються плоскими і повертаються, лишаючись перпендикулярними до осі балки , тобто при чистому згинанні справедлива гіпотеза плоских перерізів.
Можна вважати, що відстань а між поперечними перерізами змінюється а1 < a, a2 > a , а саме верхні волокна скорочуються, а нижні – витягуються. Очевидно, що серед них є такі волокна які не змінюють своєї довжини. Сукупність таких волокон називають нейтральним шаром (рис. 6.13). Лінія перетину нейтрального шару із площиною поперечного перерізу балки називається нейтральною лінією Будемо вважати вісь z нейтральною віссю. Беручи до уваги картину деформацій, зобразимо деформований стан елемента dx ( рис. 6.14).
 Виділимо елемент балки двома суміжними поперечними перерізами m – m та n – n, які розташовані один від одного на відстані dx.
Виділимо елемент балки двома суміжними поперечними перерізами m – m та n – n, які розташовані один від одного на відстані dx.
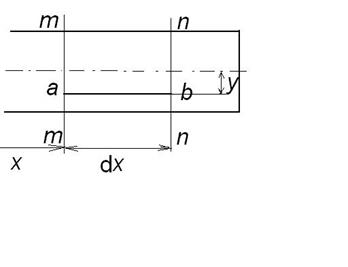
Розглянемо тепер цей елемент після деформування :
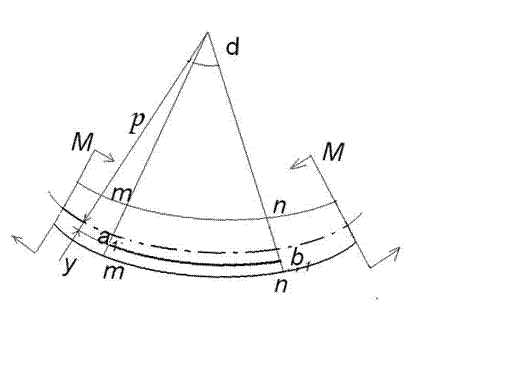
Н.С.
 - радіус кривизни.
- радіус кривизни.
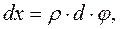
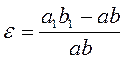
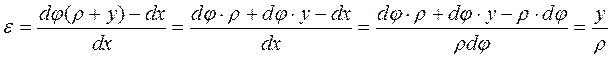
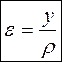
Фізична сторона задачі.
На елементарній площадці дотичних напружень немає. Волокна матеріалу не тиснуть одне на одне. Таким чином волокно a b перебуває в лінійному напруженому стані:
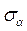
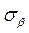
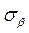
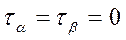 ;
; 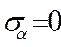
/ \
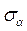
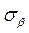 дотичних волокна не
дотичних волокна не
напружень тиснуть одне
нема на одне
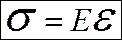
Синтез:
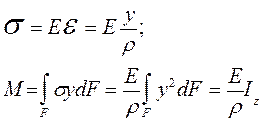
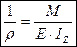 - закон Гука при згині;
- закон Гука при згині; 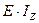 (добуток) – називається жорсткістю перерізу при згині
(добуток) – називається жорсткістю перерізу при згині 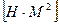
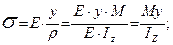
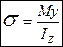 - формула Нав’є.
- формула Нав’є.
Формула Нав’є показує, що при згині нормальні напруження розподіляються за лінійним законом.
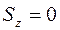 - Показує, що центр ваги лежить на осі Z.
- Показує, що центр ваги лежить на осі Z.
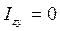 - Показує, що вісі Z та y головні центральні. Тобто вісь Z нейтральна лінія перерізу проходить через центр ваги, а осі y та z – головні центральні осі перерізу.
- Показує, що вісі Z та y головні центральні. Тобто вісь Z нейтральна лінія перерізу проходить через центр ваги, а осі y та z – головні центральні осі перерізу.
Тобто вісь z – нейтральна лінія перелізу проходить через центр вала, а вісі у та z – головні центральні вісі перелізу. Формула Нав’є показує, що незалежно від формі та розмірів перерізу балки, напруження в точках нейтральної лінії завжди дорівнюють 0. Величина 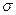 змінюється лінійно по товщині балки.
змінюється лінійно по товщині балки.
 |
Максимальні напруження
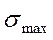 мають місце в найбільш віддалених від нейтральної лінії волокнах. У випадку симетричного перерізу:
мають місце в найбільш віддалених від нейтральної лінії волокнах. У випадку симетричного перерізу:
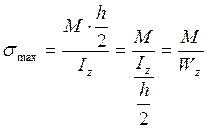
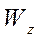 - осьовий момент опору
- осьовий момент опору 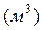
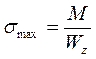 де
де 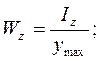
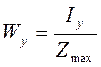
осьові моменти опору
Якщо переріз балки не має горизонтальної осі симетрії, то нейтральна лінія зміщена відносно середини висоти перерізу, але знову
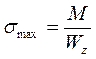 ; де
; де 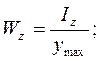
Для простіших перерізів:
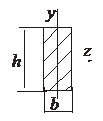 Прямокутник:
Прямокутник:
Wz = 2Iz/h = bh32/12h = bh2/6(6-5)
Wy = Iy2/b = hb2/6
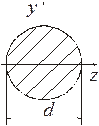
 Коло:
Коло:
Wy = Wz = 2Iocн/d = 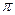 d4/64d =
d4/64d = 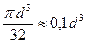 (6-6)
(6-6)
Кільце:
Wz = Wy = 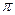 D3 (1-α4 )/32, (6-7)
D3 (1-α4 )/32, (6-7)
де α = d/D – відношення внутрішнього до зовнішнього
діаметра кільця.
Для прямокутного перерізу

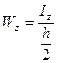
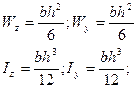
Для кругового
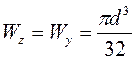
Для кільцевого 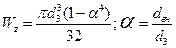
Для прокатних профілів значення Wz та Wy вказані у таблицях
Якщо переріз складний то визначаємо 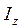 . Далі знаходимо
. Далі знаходимо 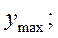 потім
потім 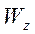 .
.
Затрати матеріалу пропорційна площі поперечного перерізу F. Отже чим більше відношення W/F, тим більший згинальний момент витримує переріз заданою площею.
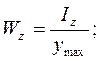 тобто переріз має бути розташованим так, щоб осьовий момент інерції був найбільший.
тобто переріз має бути розташованим так, щоб осьовий момент інерції був найбільший.
Умова міцності для нормальних напружень:
Тепер можна записати умову міцності для нормальних напружень при згинанні:
smax = Mmax/Wz ≤ [s] (6-8)
Умова міцності при згинанні дозволяє виконувати три типи розрахунків: перевірочний, проектувальний та визначення допустимого навантаження. Значення [s] береться те ж, що і при розтяганні – стисканні; Мmax – у небезпечному перерізі за епюрою згинального моменту.
Якщо розглядаються балки з пластичного матеріалу, не має різниці для яких волокон записати умову міцності – стиснутих або розтягнених, для пластичних матеріалів [s+] = [s -] .
Дата добавления: 2017-01-13; просмотров: 2036;
